Série d'exercices Mise en équations - équation problème - 2nd
Classe:
Seconde
Équation Problème
Exercice 1
Un cadet de Gascogne dit à ses amis : "J'ai dépensé 5 écus de plus que les deux neuvièmes du contenu de ma bourse et il me reste $2$ écus de moins que les deux tiers de ce que j'avais en rentrant dans cette taverne".
Combien avait-il d'écus dans sa bourse en rentrant ?
Exercice 2
Un cycliste effectue un parcours en $9$ heures. Sa vitesse est de $30\ km/h$ sur le premier tiers de la distance totale, $20\ km/h$ sur le second tiers et 15 km/h sur le troisième tiers.
Trouver la distance parcourue.
Exercice 3
Trouver trois nombres entiers consécutifs tels que la différence entre le carré du plus grand et le produit des deux autres soit égale à $715.$ (on pourra noter ces nombres $x$, $x+1$ et $x+2$)
Exercice 4
A $9$ heures du matin Paul part de $A$ vers $B$ en bicyclette $($vitesse $15\ km/h).$ A $10$ heures moins le quart, Pauline en fait autant de $B$ vers $A$ $($vitesse $20\ km/h).$ Ils se rencontrent à mi-chemin pour pique-nique.
Quelle heure est-il alors ?
Exercice 5
Valérie et Maria doivent parcourir $30\ km$ chacune. Valérie met $3\;h$ de plus que Maria. Si elle doublait sa vitesse, elle mettrait $2\;h$ de moins.
Quelle est la vitesse de chacune.
Exercice 6
"Un homme est entré dans un verger et a cueilli des fruits. Mais le verger avait trois portes et chacune était gardé par un gardien. Cet homme donc partagea en deux ses fruits avec le premier et lui en donne deux de plus ; puis il partagea le reste avec le second et lui en donne deux de plus, enfin il fit de même avec le troisième. Il sortit du jardin avec un seul fruit.
Combien en avait-il cueilli ?
Exercice 7
On veut disposer un certain nombre de jetons en carré $($par exemple avec $9$ jetons on fait un carré de $3$ sur $3).$ En essayant de constituer un premier carré, on s'aperçoit qu'il reste $14$ jetons. On essaie alors de faire un deuxième carré en mettant un jeton de plus par côté. Il manque alors $11$ jetons.
Combien y avait-il de jetons au départ ?
Exercice 8
Une somme de $3795\ F$ est partagée en trois parts proportionnelles aux nombres $3\;,\ 5\text{ et }7.$
Déterminer ces trois parts.
Exercice 9
Un magicien demande à un spectateur de :
penser à un nombre;
de le multiplier par deux;
de retrancher $3$ à ce produit;
de multiplier le tout par $6.$
Le spectateur annonce comme résultat $294.$
Quel était le nombre du départ ?
Exercice 10
Lorsqu'on descend un escalier comptant moins de $200$ marches, $2$ marches par $2$ marches, il en reste une.
Lorsqu'on le descend, $3$ marches par $3$ marches, il en reste $2.$
Lorsqu'on le descend, $4$ marches par $4$ marches, il en reste $3.$
Lorsqu'on le descend, $5$ marches par $5$ marches, il en reste $4.$
Lorsqu'on le descend, $6$ marches par $6$ marches, il en reste $5.$
Lorsqu'on le descend, $7$ marches par $7$ marches, il n'en reste pas.
Combien l'escalier a-t-il de marches ? Justifier votre réponse.
Application géométrique
1) Résoudre $x^{2}-6x+9=0$
2) Un géomètre prétend qu'on peut construire un triangle et un trapèze de même aire avec les dimensions suivantes (en cm).
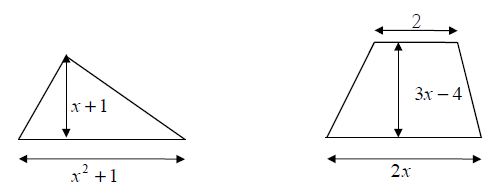
Si le géomètre a raison, pour quelle(s) valeur(s) de $x$ est-ce possible ?
Mise en équations
Exercice 1
Richard possède une certaine somme d'argent. Il envisage d'en dépenser les $2/3$ pour acheter un album de timbres, et d'en encaisser le quart en revendant ses timbres en double. Il lui restera alors $210\ frs$
Combien possède-t-il ?
Exercie 2
Un transporteur a livré $144$ caisses, toutes identiques, et $25$ fûts tous de même masse, en trois voyages. Le premier chargement de $56$ caisses et de $4$ fûts atteignait $3480\ kg.$ Le second de $40$ caisses et $7$ fûts pesait $4350\ kg.$
Quelle était la masse du dernier chargement ?
Exercice 3
Un âne porte $15$ sacs de sel et $2\ kg$ d'olives. Un mulet porte $2$ sacs de sel et $41\ kg$ d'olives. L'âne souffle fort! "De quoi te plains-tu ?" dit le mulet, "nous portons la même charge"
Quelle est la masse, en kilogramme, d'un sac de sel ?
Exercice 4
Une ficelle de $81\ cm$ est fixée à deux clous $A$ et $B$ distants de $45\ cm.$ On tend la ficelle jusqu'à un point $C$ tel que $ABC$ est un triangle rectangle en $A.$
Calculer alors les longueurs $AC$ et $BC.$
Exercice 5
La moyenne de six notes est $4.$ On ajoute une note et la moyenne devient $5.$
Quelle est cette septième note ?
Exercice 6
Peut-on trouver trois nombres entiers naturels consécutifs dont la somme vaut 1993 ?
Exercice 7
Dans ce demi-triangle équilatéral, déterminer $x$ pour que la hauteur $AH$ mesure $7\ cm.$

Exercice 8
David et Fabrice ont respectivement $15$ ans et $5$ ans.
Dans combien d'années l'âge de David sera-t-il le double de celui de Fabrice ?
Dans combien d'années sera-t-il le triple ?
Dans combien d'années sera-t-il le $6$ fois plus grand ?
Exercice 9
Un père a $27$ ans de plus que son fils. Dans $6$ ans, son âge sera le double de celui de son fils.
Quelles sont les âges du père et du fils ?
Exercice 10
Une mère de $37$ ans a trois enfants âgés de $8\;,\ 10\text{ et }13$ ans. Dans combien d'années l'âge de la mère sera-t-il égal à la somme des âges de ses enfants ?
Exercice 11
Pierre dit à Yves : "J'ai $5$ fois l'âge que tu avais quand j'avais l'âge que tu as". Yves lui répond : "Quand tu auras l'âge que j'ai, la somme de nos âges sera $84$ ans"
Quelle est l'âge de Pierre ?
Exercice 12
Quand le père avait l'âge du fils, le fils avait $10$ ans. Quand le fils aura l'âge du père, le père aura $70$ ans.
Quels sont leurs âges respectifs ?
Exercice 13
Si on augmente de $3$ mètres la longueur du côté d'un carré, l'aire augmente de $45\,m^{2}.$
Quelle est l'aire de ce carré ?

Commentaires
Anonyme (non vérifié)
jeu, 04/29/2021 - 08:16
Permalien
Correction svp
Ajouter un commentaire