Corrigé Bac Maths S1 2e groupe 2016

1. $C_{5}^{3}=10\;,\ C_{6}^{2}=15$ et $C_{10}^{4}=210$.

La proposition est fausse, car par exemple $C_{6}^{2}=15$ n'est pa un multiple de 6.

 

2. De la relation $C_{n}^{p}=\dfrac{n}{p}C_{n-1}^{p-1}$ on tire : $pC_{n}^{p}=nC_{n-1}^{p-1}$.

On y voit que $n$ divise $pC_{n}^{p}$; donc s'il est premier avec $p$, il doit d'après Gauss, diviser $C_{n}^{p}.$

$C_{n}^{p}$ est donc multiple de $n$.

La réciproque est fausse, car par exemple, $C_{10}^{4}=210$ est un multiple de 10 et pourtant 10 et 4 ne sont pas premiers entre eux.

 

3. $n$ étant premier, est premier avec tout entier $p$ compris entre 1 et $n-1$, par conséquent,

$C_{n}^{p}$ est un multiple de $n$ d'après la question précédente.

Pour tout couple d'entiers $(a,\ b)$ la formule du binôme entraîne $(a+b)^{n}-(a^{n}+b^{n})=\sum_{p=1}^{n-1}C_{n}^{p}a^{n-p}b^{p}$

 

c'est donc un multiple de $n$ puisque somme de multiples de $n.$

1. a. Si $x$ différent de $k\dfrac{\pi}{2}$ pour tout $k\in\mathbb{Z}$, alors $\tan x$ et $\tan 2x$ existent et sont non nuls.

 

$\dfrac{1}{\tan x}-\dfrac{2}{\tan 2x}=\dfrac{\cos x}{\sin x}-\dfrac{2\cos 2x}{\sin 2x}=\dfrac{\cos x}{\sin x}-\dfrac{\cos^{2}x-\sin^{2}x}{\sin x\cos s}=\dfrac{\sin x}{\cos x}=\tan x$

 

b. $f_{n}(x)=\sum_{p=0}^{n}\dfrac{1}{2^{p}}\tan\dfrac{x}{2^{p}}$

 

\begin{eqnarray}f_{n}(x) & = &\sum_{p=0}^{n}\dfrac{1}{2^{p}}\tan\dfrac{x}{2^{p}} \nonumber \\ & = & \sum_{p=0}^{n}\dfrac{1}{2^{p}}\left(\dfrac{1}{\tan \theta}-\dfrac{2}{\tan 2\theta}\right) \text{ d'après la question précédente, avec }\theta=\dfrac{x}{2^{p}} \nonumber \\& = & \sum_{p=0}^{n}\dfrac{1}{2^{p}\tan(x/2^{p})}-\dfrac{1}{2^{p-1}\tan(x/2^{p-1}} \nonumber \\& = & \sum_{p=0}^{n}\alpha_{p+1}-\alpha_{p}\quad\text{ avec }\alpha(p)=\dfrac{1}{2^{p-1}\tan(x/2^{p-1}} \nonumber \\& = & \alpha_{n+1}-\alpha_{0} \nonumber \\ f_{n}(x) & = & \dfrac{1}{2^{n}\tan(x/2^{n})}-\dfrac{2}{\tan 2x} \nonumber\end{eqnarray}

 

Mais aussi $f_{n}(x)=\dfrac{1}{2^{n}}\dfrac{\cos(x/2^{n})}{\sin(x/2^{n})}-2\dfrac{\cos 2x}{\sin 2x}$

 

2. 

\begin{eqnarray}I_{n} & = &\int_{\frac{\pi}{6}}^{\frac{\pi}{3}}f_{n}(t)\mathrm{d}t=\int_{\frac{\pi}{6}}^{\frac{\pi}{3}}\left(\dfrac{1}{2^{n}}\dfrac{\cos(t/2^{n})}{\sin(t/2^{n})}-2\dfrac{\cos 2t}{\sin 2t}\right)\mathrm{d}t \nonumber \\& = & \int_{\frac{\pi}{6}}^{\frac{\pi}{3}}\left(\dfrac{u'}{u}-\dfrac{v'}{v}\right)\mathrm{d}t\quad\text{ avec }u=\sin(t/2^{n})\text{ et }v=\sin 2t \nonumber \\& = & \left\lbrack\ln|u|-\ln|v|\right\rbrack_{t_{0}}^{2t_{0}}\quad\text{ avec }t_{0}=\frac{\pi}{6} \nonumber \\& = & \ln\sin(2t_{0}/2^{n})-\ln\sin(t_{0}/2^{n})-\ln\sin(4t_{0})+\ln\sin(2t_{0}) \nonumber \\& = & \ln\left(2\cos(t_{0}/2^{n})\right)+0 \nonumber \\I_{n} & = & \ln\left(2\cos\dfrac{\pi}{6\times 2^{n}}\right)  \nonumber\end{eqnarray}

 

3. Quand $n$ tend vers vers $+\infty\;,\ \dfrac{\pi}{6\times 2^{n}}$ tend vers 0 donc son cosinus tend vers 1 et $\lim_{n\rightarrow +\infty}I_{n}=\ln 2.$

Dans le repère donné, la conique $C$ a pour équation : $9x^{2}-4y^{2}-18x-8y-31=0.$

1. Pour tout point $M$ de coordonnées $(x,\ y)$ du plan,

$M\in C\Leftrightarrow 9(x-1)^{2}-4(y+1)^{2}=36\Leftrightarrow \dfrac{(x-1)^{2}}{4}-\dfrac{(y+1)^{2}}{9}=1$ 

 

$C$ est donc une hyperbole de centre le point 

$\Omega$ de coordonnées $(1,\ 1).$

2. $C$ a pour équation $\dfrac{(x-1)^{2}}{a^{2}}-\dfrac{(y+1)^{2}}{b^{2}}=1\text{ avce }a=2\text{ et }b=3$

 

Dans le repère $R'=(\Omega;\ \vec{i},\ \vec{j})$, $\ C$ a pour équation $\dfrac{x^{2}}{a^{2}}-\dfrac{y^{2}}{b^{2}}=1.$

Dans $R'$, ses sommets $S_{1}$ et $S_{2}$ ont pour coordonnée $(-a,\ 0)$ et $(a,\ 0)$ ; ses foyers $F_{1}$ et $F_{2}$ ont

pour coordonnées respectives $(c,\ 0)$ et $(-c,\ 0)$ avec $c=\sqrt{a^{2}+b^{2}}=\sqrt{13}$, son excentricité est $e=\dfrac{c}{a}=\dfrac{\sqrt{13}}{2}.$

Ses axes sont la droite passant par $\Omega$

 et de vecteur directeur $\vec{i}$ (axe focal) et la droite passant par $\Omega$ et de vecteur directeur $\vec{j}.$

Ses directrices ont pour équations respectives dans $R'$ : $x=-\dfrac{a^{2}}{c}=-\dfrac{4\sqrt{13}}{13}\text{ et }x=\dfrac{a^{2}}{c}=\dfrac{4\sqrt{13}}{13}.$

Ses asymptotes ont pour équations respectives dans $R'$ : $y=-\dfrac{b}{a}x=-\dfrac{3}{2}x\text{ et }y=\dfrac{b}{a}x=\dfrac{3}{2}x.$

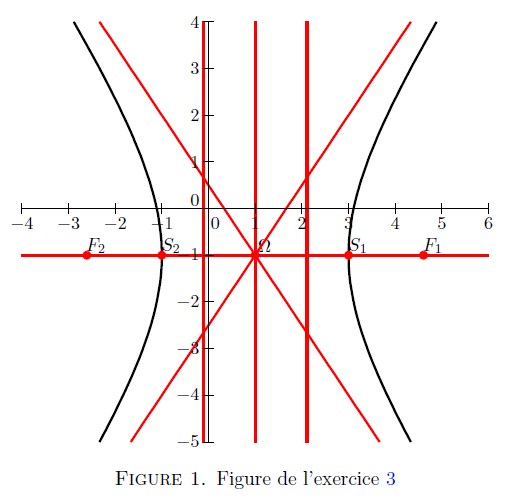
3. Tracer de $C$ voir figure 1.

1. Puisque $\Delta$ est la médiatrice de $[OO']$, $S_{\Delta}(O')=O$; donc $f\circ S_{\Delta}(O')=f(O)=O'.$

Puisque $f$ conserve les distance $AO=AO'$, donc $A$ appartient à $\Delta$ c'est à dire $S_{\Delta}(A)=A$;

alors $f\circ S_{\Delta}(A)=f(A)=A.$

2. Si $f\circ S_{\Delta}$ était l'application identique du plan, on en déduirait que $f=S_{\Delta}^{-1}=S_{\Delta}$; tous

les points de $\Delta$ seraient invariants par $f$, ce qui est impossible puisque $A$ est l'unique point invariant de $f.$

3. a. $f\circ S_{\Delta}$ est une isométrie distincte de l'application identique du plan et qui conserve les deux points $A$ et $O'$ ; c'est donc la réflexion d'axe $\Delta'=(AO')$

b. De $f\circ S_{\Delta}=S_{\Delta'}$ on déduit $f=S_{\Delta'}\circ S_{\Delta}^{-1}=S_{\Delta'}\circ S_{\Delta}.$

$f$, composée de deux réflexions dont les axes sont sécants en $A$, est une rotation de centre $A.$