Produit scalaire et lignes de niveau - 1er S

Soient $A_{1}\;,\ A_{2}\;,\ A_{3}\;,\ \ldots\;,\ A_{n}\;;\ n$ points du plan $\mathcal{P}$ affectés respectivement des réels $\alpha_{1}\;,\ \alpha_{2}\;,\ \alpha_{3}\;,\ \ldots\;,\ \alpha_{n}.$

 

On dit que $G$ est barycentre du système $(A_{i}, \alpha_{i})_{1\leq i\leq n}$ si, et seulement si,

$$\alpha_{1}\overrightarrow{GA}_{1}+\alpha_{2}\overrightarrow{GA}_{2}+\alpha_{3}\overrightarrow{GA}_{3}+\ldots+\alpha_{n}\overrightarrow{GA}_{n}=\vec{0}\quad\text{ avec }\;\alpha_{1}+\alpha_{2}+\alpha_{3}+\ldots+\alpha_{n} \neq 0$$

 

On a :

$$\sum_{i=1}^{n} \alpha_{i}\overrightarrow{GA}_{i}=\vec{0}\quad\text{ avec }\;\sum_{i=1}^{n} \alpha_{i} \neq 0$$

$\centerdot\ \ $ Si $\alpha_{1}=\alpha_{2}=\alpha_{3}=\ldots=\alpha_{n}$ (tous les coefficients égaux) on dira que $G$ est isobarycentre de $A_{1}\;,\ A_{2}\;,\ A_{3}\;,\ \ldots\;,\ A_{n}$

 

$-\ $ l'isobarycentre de deux points  $A_{1}$ et $A_{2}$ est le milieu de  $[A_{1}A_{2}]$

 

$-\ $ l'isobarycentre de trois points non alignés $A_{1}\;,\ A_{2}$ et $A_{3}$ est le centre de gravité du triangle $A_{1}A_{2}A_{3}$ (le point de rencontre des médianes) 
 

 

 

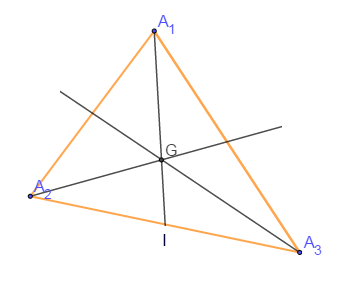
$\overrightarrow{A_{1}G}=\dfrac{2}{3}\overrightarrow{A_{1}I}\;,\quad\overrightarrow{A_{1}G}=2\overrightarrow{GI}\;,\quad\overrightarrow{IG}=\dfrac{1}{3}\overrightarrow{IA_{1}}$

Soient $(A_{1}\;;\ \alpha_{1})\;,\ (A_{2}\;;\ \alpha_{2})\;,\ \ldots\;,\ (A_{n}\;;\ \alpha_{n})\;,\ n$ points pondérés.

 

$G$ barycentre de $(A_{1}\;;\ \alpha_{1})\;,\ (A_{2}\;;\ \alpha_{2})\;,\ \ldots\;,\ (A_{n}\;;\ \alpha_{n})$ si, et seulement si,

$$\forall\;M\in\mathcal{P}\;,\ \alpha_{1}\overrightarrow{MA}_{1}+\alpha_{2}\overrightarrow{MA}_{2}+\ldots+\alpha_{n}\overrightarrow{MA}_{n}=(\alpha_{1}+\alpha_{2}+\ldots+\alpha_{n})\overrightarrow{MG}$$

avec $\;\alpha_{1}+\alpha_{2}+\ldots+\alpha_{n}\neq 0$

Soit $G$ barycentre de $(A_{1}\;;\ \alpha_{1})\;,\ (A_{2}\;;\ \alpha_{2})\;,\ \ldots\;,\ (A_{n}\;;\ \alpha_{n}).$

 

Si $G_{1}$ est barycentre de $(A_{1}\;;\ \alpha_{1})\;,\ (A_{3}\;;\ \alpha_{3})\;,\ (A_{5}\;;\ \alpha_{5})$ alors $G$ barycentre de $$(G_{1}\;;\ \alpha_{1}+\alpha_{3}+\alpha_{5})\;,\ (A_{2}\;;\ \alpha_{2})\;,\ (A_{4}\;;\ \alpha_{4})\;,\ (A_{6}\;;\ \alpha_{6})\;,\ \ldots\;,\ (A_{n}\;;\ \alpha_{n})$$

Si $G$ barycentre de $(A_{1}\;;\ \alpha_{1})\;,\ (A_{2}\;;\ \alpha_{2})\;,\ \ldots\;,\ (A_{n}\;;\ \alpha_{n})$ alors 

$$\forall\;M\in\mathcal{P}\;,\ \overrightarrow{MG}=\dfrac{\alpha_{1}\overrightarrow{MA}_{1}+\alpha_{2}\overrightarrow{MA}_{2}+\ldots+\alpha_{n}\overrightarrow{MA}_{n}}{\alpha_{1}+\alpha_{2}+\ldots+\alpha_{n}}$$

 

Dans le plan muni du repère $(O\;;\ \vec{i}\;,\ \vec{j})$, pour $M=O$ on a :

$$\overrightarrow{OG}=\dfrac{\alpha_{1}\overrightarrow{OA}_{1}+\alpha_{2}\overrightarrow{OA}_{2}+\ldots+\alpha_{n}\overrightarrow{OA}_{n}}{\alpha_{1}+\alpha_{2}+\ldots+\alpha_{n}}$$

 

Donc, $G$ a pour coordonnées :

 

$$x_{G}=\dfrac{\alpha_{1}.x_{A_{1}}+\alpha_{2}.x_{A_{2}}+\alpha_{3}.x_{A_{3}}+\ldots+\alpha_{n}.x_{A_{n}}}{\alpha_{1}+\alpha_{2}+\ldots+\alpha_{n}}$$

$$y_{G}=\dfrac{\alpha_{1}.y_{A_{1}}+\alpha_{2}.y_{A_{2}}+\alpha_{3}.y_{A_{3}}+\ldots+\alpha_{n}.y_{A_{n}}}{\alpha_{1}+\alpha_{2}+\ldots+\alpha_{n}}$$

Pour construire le point $G$ on peut choisir $M$ égal à un des $A_{i}.$

Pour $M=A_{1}$ on aura 

 

$$\overrightarrow{A_{1}G}=\dfrac{\alpha_{2}\overrightarrow{A_{1}A}_{2}+\alpha_{3}\overrightarrow{A_{1}A}_{3}+\ldots+\alpha_{n}\overrightarrow{A_{1}A}_{n}}{\alpha_{1}+\alpha_{2}+\ldots+\alpha_{n}}$$

 

En particulier, si $G$ barycentre du système $(A\;,\ \alpha)\;,\ (B\;,\ \beta)\;,\ (C\;,\ \gamma)$ on a, d'après la propriété caractéristique $$\overrightarrow{MG}=\dfrac{\alpha\overrightarrow{MA}+\beta\overrightarrow{MB}+\gamma\overrightarrow{MC}}{\alpha+\beta+\gamma}$$

Donc, pour construire $G$ on choisira $M=A$ ou $M=B$ ou encore $M=C.$

 

Soit $M=A$ , on a :

$$\overrightarrow{AG}=\dfrac{\beta\overrightarrow{AB}+\gamma\overrightarrow{AC}}{\alpha+\beta+\gamma}=\dfrac{\beta\overrightarrow{AB}}{\alpha+\beta+\gamma}+\dfrac{\gamma\overrightarrow{AC}}{\alpha+\beta+\gamma}$$

Donc dans le repère $(A\;;\  \overrightarrow{AB}\;,\  \overrightarrow{AC})\;,\ G$ aura pour coordonnées :

$$x_{G}=\dfrac{\beta}{\alpha+\beta+\gamma}$$

$$y_{G}=\dfrac{\gamma}{\alpha+\beta+\gamma}$$

$A\;,\ B\;,\ C$ et $D$ sont quatre points du plan tels que trois quelconques d'entre eux ne sont pas alignés.

 

$G$ barycentre du système $(A\;,\ 1)\;,\ (B\;,\ 2)\;,\ (C\;,\ 2)\;,\ (D\;,\ 1)$

 

1) Placer le point $I$ barycentre de $(A\;,\ 1)\;,\ (B\;,\ 2)$

 

2) Placer le point $J$ barycentre de $(C\;,\ 2)\;,\ (D\;,\ 1)$

 

3) Démontrer que $G\in(IJ)$

 

4) On désigne par $K$ le milieu de $[AD]$ et $L$ le milieu de $[BC].$ Démontrer que les points $G\;,\ K$ et $L$ sont alignés.

1) $I$ barycentre de $(A\;,\ 1)\;,\ (B\;,\ 2)$ alors $\overrightarrow{AI}=\dfrac{2}{1+2}\overrightarrow{AB}\;\Rightarrow\;\overrightarrow{AI}=\dfrac{2}{3}\overrightarrow{AB}$

 

2) $J$ barycentre de $(C\;,\ 2)\;,\ (D\;,\ 1)$ alors $\overrightarrow{CJ}=\dfrac{1}{2+1}\overrightarrow{CD}\;\Rightarrow\;\overrightarrow{CJ}=\dfrac{1}{3}\overrightarrow{CD}$
 

 

 

3) On a $G$ barycentre du système $(A\;,\ 1)\;,\ (B\;,\ 2)\;,\ (C\;,\ 2)\;,\ (D\;,\ 1)$ et comme $I$ est barycentre de $(A\;,\ 1)\;,\ (B\;,\ 2)$ et $J$ barycentre de $(C\;,\ 2)\;,\ (D\;,\ 1)$ alors, $G$ sera barycentre du système $(I\;,\ 3)\;,\ (J\;,\ 3)$

 

Donc, $3\overrightarrow{GI}+3\overrightarrow{GJ}=\vec{0}\;\Rightarrow\;\overrightarrow{IG}=\dfrac{1}{2}\overrightarrow{IJ}$

 

Ainsi, $G\in(IJ)$

 

4) $K$ milieu de $[AD]$ alors  $K$ est barycentre de $(A\;,\ 1)\;,\ (D\;,\ 1)$

 

$L$ milieu de $[BC]$ alors $L$ est barycentre de $(B\;,\ 2)\;,\ (C\;,\ 2)$

 

et donc, $G$ est barycentre de $(K\;,\ 2)\;,\ (L\;,\ 4)$

 

Par conséquent, $G\;,\ K$ et $L$ sont alignés.

$\centerdot\ \ $ Soient $\vec{u}$ et $\vec{v}$ deux vecteurs non nuls. Il existe trois points $A\;,\ B$ et $C$ tels que $\overrightarrow{AB}=\vec{u}$ et $\overrightarrow{AC}=\vec{v}.$

 

On appelle produit scalaire de $\vec{u}$ et $\vec{v}$ le réel noté $$\vec{u}\cdot\vec{v}=\overrightarrow{AB}\cdot\overrightarrow{AC}=\overline{AB}\times\overline{AH}=\overline{AH'}\times\overline{AC}$$ où $H$ est le projeté orthogonal de $C$ sur $(AB)$ et $H'$ le projeté orthogonal de $B$ sur $(AC).$

 

$\centerdot\ \ $ On a $$\vec{u}\cdot\vec{v}=\overrightarrow{AB}\cdot\overrightarrow{AC}=||\overrightarrow{AB}||\times||\overrightarrow{AC}||\times\cos(\overrightarrow{AB},\ \overrightarrow{AC})$$

 

$\centerdot\ \ $  Dans un repère orthonormé direct $(O\;;\ \vec{i}\;,\ \vec{j})$ si $\vec{u}\begin{pmatrix} x\\ y\end{pmatrix}$ et $\vec{v}\begin{pmatrix} x'\\ y'\end{pmatrix}$ sont deux vecteurs dans cette base, alors on a $$\vec{u}\cdot\vec{v}=xx'+yy'$$

Soient $\vec{u}\;,\ \vec{v}\;,\ \vec{w}$ trois vecteurs , $\;\alpha\;,\ \beta\in\mathbb{R}.$

 

On a :

 

$\centerdot\ \ \vec{u}\cdot\vec{v}=\vec{v}\cdot\vec{u}$

 

$\centerdot\ \ (\alpha\vec{u})\cdot(\beta\vec{v})=\alpha.\beta(\vec{u}\cdot\vec{v})$

 

$\centerdot\ \ \vec{u}\cdot(\vec{v}+\vec{w})=\vec{u}\cdot\vec{v}+\vec{u}\cdot\vec{w}$

 

$\centerdot\ \ \vec{u}\neq\vec{0}\;,\  \vec{v}\neq\vec{0}\;\text{ alors }\; \vec{u}\cdot\vec{v}=0\;\Leftrightarrow\;\vec{u}\perp\vec{v}$

 

$\centerdot\ \ (\vec{u}+\vec{v})^{2}=\vec{u}^{2}+\vec{v}^{2}+2\vec{u}\cdot\vec{v}$

 

$\centerdot\ \ (\vec{u}-\vec{v})^{2}=\vec{u}^{2}+\vec{v}^{2}-2\vec{u}\cdot\vec{v}$

 

$\centerdot\ \ (\vec{u}+\vec{v})\cdot(\vec{u}-\vec{v})=\vec{u}^{2}-\vec{v}^{2}$

 

a) Soit $\vec{u}$ un vecteur donné ; $\mathbf{E}_{k}=\left\lbrace M\in\mathcal{P}\;;\  \vec{u}\cdot\overrightarrow{AM}=k\right\rbrace$ est la perpendiculaire à la direction de $\vec{u}.$ 

 

b) $\mathbf{E}=\left\lbrace M\in\mathcal{P}\;;\ MA=MB\right\rbrace$ est la médiatrice du segment $[AB].$

 

En effet, soit $I$ milieu de $[AB]$ , on a :

 

$\begin{array}{rcl} MA=MB&\Leftrightarrow&MA^{2}=MB^{2}\\ \\&\Leftrightarrow&MA^{2}-MB^{2}=0\\ \\&\Leftrightarrow&(\overrightarrow{MA}-\overrightarrow{MB})\cdot(\overrightarrow{MA}+\overrightarrow{MB})=0\\ \\&\Leftrightarrow&(\overrightarrow{MI}+\overrightarrow{IA}-\overrightarrow{MI}-\overrightarrow{IB}) \cdot(\overrightarrow{MI}+\overrightarrow{IA}+\overrightarrow{MI}+\overrightarrow{IB})=0\\ \\&\Leftrightarrow&2\overrightarrow{BA}\cdot \overrightarrow{MI}=0\\ \\&\Leftrightarrow&\overrightarrow{AB}\cdot \overrightarrow{MI}=0\end{array}$

 

On reconnait la perpendiculaire à $(AB)$ passant par $I$ encore appelée médiatrice du segment $[AB].$

 

c) $\mathbf{E}_{k}=\left\lbrace M\in\mathcal{P}\;;\  MA=k\in\mathbb{R}_{+}^{*}\right\rbrace$ est le cercle de centre $A$ et de rayon $k.$

$$\mathbf{E}_{k}=\mathcal{C}(A\;,\ k)$$

d) Soit $\mathbf{E}_{k}=\left\lbrace M\in\mathcal{P}\;;\  \overrightarrow{MA}\cdot\overrightarrow{MB}=k\right\rbrace$ et $I$ milieu de $[AB].$

 

On a :

 

$\begin{array}{rcl}\overrightarrow{MA}\cdot\overrightarrow{MB}&=&(\overrightarrow{MI}+\overrightarrow{IA})\cdot(\overrightarrow{MI}+\overrightarrow{IB})\\ \\&=&MI^{2}+\overrightarrow{MI}\cdot\underbrace{(\overrightarrow{IA}+\overrightarrow{IB})}_{=\vec{0}}+\overrightarrow{IA}\cdot\overrightarrow{IB}\\ \\ \Rightarrow\; \overrightarrow{MA}\cdot\overrightarrow{MB}&=&MI^{2}-\dfrac{\overrightarrow{AB}}{2}\cdot\dfrac{\overrightarrow{AB}}{2}\quad\text{or }\;\overrightarrow{MA}\cdot\overrightarrow{MB}=k\\ \\ \Rightarrow\;\ \qquad MI^{2}&=&k+\dfrac{AB^{2}}{4}\end{array}$

 

$-\ $ si $k+\dfrac{AB^{2}}{4}<0\;,\  \mathbf{E}_{k}=\emptyset$

 

$-\ $ si $k+\dfrac{AB^{2}}{4}=0\;,\  \mathbf{E}_{k}=\{I\}$

 

$-\ $ si $k+\dfrac{AB^{2}}{4}>0$ alors $MI=\sqrt{k+\dfrac{AB^{2}}{4}}$

 

Donc, $\mathbf{E}_{k}$ est le cercle de centre $I$ et de rayon $r=\sqrt{k+\dfrac{AB^{2}}{4}}$

 

$$\mathbf{E}_{k}=\mathcal{C}\left(I\;,\ \sqrt{k+\dfrac{AB^{2}}{4}}\right)$$

Si $k=0$ on a $\overrightarrow{MA}\cdot\overrightarrow{MB}=0$

 

Donc, ${E}_{k}$ est le cercle de diamètre $[AB].$

Déterminer l'ensemble des points $M$ du plan tels que :

$$||\overrightarrow{MA}+\overrightarrow{MB}||=||\overrightarrow{MA}-2\overrightarrow{MB}+4\overrightarrow{MC}||$$

Soit $G$ barycentre de $(A\;;\ 1)\;,\ (B\;;\ 1)$ et $I$ barycentre de $(A\;;\ 1)\;,\ (B\;;\ -2)\;,\ (C\;;\ 4)$

 

On a :

 

$\begin{array}{rcl}||\overrightarrow{MA}+\overrightarrow{MB}||=||\overrightarrow{MA}-2\overrightarrow{MB}+4\overrightarrow{MC}||&\Leftrightarrow&||2\overrightarrow{MG}||=||3\overrightarrow{MI}||\\ \\&\Leftrightarrow&4MG^{2}-9MI^{2}=0\\ \\ &\Leftrightarrow &(2\overrightarrow{MG}-3\overrightarrow{MI})\cdot(2\overrightarrow{MG}+3\overrightarrow{MI})=0\end{array}$

 

Considérons $H$ barycentre de $(G\;;\ 2)\;,\ (I\;;\ -3)$ et $D$ barycentre de $(G\;;\ 2)\;,\ (I\;;\ 3)$

 

Alors on a :

 

$\begin{array}{rcrcl} -\overrightarrow{MH}\cdot 5\overrightarrow{MD}=0&\Leftrightarrow& -5\overrightarrow{MH}\cdot\overrightarrow{MD}&=&0\\ \\&\Leftrightarrow&\overrightarrow{MH}\cdot\overrightarrow{MD}&=&0\end{array}$ 

 

et donc l'ensemble des points $M$ du plan tels que $||\overrightarrow{MA}+\overrightarrow{MB}||=||\overrightarrow{MA}-2\overrightarrow{MB}+4\overrightarrow{MC}||$ est le cercle de diamètre $[HD].$

 

e) $\mathbf{E}_{k}=\left\lbrace M\in\mathcal{P}\;;\  \alpha MA^{2}+\beta MB^{2}+\gamma MC^{2}=k\right\rbrace$

 

$\centerdot\ \ 1^{e}$ cas : $\;\alpha+\beta+\gamma\neq 0$

 

Soit $G$ barycentre de $(A\;,\ \alpha)\;,\ (B\;,\ \beta)$ et $(C\;,\ \gamma).$

 

On a :

 

$\begin{array}{ll}&\alpha MA^{2}+\beta MB^{2}+\gamma MC^{2}=k\\ \\ \Leftrightarrow&\alpha(\overrightarrow{MG}+\overrightarrow{GA})^{2}+\beta(\overrightarrow{MG}+\overrightarrow{GB})^{2}+\gamma(\overrightarrow{MG}+\overrightarrow{GC})^{2}=k\\ \\ \Leftrightarrow& \alpha(MG^{2}+2\overrightarrow{MG}\cdot\overrightarrow{GA}+GA^{2})+\beta(MG^{2}+2\overrightarrow{MG}\cdot\overrightarrow{GB}+GB^{2})+\gamma(MG^{2}+2\overrightarrow{MG}\cdot \overrightarrow{GC}+GC^{2})=k\\ \\ \Leftrightarrow& (\alpha+\beta+\gamma)MG^{2}+2\alpha\overrightarrow{MG}\cdot\overrightarrow{GA}+2\beta\overrightarrow{MG}\cdot\overrightarrow{GB}+2\gamma\overrightarrow{MG}\cdot\overrightarrow{GC}+\alpha GA^{2}+\beta GB^{2}+\gamma GC^{2}=k\\ \\ \Leftrightarrow& (\alpha+\beta+\gamma)MG^{2}+2\overrightarrow{MG}\cdot\underbrace{(\alpha\overrightarrow{GA}+\beta\overrightarrow{GB}+\gamma\overrightarrow{GC})}_{=\vec{0}}+\alpha GA^{2}+\beta GB^{2}+\gamma GC^{2}=k\end{array}$

 

Ce qui donne : $MG^{2}=\dfrac{k-\alpha GA^{2}-\beta GB^{2}-\gamma GC^{2}}{\alpha+\beta+\gamma}$

 

$-$ si $\;\dfrac{k-\alpha GA^{2}-\beta GB^{2}-\gamma GC^{2}}{\alpha+\beta+\gamma}<0\;,\  \mathbf{E}_{k}=\emptyset$

 

$-$ si $\;\dfrac{k-\alpha GA^{2}-\beta GB^{2}-\gamma GC^{2}}{\alpha+\beta+\gamma}=0\;,\  \mathbf{E}_{k}=\{G\}$

 

$-$ si $\;\dfrac{k-\alpha GA^{2}-\beta GB^{2}-\gamma GC^{2}}{\alpha+\beta+\gamma}>0\;$ alors $\;MG=\sqrt{\dfrac{k-\alpha GA^{2}-\beta GB^{2}-\gamma GC^{2}}{\alpha+\beta+\gamma}}$

 

Donc, $\mathbf{E}_{k}$ est le cercle de centre $G$ et de rayon $r=\sqrt{\dfrac{k-\alpha GA^{2}-\beta GB^{2}-\gamma GC^{2}}{\alpha+\beta+\gamma}}$

 

$$\mathbf{E}_{k}=\mathcal{C}\left(G\;,\ \sqrt{\dfrac{k-\alpha GA^{2}-\beta GB^{2}-\gamma GC^{2}}{\alpha+\beta+\gamma}}\right)$$

 

$\centerdot\ \ 2^{e}$ cas : $\;\alpha+\beta+\gamma=0$

 

On a :

 

$\begin{array}{ll}&\alpha MA^{2}+\beta MB^{2}+\gamma MC^{2}=k\\ \\ \Leftrightarrow&\alpha\overrightarrow{MA}^{2}+\beta(\overrightarrow{MA}+\overrightarrow{AB})^{2}+\gamma(\overrightarrow{MA}+\overrightarrow{AC})^{2}=k\\ \\ \Leftrightarrow&\alpha MA^{2}+\beta(MA^{2}+2\overrightarrow{MA}\cdot\overrightarrow{AB}+AB^{2})+\gamma(MA^{2}+2\overrightarrow{MA}\cdot\overrightarrow{AC}+AC^{2})=k\\ \\ \Leftrightarrow&\underbrace{(\alpha+\beta+\gamma)}_{=0}MA^{2}+2\overrightarrow{MA}\cdot(\beta\overrightarrow{AB}+\gamma\overrightarrow{AC})+\beta AB^{2}+\gamma AC^{2}=k\\ \\ \Leftrightarrow&2\overrightarrow{MA}\cdot\underbrace {(\beta\overrightarrow{AB}+\gamma\overrightarrow{AC})}_{=\vec{u}}+\beta AB^{2}+\gamma AC^{2}=k\end{array}$

 

Ainsi, $2\overrightarrow{MA}\cdot\vec{u}=k-\beta AB^{2}-\gamma AC^{2}$

 

Par suite, $\overrightarrow{MA}\cdot\vec{u}=\dfrac{k-\beta AB^{2}-\gamma AC^{2}}{2}$

 

$\mathbf{E}_{k}$ est donc une droite orthogonale à la direction de $\vec{u}.$