Corrigé Bac Maths S2 2e groupe 2017

1) La relation $|z'|=1$ est équivalente à : $\left|\dfrac{\mathrm{i}z+\mathrm{i}+1}{z+2}\right|=1$, soit en factorisant par $\mathrm{i}$ au numérateur :

$$\begin{eqnarray}\left|\dfrac{\mathrm{i}\left( z+\frac{\mathrm{i}+1}{\mathrm{i}}\right)}{z+2}\right|=1 &\Leftrightarrow& \dfrac{|\mathrm{i}|\times|z+1-\mathrm{i}|}{|z+2|}=1 \nonumber \\ &\Leftrightarrow& |z+1-\mathrm{i}|=|z+2|\quad(\text{car }|\mathrm{i}|=1) \nonumber \end{eqnarray}$$

 

Cette dernière relation s'écrit, d'après les données de l'énoncé:

 

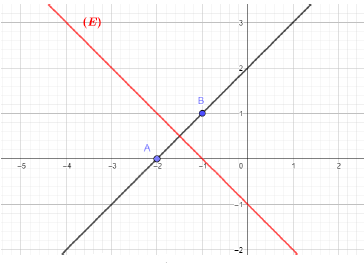
$|z-z_{B}|=|z-z_{A}|$ et s'interprète géométriquement par $MA=MB.$

 

L'ensemble $E$ n'est donc autre que la médiatrice du segment $[AB].$

2) a) Une première application de la méthode de Hörner donne :

 

$$\begin{array}{|c|c|c|c|c|}\hline &1&-2+\mathrm{i}&1&-2+\mathrm{i} \\ \hline\mathrm{i}& &\mathrm{i}  &-2-2\mathrm{i}&2-\mathrm{i} \\ \hline &1&-2+2\mathrm{i}&-1-2\mathrm{i}&0 \\ \hline\end{array}$$

 

Ceci montre que $P(\mathrm{i})=0$ et que $P(z)=(z-\mathrm{i})(z^{2}+(-2+2\mathrm{i})z-1-2\mathrm{i}).$

 

Soit $Q(z)$ le polynôme $z^{2}+(-2+2\mathrm{i})z-1-2\mathrm{i}.$ Appliquons à nouveau la méthode de Hörner à $Q(z).$

 

$$\begin{array}{|c|c|c|c|}\hline &1&-2+2\mathrm{i}&-1-2\mathrm{i} \\ \hline -\mathrm{i}& &-\mathrm{i} &1+2\mathrm{i} \\ \hline &1&-2+\mathrm{i}&0 \\ \hline\end{array}$$

 

On obtient alors : $Q(z)=(z+\mathrm{i})(z-2+\mathrm{i}).$ D'où $Q(-\mathrm{i}=0$

 

Il en résulte immédiatement que $\mathrm{i}$ et $-\mathrm{i}$ sont bien racines de $P(z).$

 

b) Finalement, on peut écrire : $P(z)=(z-\mathrm{i})(z+\mathrm{i})(z-2+\mathrm{i})$

 

Commentaire : Exercice classique et relativement simple sur les nombres complexes.

1) En donnant à $n$ les valeurs, 1, 2, 3 et 4 successivement dans l'expression de $U_{n}$, on obtient : $$U_{1}=\ln 3\;;\quad U_{2}=\ln\left(\dfrac{5}{3}\right)\;;\quad U_{3}=\left(\dfrac{7}{5}\right)\;;\quad U_{4}=\left(\dfrac{9}{7}\right)$$

 

2) D'après la propriété fondamentale du logarithme népérien : 

 

$U_{1}+U_{2}+U_{3}+U_{4}=\ln 3+\ln\left(\dfrac{5}{3}\right)+\ln\left(\dfrac{7}{5}\right)+\ln\left(\dfrac{9}{7}\right)=\ln\left(3\times\dfrac{5}{3}\times\dfrac{7}{5}\times\dfrac{9}{7}\right)$

 

Soit : $$U_{1}+U_{2}+U_{3}+U_{4}=\ln 9$$

 

3) D'après le théorème sur la limite d'une composée de suites, on a :

 

$\lim_{n\rightarrow +\infty}\dfrac{2n+1}{2n-1}=\lim_{n\rightarrow +\infty}\dfrac{2n}{2n}=1$, d'où $\lim_{n\rightarrow +\infty}\ln\dfrac{2n+1}{2n-1}=\ln 1=0$

 

La suite $(U_{n})$ converge vers 0.

 

4) a) Procédons par récurrence. Soit $(P_{n})$ la propriété :

$$"\text{Pour tout }n\geq 1\;,\ S_{n}=\ln(2n+1)"$$

Elle est vraie pour $n=1$ car $S_{1}=U_{1}=\ln 3$ et $\ln(2\times 1+1)=\ln 3.$

 

Supposons-la vraie pour l'entier $n$, c'est-à-dire que : 

$$S_{n}=U_{1}+U_{2}+\cdots+U_{n}=\ln(2n+1)$$

 

Alors 

$$\begin{eqnarray} S_{n+1} &=& (U_{1}+U_{2}+\cdots+U_{n})+U_{n+1} \nonumber \\ &=& \ln(2n+1)+\ln\dfrac{2(n+1)+1}{2(n+1)-1} \nonumber \\ &=& \ln(2n+1)+\ln\dfrac{2n+3}{2n+1} \nonumber \\ &=& \ln\left[(2n+1)\times\dfrac{2n+3}{2n+1}\right] \nonumber \\ &=& \ln(2n+3) \nonumber \end{eqnarray}$$

 

D'où la propriété est encore vraie pour $(n+1).$

 

On déduit alors du principe de récurrence qu'elle est vraie pour tout entier $n$ supérieur ou égal à 1.

 

5) D'après le théorème sur la limite d'une composée de suites, on a :

$\lim_{n\rightarrow +\infty}(2n+1)=+\infty$  et $\lim_{x\rightarrow +\infty}\ln x=+\infty$  ce qui entraîne que $\lim_{n\rightarrow +\infty}S_{n}=+\infty.$

 

Commentaire : L'exercice ne présente guère de difficulté. Il fallait rédiger soigneusement le raisonnement par récurrence. C'est la méthode la plus rigoureuse pour traiter des questions telles que le 4). La question 5) nous parait peu pertinente.

1) On a affaire à une équation différentielle linéaire du premier ordre. Les solutions, d'après le cours, sont les fonctions $y$ de la forme : $y=K\mathrm{e}^{2x}$, où $K$ est une constante réelle arbitraire.

 

2) a) $f$ est de la forme $K\mathrm{e}^{2x}$. La condition $f(0)=\dfrac{1}{2}$ entraîne que $K\mathrm{e}^{0}=\dfrac{1}{2}$, soit $K=\dfrac{1}{2}.$

 

D'où finalement : $f(x)=\dfrac{1}{2}\mathrm{e}^{2x}$

 

b) Une primitive sur $\mathbb{R}$ de la fonction $f$ est : $\mathrm{e}^{2x}.$ On a donc par définition de l'intégrale : $$\int_{0}^{a}f(x)\mathrm{d}x=\left[\mathrm{e}^{2x}\right]_{0}^{a}=\mathrm{e}^{2a}-1$$

 

Nous souhaitons que la valeur de cette intégrale soit 2, d'où 

$$\begin{eqnarray} \mathrm{e}^{2a}=3 &\Rightarrow& 2a=\ln 3 \nonumber \\ &\Rightarrow& a=\ln\sqrt{3} \nonumber \end{eqnarray}$$

1) On peut résoudre ce système par la méthode du pivot, mais il est plus simple de remarquer qu'en faisant la somme des deux premières équations, on a la relation : 

$$\begin{eqnarray} 2x+2z=22 &\Rightarrow& x+z=11 \nonumber \\ &\Rightarrow& x=11-z\quad(*) \nonumber \end{eqnarray}$$

 

Substituant cette expression de $x$ dans la troisième équation, on a : 

 

$11-z-4y+19z=153\ \Rightarrow\ y=\dfrac{9z-71}{2}\quad(**).$

 

Reportons alors ces expressions de $x$ et $y$ en fonction de $y$ dans la première équation pour obtenir :  $11-z+\dfrac{9z-71}{2}+z=16$, soit après simplification : $z=9.$

 

En remplaçant $z$ par cette valeur numérique dans (*) et (**), on trouve finalement que :

$y=5$ et $x=2.$

 

L'ensemble des solutions de ce système est, finalement : $$S=\{(2\;;\ 5\;;\ 9)\}$$

 

2) a) D'après les formules relatives aux caractéristiques d'une série statistique et les données du tableau de l'énoncé, on a :

 

$$\bar{X}=\dfrac{a+b+c+24}{6}\;;\quad\bar{Y}=\dfrac{a-b+c+8}{6}$$

 

et $$\dfrac{1}{6}\sum_{i=1}^{6}x_{i}y_{i}=\dfrac{-3a+4a+4b-8b+7c+12c}{6}=\dfrac{a-4b+19c}{6}$$

 

b) Les données $\bar{X}=\dfrac{40}{6}\;,\ \bar{Y}=\dfrac{14}{6}$ et $cov(X\;,\ Y)=\dfrac{179}{18}$ se traduisent, d'après les expressions obtenues au a) par :

 

$a+b+c+24=40\;;\quad a-b+c+8=14\;;\quad\dfrac{1}{6}\sum_{i=1}^{6}x_{i}y_{i}-\bar{X}\bar{Y}=\dfrac{179}{18}$

 

La dernière relation s'écrit encore : $\dfrac{a-4b+19c}{6}-\dfrac{40\times 14}{36}=\dfrac{179}{18}$ soit en réduisant au même dénominateur : 

$$\begin{eqnarray}\dfrac{6(a-4b+19c)-560}{36}=\dfrac{358}{36} &\Leftrightarrow& 6(a-4b+19c)=918 \nonumber \\ &\Leftrightarrow& a-4b+19c=\dfrac{918}{6}=153 \nonumber \end{eqnarray}$$

 

On a donc le système : $$\left\lbrace\begin{array}{rcl} a+b+c &=& 16\\ a-b+c &=& 6\\ a-4b+19c &=& 153 \end{array}\right.$$

qui est identique à celui de la première question en remplaçant $x\;,\ y$ et $z$ par $a\;,\ b$ et $c$ respectivement.

 

Il résulte de la résolution de la première question que $a=2\;,\ b=3$ et $c=9.$

Auteur: Mouhamadou Ka