Série d'exercices sur la statistique 1e S
Exercice 1
1) L'ensemble des habitants de Dakar.
2) L'ensemble des étudiants inscrits à l'université de Dakar en $2013.$
Réponses :
1) L'ensemble des habitants de Dakar n'est pas une population définie car :
l'année n'est pas précisée les individus qui sont immigrants à Dakar et qui y résident une partie seulement de l'année sont-ils réellement des habitants de Dakar ?
2) L'ensemble des étudiants de l'UCAD en $2013$ est bien défini et peut être utilisé sans ambiguïté pour une étude statistique car on connait de façon sure qui est ou n'est pas étudiant inscrit à l'UCAD en $2013.$
Exercice 2
le sexe, l'âge, la taille, le poids, la nationalité, la tension artérielle, la situation matrimoniale, le coefficient intellectuel.
Exercice 3
1) la taille des individus d'une population donnée
2) le coefficient intellectuel
3) la durée des appels d'un téléphone portable d'un individu durant une journée donnée
4) le nombre de candidats d'un jury de baccalauréat en $2013$, au Sénégal
5) les notes de mathématiques sur $20$, de l'ensemble des candidats au baccalauréat au Sénégal en $2013$
Exercice 4
$$\begin{array}{|c|c|c|c|c|c|} \hline \text{Modalités}&M_{1}&M_{2}&M_{3}&M_{4}&M_{5} \\ \hline \text{Fréquences }f_{i}&0.11&0.31&0.13&0.25&f_{5} \\ \hline \end{array}$$
Exercice 5
amplitudes ayant pour centres respectifs : $22\;,\ 32\;,\ 42\;,\ 52\;,\ 62\;,\text{ et }72.$
1) Quelle est l'amplitude $a$ de chaque classe ?
2) Déterminer chacune de ces $6$ classes
3) La moyenne de la série statistique correspondante peut-elle être égale à :
$20$ ? $84$ ? $36$ ?
4) La variance de cette série peut-elle être égale à :
$-18$ ? $0.32$ ?
Exercice 6
$$\begin{array}{|c|c|c|c|c|c|c|} \hline \text{Poids en }kg&30&40&60&80&90&100 \\ \hline \text{Effectifs}&10&20&10&30&40&n \\ \hline \end{array}$$
Déterminer l'effectif $n$ sachant que la moyenne de cette série est $83.5\;kg.$
Exercice 7
$$\begin{array}{|c|c|c|c|c|c|} \hline \text{Taille en }cm&[160\;,\ 170[&[170\;,\ 180[&[180\;,\ 190[&[190\;,\ 200[&\text{Plus de }200 \\ \text{effectifs}&40&30&10&5&2 \\ \hline \end{array}$$
1) Quelle est la dernière classe sachant que toutes les classes ont la même amplitude ?
2) Quelle est en pourcentage, la proportion d'individus mesurant au moins de $185\;cm$ ?
3) Quelle est en pourcentage, la proportion d'individus mesurant plus de $200\;cm$ ?
Exercice 8
$$\begin{array}{ccccccccc} 10 & 8 & 7 & 14 & 15 & 16 & 12 & 9 & 11 \\ 13 & 11 & 12 & 6 & 5 & 13 & 14 & 12 & 19 \\ 11 & 18 & 6 & 6 & 7 & 8 & 9 & 11 & 8 \\ 13 & 14 & 15 & 8 & 8 & 8 & 10 & 10 & 11 \\ 11 & 12 & 13 & 14 & 9 & 10 & 6 & 18 & 7 \\ 4 & 4 & 5 & 5 & 10 & & & & \end{array}$$
1) Regrouper ces $50$ notes dans des classes d'égale amplitude $2$ et dresser le tableau statistique contenant les classes, les milieux $x_{i}$ des classes, les effectifs, les effectifs cumulés croissants, les effectifs cumulés décroissants.
2) Calculer la moyenne $\overline{x}$ de cette série
3) Construire l'histogramme de cette série
4) Quel est le nombre de candidats ayant obtenu une note strictement supérieure à $15$ ?
5) Quel est le nombre de candidats ayant obtenu une note au moins égale à $10$ ?
6) Quel est le nombre de candidats ayant obtenu une note appartenant à $]5\;,\ 20[$ ?
Exercice 9
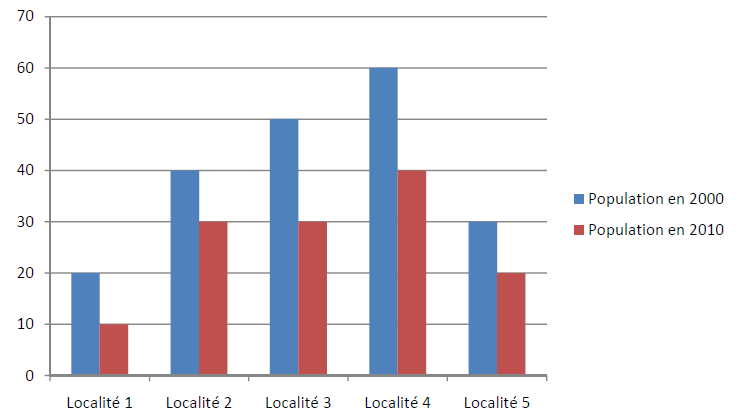
Cette étude avait pour objectif d'étudier l'effet de l'exode sur les populations rurales.
Quelles sont les localités qui ont le plus souffert de l'exode rural ?
Exercice 10
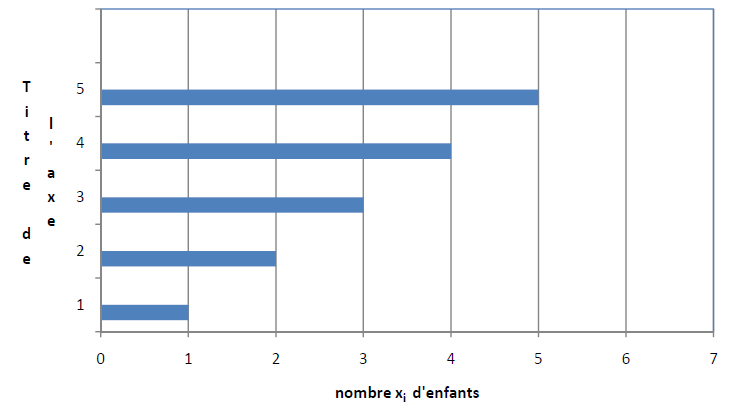
1) Quels sont les individus de la population ?
2) Quel est :
a) Le caractère étudié ?
b) L'effectif total ?
c) Les valeurs $x_{i}$ du caractère ?
d) Les effectifs partiels ?
e) Le mode de cette série ?
3) Dresser le tableau des effectifs
4) Calculer et interpréter la moyenne $\overline{x}$, puis la variance $V(X)$.
5) Déterminer les quartiles $Q_{1}\;,\ Q_{2}\;,\text{ et }Q_{3}$ de cette série statistique et en construire le diagramme en boite
6) Calculer le coefficient de variation, l'écart absolu moyen par rapport à la moyenne, l'écart interquartile
Exercice 11
$$\begin{array}{|c|c|c|c|c|c|} \hline \text{Classes}&[0\;,\ 5[&[5\;,\ 10[&[10\;,\ 15[&[15\;,\ 20[&[20\;,\ 25[ \\ \hline \text{Effectifs}&10&20&10&5&5 \\ \hline \end{array}$$
1) Construire l'histogramme des fréquences correspondant à ce tableau statistique et le polygone des fréquences
2) Construire la courbe des fréquences cumulées croissantes et la courbe des fréquences cumulées décroissantes
Donner par lecture graphique la médiane $M_{e}$ de cette série statistique
3) Calculer la moyenne $\overline{x}$ et l'écart type de cette série statistique
4) Déterminer par le calcul les quartiles de cette série statistique
Exercice 12
$$\begin{array}{|c|c|c|c|c|c|} \hline \text{Classes}&[0\;,\ 4[&[4\;,\ 6[&[6\;,\ 8[&[8\;,\ 12[&[12\;,\ 17[ \\ \hline \text{Effectifs }n_{i}&20&10&5&5&10 \\ \hline \end{array}$$
1) Calculer l'amplitude $a_{i}$ et la densité $d_{i}$ de chaque classe $[C_{i}\;,\ C_{i+1}[$
2) Construire l'histogramme des effectifs de cette série statistique
3) Quelle est la classe modale ?
4) Calculer la moyenne $\overline{x}$ et la variance $V(X)$ de cette série statistique.
5) Déterminer par le calcul les quartiles de cette série statistique
Exercice 13
$3\;,\ 5\;,\ 9\;,\ 9\;,\ 9\;,\ 10\;,\ 7\;,\ 8\;,\ 3\;,\ 6$
1) Calculer la moyenne $\overline{x}$ de ce candidat
2) Déterminer la note médiane
Exercice 14
$5\;cm\;,\ 6\;cm\;,\ 6\;cm\;,\ 8\;cm\;,\text{ et }10\;cm.$
1) Déterminer l'aire moyenne de ces terrains et en déduire le coté moyen
$\overline{C}$ à $10^{-2}$ près par excès
2) Calculer le coté moyen $\overline{C}$ d'une autre façon
3) Déterminer le coté médian de ces terrains
Exercices 15
$$\begin{array}{|c|c|c|c|c|c|c|c|c|} \hline x_{i}&1&2&4&5&6&8&9&10 \\ \hline n_{i}&10&12&11&13&15&20&14&5 \\ \hline \end{array}$$
Calculer la moyenne $\overline{x}$, la variance $V(X)$ et la médiane de cette série statistique
Exercice 16
$$\begin{array}{|c|c|c|c|c|c|} \hline \text{Classes}&[10\;,\ 20[&[20\;,\ 30[&[30\;,\ 40[&[40\;,\ 50[&[50\;,\ 60[ \\ \hline \text{Effectifs}&10&20&10&5&5 \\ \hline \end{array}$$
1) Déterminer la classe nodale
2) Calculer les quartiles de cette série statistique
Exercice 17
Lors d'un $6^{eme}$ devoir, cet élève a obtenu la note de $17$ sur $20$
Quelle est la moyenne de cet élève sur l'ensemble des $6$ devoirs ?
Exercice 18
Quelle est la moyenne de cet élève sur l'ensemble des $5$ notes ?
Exercice 19
$$\begin{array}{|c|c|c|c|c|c|c|c|c|} \hline x_{i}&200&300&500&600&800&900&1000&1200 \\ \hline n_{i}&10&15&15&20&5&8&12&15 \\ \hline \end{array}$$
On pose $y_{i}=x_{i}-700$
1) Calculer $\overline{y}$ et en déduire $\overline{x}$
2) Calculer la variance $V(Y)$ et en déduire la variance $V(X)$
Exercice 20
Une $2^{ième}$ série de $13$ observations a donné une moyenne de $6$ et une variance de $8$
Les $7$ valeurs de $X$ lors de la première série d'observation sont notées
$x_{1}\;,\ x_{2}\;,\ x_{3}\;,\ x_{4}\;,\ x_{5}\;,\ x_{6}\text{ et }x_{7}$
et les valeurs de $X$ lors de le $2^{eme}$ série d'observations sont notées
$x_{8}\;,\ x_{9}\;,\ x_{10}\;,\ x_{11}\;,\ x_{12}\;,\ x_{13}\;,\ x_{14}\;,\ x_{15}\;,\ x_{16}\;,\ x_{17}\;,\ x_{18}\;,\ x_{19}\text{ et }x_{20}$
1) En utilisant la formule de Koenig pour chaque série d'observations montrer que :
$$\sum_{i=1}^{7}\;x_{i}^{2}=217\text{ et }\sum_{i=8}^{20}\;x_{i}^{2}=572$$
2) Montrer que la moyenne de $X\text{ est }\dfrac{113}{20}$
3) Montrer que la variance de $X\text{ est de }V(X)=\dfrac{3011}{400}$
Exercice 21
$$\begin{array}{|c|c|c|c|c|c|c|c|c|} \hline x_{i}&1500&2000&2500&3000&3500&4000&4500&5000 \\ \hline n_{i}&130&350&210&130&90&50&30&10 \\ \hline \end{array}$$
On pose $y_{i}=\dfrac{x_{i}-2500}{500}$ pour $i$ allant de 1 à 8.
1) Dresser le tableau statistique de la série statistique des $(y_{i}\;,\ n_{i})$ pour $i$ allant de 1 à 8.
2) Calculer le moyenne $\overline{y}$ de la série des $(y_{i}\;,\ n_{i})$
et en déduire $\overline{x}$ de la série des $(x_{i}\;,\ n_{i})$
3) Calculer la variance $V(Y)$ et en déduire la variance $V(X)$.
4) Déterminer la médiane de la série des $(x_{i}\;,\ n_{i})$
5) Calculer l'écart absolu moyen de la série des $(x_{i}\;,\ n_{i})$, par rapport à la moyenne $\overline{x}$
6) Calculer l'écart absolu moyen de la série des $(x_{i}\;,\ n_{i})$, par rapport à la médiane $M_{2}$
Exercice 22
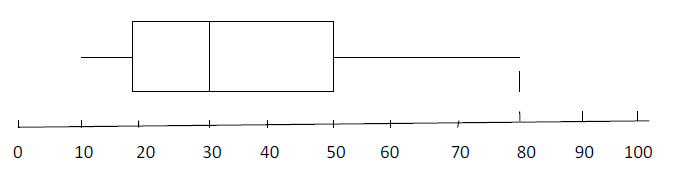
Déterminer :
1) La plus petite et la plus grande valeur du caractère
2) L'étendue de la série
3) Les quartiles de cette série
4) L'intervalle interquartile
Exercice 23
$$\begin{array}{|c|c|c|c|c|c|c|} \hline y\backslash x &2&6&10&14&18&22 \\ \hline 75&a&5&0&0&0&0 \\ \hline 125&0&7&1&0&2&0 \\ \hline 175&2&0&9&8&15&4 \\ \hline 225&0&1&0&3&b&1 \\ \hline \end{array}$$
1) Déterminer $a\text{ et }b$ pour que la moyenne de $1^{ere}$ série marginale $X$ soit $\overline{x}=\dfrac{996}{59}$ et la moyenne de la $2^{eme}$ série marginale $Y$ soit $\overline{y}=\dfrac{8450}{59}$
2) Donner les valeurs $n_{11}\;,\ n_{36}\;,\ n_{5}\;,\ n_{4}$
3) Donner l'effectif total $N$ de cette série statistique double
4) a) Établir le tableau des effectifs de le première série marginale $X$ et celui de la deuxième série marginale $Y$
b) calculer les variances marginales $V(X)\text{ et }V(Y)$
5) Calculer :
a) Le salaire moyen $m_{1}$ des ouvriers qui ont $2$ années d'exercices
b) La fréquence du salaire $125$ milles francs sachant que c'est lui d'un ouvrier qui a $6$ ans d'exercices
c) La fréquence des ouvriers qui ont $18$ ans d'exercices sachant qu'ils ont un salaire de $175$ milles francs
d) Le nombre moyen d'années d'exercices des ouvriers qui ont un salaire de $225$ milles francs
e) Calculer la fréquence des individus qui ont $6$ ans d'exercices et un salaire de $125$ milles francs
f) Dresser le tableau statistique de la série conditionnelle $Y/X=x_{2}$ et celui de la série conditionnelle $X/Y=y_{3}$
Exercice 24
$$\begin{array}{|c|c|c|c|c|c|} \hline x\backslash y & 3 & 6 & 7 & 8 & \text{Total} \\ \hline 2 & 5 & 4 & & & 16 \\ \hline 3 & & 3 & 4 & 3 & \\ \hline 4 & 3 & 5 & 2 & & 12 \\ \hline \text{Total} & 10 & & 11 & & 40 \\ \hline \end{array}$$
2) Calculer
$$f\dfrac{x_{2}}{y_{2}}\;,\ f_{2}\;,\ f_{3}\;,\ f\dfrac{y_{3}}{x_{1}}\;,\ f_{23}\text{ et }f_{32}$$
3) $X\text{ et }Y$ sont-ils indépendants ?
Exercice 25
$$\begin{array}{|c|c|c|c|c|c|} \hline x\backslash y & 10 & 30 & 40 & 50 & \text{Total} \\ \hline 2 & & & & & 0.45 \\ \hline 3 & & & & & 0.55 \\ \hline \text{Total} & 0.1 & 0.3 & 0.4 & 0.2 & 1 \\ \hline \end{array}$$
Exercice 26
$$\begin{array}{|c|c|c|c|} \hline x\backslash y & 12 & 13 & 15 \\ \hline 5 & 8 & 12 & 2 \\ \hline 7 & & 24 & \\ \hline 8 & & & 5 \\ \hline \end{array}$$
Exercice 27
$$\begin{array}{|c|c|c|c|c|c|} \hline x\backslash y & [0\;,\ 4[ & [4\;,\ 8[ & [8\;,\ 12[ & [12\;,\ 16[ & [16\;,\ 20[ \\ \hline [0\;,\ 4[ & 2 & 5 & 2 & 0 & 0 \\ \hline [4\;,\ 8[ & 1 & 12 & 10 & 3 & 0 \\ \hline [8\;,\ 12[ & 0 & 3 & 28 & 12 & 1 \\ \hline [12\;,\ 16[ & 0 & 1 & 5 & 10 & 2 \\ \hline [16\;,\ 20[ & 0 & 0 & 0 & 1 & 2 \\ \hline \end{array}$$
1) Représenter graphiquement la série statistique double $(X\;,\ Y)$ par un nuage de points $M_{ij}(x_{i}\;,\ y_{j})$ pondère par $n_{ij}$
2) Déterminer les séries marginales $X\text{ et }Y$ et calculer les moyennes marginales $x\text{ et }y$ et les variances marginales $V(X)\text{ et }V(Y)$
3) Déterminer les distributions conditionnelles de $X$ liées par $Y$
Déterminer les distributions conditionnelles de $Y$ liées par $X$
Calculer toutes les moyennes et toutes les variances conditionnelles.
4) Déterminer la distribution des moyennes conditionnelles $m_{i}$ de $Y$ liées par $X.$
Calculer sa moyenne et sa variance
5) Déterminer la distribution des variances conditionnelles $V_{i}$ de $Y$ liées par $X$ et calculer sa moyenne

Ajouter un commentaire