Bac maths, Antilles 2004
Classe:
Terminale
Barycentre espace :
5 points
On considère le tétraèdre $ABCD$ ; on note $I$ le milieu du segment $[AB]\ $ et $\ J$ celui de $[CD].$
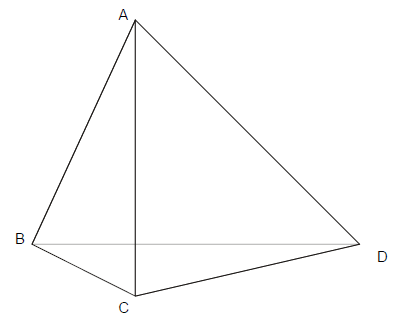
1. a. Soit $G_{1}$ le barycentre du système de points pondérés $$\{(A\;,\ 1)\;;\ (B\;,\ 1)\;;\ (C\;,\ -1)\;;\ (D\;,\ 1)\}$$
Exprimer $\overrightarrow{IG}_{1}$ en fonction de $\overrightarrow{CD}.$
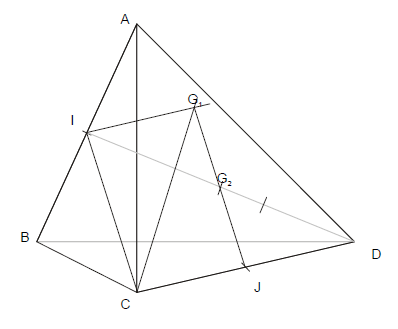
Placez $I\;,\ J$, et $G_{1}$ sur la figure.
b. Soit $G_{2}$ le barycentre du système de points pondérés $\{(A\;,\ 1)\;;\ (B\;,\ 1)\;;\ (D\;,\ 2)\}.$
Démontrez que $G_{2}$ est le milieu du segment $[ID]$. Placez $G_{2}.$
c. Démontrez que $IG_{1}DJ$ est un parallélogramme. En déduire la position de $G_{2}$ par rapport aux points $G_{1}$ et $J.$
2. Soit $m$ un réel. On note $G_{m}$ le barycentre du système de points pondérés $$\{(A\;,\ 1)\;;\ (B\;,\ 1)\;; (C\;,\ m-2)\;;\ (D\;,\ m)\}$$
a. Précisez l'ensemble $E$ des valeurs de $m$ pour lesquelles le barycentre $G_{m}$ existe.
Dans les questions qui suivent, on suppose que le réel $m$ appartient à l'ensemble $E.$
b. Démontrez que $G_{m}$ appartient au plan $(ICD)$.
c. Démontrez que le vecteur $m\overrightarrow{JG}_{m}$ est constant.
d. En déduire l'ensemble $F$des points $G_{m}$ lorsque $m$ décrit l'ensemble $E.$
Correction
$G_{1}\ :\ \{(A\;;\ 1)\;;\ (B\;;\ 1)\;;\ (C\;;\ -1)\;;\ (D\;;\ 1)\}$
1. a. On a, quel que soit le point $M$ : $$\overrightarrow{MA}+\overrightarrow{MB}-\overrightarrow{MC}+\overrightarrow{MD}=2\overrightarrow{MG}_{1}$$
et en remplaçant $M$ par $I$, on obtient :
$\begin{array}{rcl} \overrightarrow{IA}+\overrightarrow{IB}-\overrightarrow{IC}+\overrightarrow{ID}=2\overrightarrow{IG}_{1}&\Leftrightarrow&\overrightarrow{CD}=2\overrightarrow{IG}_{1} \\ \\ &\Leftrightarrow&\overrightarrow{IG}_{1}=\dfrac{1}{2}\overrightarrow{CD}\end{array}$
b. $G_{2}\ :\ \{(A\;;\ 1)\;;\ (B\;;\ 1)\;;\ (D\;;\ 2)\}$. On a quel que soit le point $M$ du plan : $$\overrightarrow{MA}+\overrightarrow{MB}+2\overrightarrow{MD}=4\overrightarrow{MG}_{2}$$
et en remplaçant $M$ par $I$, on obtient :
$\begin{array}{rcl} \overrightarrow{IA}+\overrightarrow{IB}+2\overrightarrow{ID}=4\overrightarrow{IG}_{2}&\Leftrightarrow&\overrightarrow{ID}=2\overrightarrow{IG}_{2} \\ \\ &\Leftrightarrow&\overrightarrow{IG}_{2}=\dfrac{1}{2}\overrightarrow{ID}\end{array}$
c. D'après la question 1. a. on a $\overrightarrow{IG}_{1}=\dfrac{1}{2}\overrightarrow{CD}=\overrightarrow{CJ}=\overrightarrow{JD}$ donc $IG_{1}DJ$ est un parallélogramme.
Ses diagonales se coupent en leur milieu, or on sait que $G_{2}$ est le milieu de $[ID]$, c'est donc aussi le milieu de $[JG_{1}].$
2. a. Le barycentre existe si et seulement si la somme des coefficients n'est pas nulle. Elle est nulle quand $1+1+m-2+m=0$, c'est-à-dire quand $m=0.$
b. $G_{m}\ :\ \{(A\;;\ 1)\;;\ (B\;;\ 1)\;;\ (C\;;\ m-2)\;;\ (D\;;\ m)\}$. Quel que soit $M$ du plan, on a : $$\overrightarrow{MA}+\overrightarrow{MB}+(m-2)\overrightarrow{MC}+m\overrightarrow{MD}=2m\overrightarrow{MG}_{m}$$
et en remplaçant $M$ par $I$ : $$\overrightarrow{IA}+\overrightarrow{IB}+(m-2)\overrightarrow{IC}+m\overrightarrow{ID}=2m\overrightarrow{IG}_{m}$$ ou encore $$(m-2)\overrightarrow{IC}+m\overrightarrow{ID}=2m\overrightarrow{IG}_{m}$$ c'est-à-dire $IG_{m}$ est une combinaison linéaire des vecteurs $\overrightarrow{IC}$ et $\overrightarrow{ID}$
,
donc le point $G_{m}$ est un point du plan $(ICD).$
c. $$\overrightarrow{MA}+\overrightarrow{MB}+(m-2)\overrightarrow{MC}+m\overrightarrow{MD}=2m\overrightarrow{MG}_{m}$$ en remplaçant $M$ par $J$ on obtient : $$\overrightarrow{JA}+\overrightarrow{JB}+(m-2)\overrightarrow{JC}+m\overrightarrow{JD}=2m\overrightarrow{JG}_{m}$$ ou encore $$\overrightarrow{JA}+\overrightarrow{JB}-2\overrightarrow{JC}+m\overrightarrow{JC}+m\overrightarrow{JD}=2m\overrightarrow{JG}_{m}$$
Or, $J$ est le milieu de $[CD]$ donc on obtient enfin :
$\begin{array}{rcl} \overrightarrow{JA}+\overrightarrow{JB}-2\overrightarrow{JC}=2m\overrightarrow{JG}_{m}&\Leftrightarrow&m\overrightarrow{JG}_{m}=\dfrac{1}{2}(\overrightarrow{JA}+\overrightarrow{JB})-\overrightarrow{JC} \\ \\ &\Leftrightarrow&m\overrightarrow{JG}_{m}=\overrightarrow{JI}-\overrightarrow{JC} \\ \\ &\Leftrightarrow&m\overrightarrow{JG}_{m}=\overrightarrow{JI}+\overrightarrow{CJ} \\ \\ &\Leftrightarrow&m\overrightarrow{JG}_{m}=\overrightarrow{CI}\end{array}$
d. On a : $ m\overrightarrow{JG}_{m}=\overrightarrow{CI}=\overrightarrow{JG_{1}}$ ; d'après les questions précédentes. Ceci signifie que les points $G_{m}$ se trouvent sur la droite $(JG_{1}).$

Ajouter un commentaire