Devoir n°13 - 1e S1
Classe:
Première
Exercice 1
1) Résoudre et discuter l'équation d'inconnue $x$ dans $\mathbb{R}$ : $$\dfrac{x^{2}-3}{2x^{2}+1}=y\;,\quad\text{où }y\ \text{ est un réel donné}$$
2) En déduire deux parties $E$ et $F$ de $\mathbb{R}\;$, les plus grandes possibles, pour que l'application \begin{eqnarray} f\ :\ E&\longrightarrow&F\nonumber \\ x&\longmapsto&\dfrac{x^{2}-3}{2x^{2}+1}\nonumber \end{eqnarray}
soit bijective. Déterminer alors l'application réciproque $f^{-1}.$
Exercice 2
On considère les fonctions numériques $f\;,\ g$ et $h$ définies par : $$f(x)=\dfrac{x+1}{x-1}\;,\quad g(x)=\dfrac{2x}{x+2}\;,\quad h(x)=\dfrac{3-x}{1+2x}$$
1) Déterminer l'ensemble de définition de chacune des fonctions : $$g\circ f\;,\quad h\circ g\;,\quad h\circ g\circ f$$
2) Calculer $(g\circ f)(x)\;,\ (h\circ g)(x)$ et $(h\circ g\circ f)(x).$
Exercice 3
1) Préciser les ensembles de définition des fonctions $f$ définies par :
a) $f(x)=\sqrt{\dfrac{1-|x|}{2-|x|}}\qquad$ b) $f(x)=\dfrac{x^{2}+3}{x^{2}+|x|}$
c) $f(x)=\sqrt{\dfrac{1-x}{x}}-\sqrt{\dfrac{1+x}{2-x}}\qquad$ d) $f(x)=\dfrac{1}{\sqrt{-x^{2}+6x+9}}$
2) Démontrer que chacune des fonctions suivantes est bornée :
a) \begin{eqnarray} f\ :\ [-3\;;\ 0]&\longrightarrow&\mathbb{R}\nonumber \\ x&\longmapsto&\dfrac{-1}{2x-1}\nonumber \end{eqnarray}
b) \begin{eqnarray} f\ :\ \mathbb{R}&\longrightarrow&\mathbb{R}\nonumber \\ x&\longmapsto&\dfrac{|x|}{\sqrt{x^{2}+1}}\nonumber \end{eqnarray}
c) \begin{eqnarray} f\ :\ [-2\;;\ 2]&\longrightarrow&\mathbb{R}\nonumber \\ x&\longmapsto&|x+1|-|2x-1|\nonumber \end{eqnarray}
Exercice 4
Une plaque P est constituée par la réunion de deux carrés de côté 6 et d'un triangle rectangle isocèle $ABC.$
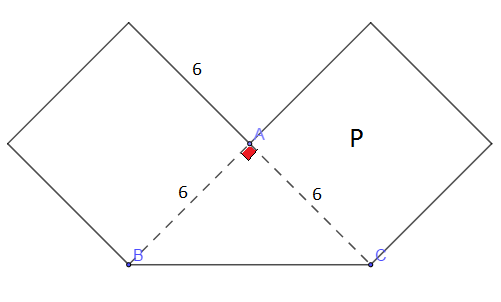
Calculer à quelle distance du milieu $O$ de $[BC]$ se troue le centre d'inertie $G$ de la plaque.
Exercice 5
Étant donné un parallélogramme $ABCD$, on construit les points $P\;,\ Q$ et $R$ définis par : $$\centerdot\ \overrightarrow{AP}=\dfrac{2}{3}\overrightarrow{AB}\;,\quad\centerdot\ \overrightarrow{AR}=\dfrac{3}{4}\overrightarrow{AD}\;,\quad\centerdot\ PARQ\text{ est un parallélogramme}$$
Il s'agit d'établir ce que suggère la figure ci-dessus, à savoir que les droites $(BR)\;,\ (CQ)$ et $(DP)$ sont concourantes.
1) Exprimer $P$ comme barycentre de $A$ et $B\;,\ R$ comme barycentre de $A$ et $D$ et montrer que $(BR)$ et $(DP)$ sont sécantes en $I$ barycentre de $(A\;,\ 1)\;,\ (B\;,\ 2)$ et $(D\;,\ 3).$
Indication : on pourra établir que $I\;,\ B$ et $R$ d'une part, et $I\;,\ D$ et $P$ d'autre part, sont alignés.
2) Prouver que $Q$ est le barycentre de $\{(A\;,\ -5)(B\;,\ 8)(D\;,\ 9)\}.$
En déduire que $Q$ est le milieu de $[IC]$ (d'où, par suite, l'alignement de $I\;,\ C$ et $Q).$
$$\text{Durée : 4 h}$$
Auteur:
Mouhamadou Ka

Ajouter un commentaire