Devoir n° 6 - 1e S2
Classe:
Première
Exercice 1 (7 points)
1) Résoudre dans $\mathbb{R}$ l'équation : $4x^{3}-3x-1=0\quad (E).$
2) On considère l'équation $(E')$ suivante : $4x^{3}-12x^{2}+9x-2=0\quad (E').$
On pose $x=y+h.$
a) En remplaçant $x$ par $y+h$ dans $(E')\;$, on obtient une nouvelle équation $(E'')$ dans laquelle $y$ est l'inconnue.
Quelle valeur faut-il donner à $h$ pour que le coefficient de $y^{2}$ dans $(E'')$ soit nul ?
b) $h$ ayant la valeur trouvée en a) , résoudre $(E'')$ puis $(E').$
3) Résoudre dans $\mathbb{R}$ l'inéquation : $$\dfrac{4x^{3}-3x-1}{x+1}\geq 0$$
Exercice 2 (6 points)
Résoudre dans $\mathbb{R}$ les équations ou inéquations :
a) $\sqrt{-x^{2}+x+1}<x-5$
b) $\sqrt{-4x^{2}+x+5}\leq 2x+2$
c) $x^{2}+x+\dfrac{1}{x}+\dfrac{1}{x^{2}}-4=0$ (on posera $X=x+\dfrac{1}{x}$ et on pourra calculer $X^{2}).$
Exercice 3 (3 points)
Le plan est rapporté à un repère orthonormé direct $(O\;,\ \vec{i}\;,\ \vec{j}).$ Soit $(\mathcal{C})$ le cercle trigonométrique de centre $O_;;\ I$ et $J$ les points de $(\mathcal{C})$ tels que : $\overrightarrow{OI}=\vec{i}$ et $\overrightarrow{OJ}=\vec{j}$ (voir figure ci-dessous).
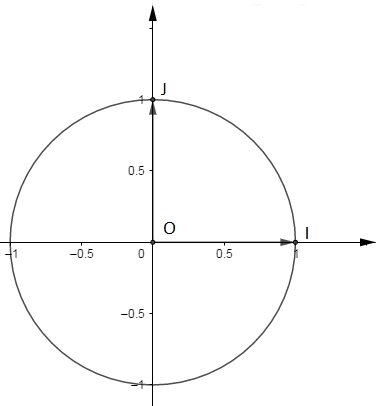
1) Placer les points $M$ et $N\;$, images respectives sur $(\mathcal{C})$ des réels $\dfrac{273\pi}{6}$ et $-\dfrac{207\pi}{4}.$
2) Donner la mesure principale de chacun des angles orientés
$(\overrightarrow{OM}\;,\ \overrightarrow{ON})\;,\ (\overrightarrow{OM}\;,\ \overrightarrow{OI})\;,\ (\overrightarrow{ON}\;,\ \overrightarrow{OJ})$ et $(\overrightarrow{OJ}\;,\ \overrightarrow{OM}).$
Exercice 4 (4 points)
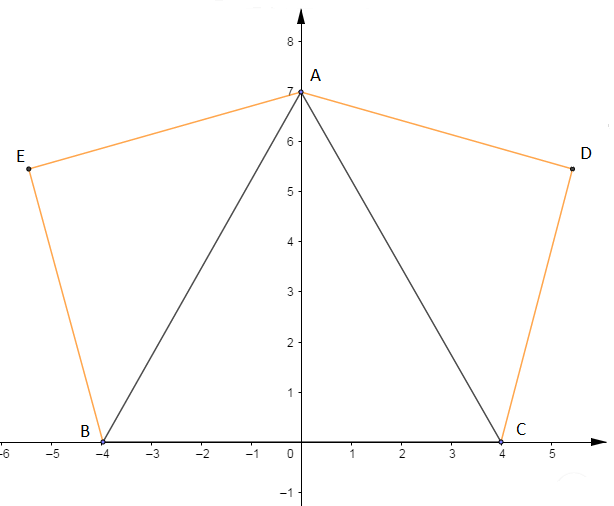
Soit $ABC$ un triangle équilatéral direct, $ADC$ et $AEB$ des triangles rectangles isocèles tels que indiqués sur la figure ci-dessus.
Donner la mesure principale en radians des angles orientés suivants :
$(\overrightarrow{AB}\;,\ \overrightarrow{AC})\;,\ (\overrightarrow{DC}\;,\ \overrightarrow{DA})\;,\ (\overrightarrow{EB}\;,\ \overrightarrow{EA})\;,\ (\overrightarrow{CB}\;,\ \overrightarrow{CD})$
$(\overrightarrow{AE}\;,\ \overrightarrow{AD})\;,\ (\overrightarrow{BC}\;,\ \overrightarrow{BE})\;,\ (\overrightarrow{BE}\;,\ \overrightarrow{BD})$ et $(\overrightarrow{EB}\;,\ \overrightarrow{BD}).$
N.B. Les réponses devront être justifiées.
Auteur:
Mouhamadou Ka

Ajouter un commentaire