Énergie nucléaire : réactions spontanées, fusion et fission - TL
Classe:
Terminale
I. Le noyau
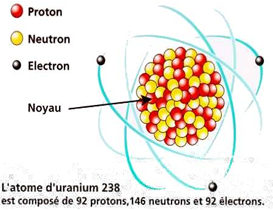
1. Constituants du noyau
Le noyau d'un atome est formé de particules appelés nucléons qui sont de deux sortes : les protons et les neutrons.
Le proton est une particule de masse $m_{p}=1.672\cdot 10^{-27}kg$ et de charge $q_{p}=1.6\cdot 10^{-19}C$
Le neutron est une particule de masse $m_{n}=1.674\cdot 10^{-27}Kg$ sensiblement et de charge nulle.
2. Nucléide
On appelle nucléide la famille de noyaux caractérisés par un nombre donné de protons et un nombre donné de neutrons.
Les noyaux d'un nucléide ont :
$-\ $le même nombre de masse $A$
$-\ $le même de charge $Z$
On le représente par : $_{Z}^{A}X$ où $X$ est le symbole de l'élément
Exemples :
$_{1}^{1}H$, $_{2}^{4}He$, $_{6}^{12}C$, $_{8}^{16}O$, $_{1}^{2}H$, $_{1}^{3}H$, $_{7}^{14}N$, $_{26}^{56}Fe$, $_{9}^{19}F$,
3. Isotopie
Des atomes possédant le même numéro atomique, (même nombre de protons) mais de masse atomique différente (nombre différent de neutrons) sont appelés isotopes.
4. Énergie de masse
4.1. Formule d'Einstein
Elle s'exprime l'équivalence entre la masse et l'énergie :$$\boxed{E=mc^{2}}$$
$E$ en joules $(J)$
$m$ en mètres $(m)$
$c$ en mètres par seconde $\left(m\cdot s^{-1}\right)$
4.2. Défaut de masse
La masse du noyau $m_{X}$ est toujours inférieure à la masse des nucléons qui le constituent $$\boxed{\Delta m=Zm_{p}+(A-Z)m_{n}-m_{X}}$$
La différence de masse est appelée défaut de masse.
On appelle défaut de masse d'un noyau, la différence entre la masse des nucléons séparés au repos et la masse du noyau du noyau au repos.
4.3. Unité de masse atomique
Le kilogramme $(kg)$ n'est pas pratique d'utilisation à l'échelle microscopique.
On utilise alors une unité plus appropriée : l'unité de masse atomique.
L'unité de masse atomique $($symbole : $u)$ est le douzième de la masse d'un atome de carbone
$\begin{array}{rcl} 1u&=&\dfrac{1}{12}\dfrac{12\cdot 10^{-3}}{N_{A}}\\&=&\dfrac{10^{-3}}{N_{A}}\dfrac{10^{-3}}{6.02\cdot 10^{23}}\\\Rightarrow\boxed{1u\approx 1.66\cdot 10^{-27}kg} \end{array}$
En première approximation, les masses des noyaux sont voisines de multiple entier de la masse atomique
Exemple :
$M\left(_{17}^{35}Cl\right)=34.958u\approx35u$
5. Stabilité du noyau
5.1. Énergie de liaison : relation d'Einstein
On appelle énergie de liaison d'un noyau, l'énergie qu'il faut fournir à un noyau au repos pour le dissocier en nucléons séparés au repos
Pour un noyau $_{Z}^{A}X$ $$\boxed{E_{l}=\left(Zm_{p}+(A-Z)m_{n}-m_{X}\right)c^{2}}$$
On exprime également l'énergie de liaison du noyau en mégaélectronvolt $(MeV)$
Remarque
On peut alors exprimer les masses en leur équivalent énergétique d'après la relation précédente $1u=931.MeV/c^{2}$
$$\begin{array}{|l|c|c|c|} \hline\text{particules}&p^{+}&n^{0}&e^{-}\\ \hline \text{charge}&+e&0&-e\\ \hline m(u)&1.0073u&1.0087u&0.55^{\ast}10^{-3}u\\ \hline m\left(MeV/c^{2}\right)&938.280&939.573&0.511003\\ \hline \end{array}$$
De manière générale, à toute variation de masse d'un système correspond une variation d'énergie :$$\boxed{\Delta E=\Delta mc^{2}}$$
Cette relation constitue la relation d'Einstein
5.2. Énergie de liaison par nucléon
Pour comparer les différents noyaux entre, on définit l'énergie de liaison par nucléon.
C'est l'énergie à fournir à un noyau pour lui arracher un nucléon $$\boxed{E_{A}=\dfrac{E_{1}}{A}}$$
5.3. Stabilité du noyau : courbe d'Aston
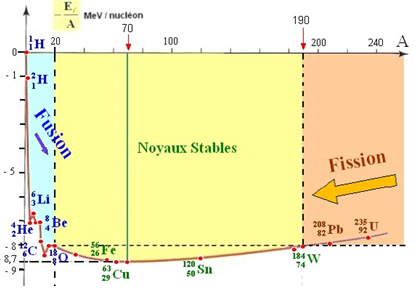
Ce graphe donne les valeurs moyennes de l'énergie de liaison par nucléon $E_{1}$ en fonction du nombre de masse $A$ : cette est appelée courbe d'Aston
$\bullet\ $Pour les noyaux dont le nombre de masse est compris entre $50$ et $80$, la courbe présente un minimum aplati qui correspond aux noyaux les plus stables $\left(E_{A}=-8.7eV\right).$
$\bullet\ $Les extrémités de la courbe correspondent aux noyaux instables :
$-\ $un noyau lourd $(A\succ 100)$ peut se casser en des noyaux stables pour gagner en stabilité
$-\ $des noyaux légers, pour gagner en stabilité, peuvent s'unir pour donner des noyaux stables.
Il existe, d'après la courbe d'Aston, deux façons possibles d'extraire de l'énergie : ou bien fusionner des noyaux légers ou fissionner des noyaux lourds pour avoir des noyaux stables
II. La radioactivité
Les noyaux contiennent des protons chargés positivement, qui devraient se repousser d'après l'interaction électromagnétique.
Pour expliquer la cohésion des noyaux, on admet l'existence d'une interaction attractive qui unit l'ensemble des nucléons et qui prédomine (aux courtes distances) devant l'interaction électromagnétique : c'est l'interaction forte
Cependant, dans certains cas, la cohésion est insuffisante : les noyaux sont instables et se désintègrent spontanément : ils sont radioactifs
1. Définition
La radioactivité est la désintégration spontanée d'un noyau en un autre noyau, accompagnée de l'émission de particules subatomiques et(ou) de rayonnement électromagnétique
2. Caractéristiques de transformations radioactives
Les transformations radioactives sont :
$\surd\ $Indépendantes de la nature des liaisons entre les atomes (combinaisonchimique) dont le noyau radioactif fait partie
Exemples :
$\left(UO_{2}\;,\ UF_{6}\ \longrightarrow\ U\text{ radioactif}\right)$
$\surd\ $indépendantes de paramètres usuels(pression, température, état physique : solide, liquide ou gazeux
$\surd\ $spontanées (elles se réalisent seules, sans intervention extérieure pour les déclencher)
$\surd\ $inéluctables (un noyau radioactif se désintègrera tôt ou tard, rien ne peut empêcher sa désintégration)
$\surd\ $aléatoires (si on « sélectionne » un noyau radioactif, il est impossible de prévoir l'instant de sa désintégration)
3. Évolution temporelle d'une substance radioactive
3.1. Loi de désintégration radioactive
Si on étudie un seul noyau, on ne sait pas quand il va se désintégrer
Le noyau ne « vieillit » pas : la probabilité de désintégration ne dépend pas du temps.
On peut étudier un ensemble de noyaux afin de réaliser des statistiques.
La probabilité qu'un noyau radioactif se désintègre pendant un intervalle de temps est donnée par la relation $$\boxed{N=\dfrac{N_{0}}{2^{n}}}$$
Courbe de décroissance radioactive $$n\,T\ \longrightarrow\ N=\dfrac{N_{0}}{2^{n}}$$
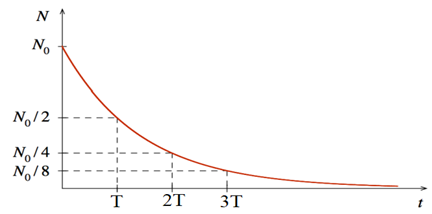
4.2. La période radioactive
La période radioactive ou demi-vie est la durée nécessaire à la désintégration de la moitié des noyaux présents initialement dans l'échantillon $$\boxed{T=\dfrac{\ln 2}{\gamma}}$$
Remarque :
Le période a une signification complètement différente de celle que nous attribuons habituellement.
Il ne s'agit pas d'un phénomène période
4.3. Activité d'un échantillon radioactif
L'activité d'une source est le nombre d'atomes désintégrés pendant l'unité de temps
$$\boxed{A=\dfrac{A_{0}}{2^{n}}}\text{ avec }A_{0}=\gamma N_{0}$$
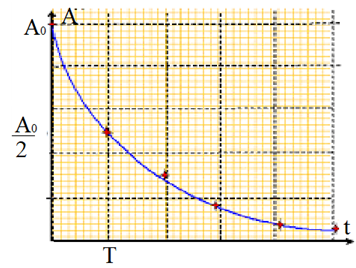
L'unité internationale de l'activité est le becquerel $\left(B_{q}\right).$
Le becquerel correspond à une désintégration par seconde.
On utilise également une ancienne unité le curie $(Ci)$ $1Ci=3.7\cdot 10^{10}Bq$
3. Analyse du rayonnement radioactif
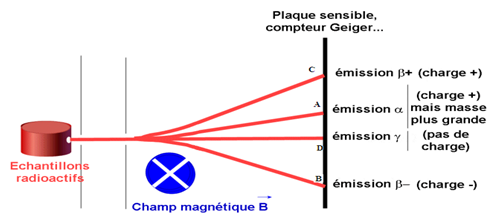
Un mélange de substances radioactives est placé dans une ceinte en plomb (le rayonnement traverse difficilement le plomb).
Une plaque photographique placée à la sortie du champ permet de détecter les impacts des rayonnements.
En présence d'un champ magnétique ou électrique, la plaque montre quatre impacts : $A$, $B$, $C$ et $D$
Les champs électrique et magnétique séparent donc les rayonnements en parties : trois déviés par les champs appelés $\alpha$, $\beta^{+}$, $\beta^{-}$ et un non dévié appelée $\lambda$
4. Les différents types radioactivités
4.1. Les lois de conservation
Lors des radioactivités $\alpha$ et $\beta$, un noyau père $X$ se transforme en un noyau fils $Y$ avec production de particules chargées $\left(\alpha\;,\ \beta^{+}\text{ ou }\beta\right)$
$$\begin{array}{ccc} _{Z}^{A}X\ \longrightarrow\ &_{Z}^{A'}Y&+\ _{z}^{a}Q\\ \text{Père}&\text{fils}&\text{particule} \end{array}$$
Les équations bilan doivent respecter (lois de Soddy) :
$\bullet\ $la conservation du nombre de masse (ou de nucléons) : $A=A'+a$
$\bullet\ $la conservation de la charge (c'est-à-dire du nombre de protons) : $Z=Z'+z$
$\bullet\ $la conservation de l'énergie : $E_{\text{total}}\left(_{Z}^{A}X\right)=E_{\text{total}}\left(_{Z}^{A'}Y\right)+E_{\text{total}}\left(_{z}^{a}Q\right)$
Définitions
Caractéristiques
lois, période.
III. Rayonnement $\alpha$, $\beta$, $\gamma$
1. Radioactivité $\alpha$
1.1. Principe
La radioactivité $\alpha$ est la transformation spontanée d'un noyau en autre noyau accompagnée d'un noyau d'hélium
Le rayonnement $\alpha$ très dangereux mais peu pénétrant : arrêté par quelques $cm$ d'air ou une feuille de papier
1.2. Équation de la réaction désintégration
$$\begin{array}{ccc}_{Z}^{A}X\ \longrightarrow\ &_{Z}^{A'}Y^{\ast}&+\ _{2}^{4}He\\ \text{Père}&\text{fils}&\text{particule }\alpha \end{array}$$
Comme toute réaction nucléaire, la désintégration $\alpha$ vérifie :
$-\ $la conservation du nombre de masse : $A=A'+4\ \Rightarrow\ A'=A-4$
$-\ $la conservation du nombre de charge : $Z=Z'+2\ \Rightarrow\ Z'=Z-2$
Généralement le noyau fils, dans un état excité, se désexcite en émettant un rayonnement $\lambda$
L'équation-bilan de désintégration s'écrit finalement : $$_{Z}^{A}X\ \longrightarrow\ _{Z-2}^{A-4}Y\ +\ _{2}^{4}He\ +\ \lambda$$
Exemple :
$$_{92}^{238}U\ \longrightarrow\ _{90}^{234}Th\ +\ _{2}^{4}He$$
Remarque :
le noyau fils se situe toujours « deux cases avant » le noyau père dans la classification périodique des éléments
1.3. Bilan énergétique
La réaction se fait avec libération d'énergie (réaction exo énergétique).
Cette énergie provient de la perte de masse $$\boxed{\Delta E=\left(m_{\lambda}+m_{\alpha}-m_{x}\right)c^{2}}$$
2. Radioactivité $\beta^{-}$
2.1. Principe
La radioactivité $\beta^{-}$ est la transformation d'un noyau en autre noyau accompagné de l'émission d'un électron et un antineutrino
L'antineutrino est une particule non chargée de masse nulle se déplaçant à la célérité de la lumière.
Cette particule intervient dans le bilan de la réaction nucléaire de façon à assurer la conservation de l'énergie et de la quantité de mouvement.
L'antineutrino possède un pouvoir de pénétration extraordinaire $($arrêtés par $35$ années lumières de plomb $!)\ldots$ ce qui rend la détection très difficile.
Le rayonnement $\beta^{-}$ pénétrant (mais moins dangereux que le rayonnement $\alpha)$, arrêtées par plusieurs mètres d'air ou quelques $mm$ d'aluminium (plexiglas)
2.2. Équation de la réaction désintégration
$\begin{array}{ccc} _{A}^{Z}X&\longrightarrow_{Z'}^{A'}Y^{\ast}&+_{-1}^{0}e\\ \text{Père}&\text{fils}&\text{particule }\beta^{-}\left(_{-1}^{0}e\right) \end{array}$
Le plus souvent dans un état excité, le noyau fils, se désexcite en émettant un rayonnement $\gamma$
L'équation-bilan de désintégration s'écrit finalement :
$_{Z}^{A}X\ \longrightarrow\ _{Z+1}^{A}Y\ + _{-1}^{0}e+\gamma+\overline{v}$
Exemple :
$_{15}^{32}P\ \longrightarrow\ _{16}^{32}S\ +\ _{-1}^{0}e\ +\ \overline{v}$
La désintégration $\beta^{-}$ se produit pour des nucléides instables trop riches en neutrons.
Elle résulte de la désintégration, dans le noyau, d'un neutron qui se transforme en un proton avec émission d'un électron et d'un antineutrino :
$_{0}^{1}n\ \longrightarrow\ _{1}^{1}p\ +\ _{-1}^{0}e\ +\ \overline{v}$
Remarque :
Le noyau fils se situe toujours « une case après » le noyau père dans la classification périodique des éléments
2.3. Bilan énergétique
La réaction se fait avec libération d'énergie (réaction exo énergétique).
Cette énergie provient de la perte de masse $$\boxed{\Delta E=\left(m_{y}+m_{\beta^{-}}-m_{x}\right)c^{2}}$$
3. Radioactivité $\beta^{+}$
3.1. Principe
La radioactivité $\beta^{+}$ est la transformation d'un noyau en autre noyau accompagné de l'émission d'un positron (ou positon) et un neutrino (antiparticule de l'antineutrino)
Le rayonnement possède $\beta^{+}$ le même pouvoir de pénétration que le rayonnement $\beta^{-}$
3.2. Équation de la réaction désintégration
$\begin{array}{ccc} _{Z}^{A}X&\longrightarrow_{Z'}^{A'}Y^{\ast}&+_{1}^{0}e\\ \text{Père}&\text{fils}&\text{particule }\beta^{+}\left(_{1}^{0}e\right) \end{array}$
La désexcitation du noyau fils s'accompagne de l'émission du rayonnement $\gamma$
L'équation bilan de la désintégration s'écrit :$$\boxed{_{Z}^{A}X\ \longrightarrow\ _{Z'}^{A'}Y^{\ast}\ +\ _{1}^{0}e+v+\gamma}$$
Exemple :
$_{15}^{30}P\ \longrightarrow\ _{14}^{30}Si\ +\ _{1}^{0}e+_{0}^{0}v+\gamma$
La radioactivité $\beta^{+}$ se produit pour des nucléides obtenus artificiellement au laboratoire.
C'est pourquoi on la qualifie de radioactivité artificielle, elle est caractéristique des noyaux trop riches en protons.
Elle résulte de la désintégration, dans le noyau, d'un proton qui se transforme en un neutron avec émission d'un positron et d'un neutrino :
$_{1}^{1}p\ \longrightarrow\ _{1}^{0}n\ +\ _{1}^{0}e+v$
3.3. Bilan énergétique
L'énergie libérée lors de la désintégration $\beta^{+}$ s'écrit :$$\boxed{\Delta E=\left(m_{y}+m_{\beta^{+}}-m_{x}\right)c^{2}}$$
4. Radioactivité
Le rayonnement $\gamma$ est l'émission d'un photon par un noyau lors du retour d'un état excité à l'état stable.
La radioactivité $\gamma$ accompagne souvent les radioactivités $\alpha$ et $\beta$
IV. Réactions nucléaires provoquées : fission et fusion
Les réactions nucléaires sont :
$\bullet\ $spontanées : elles relèvent de la radioactivité naturelle
$\bullet\ $ou provoquées : elles sont dues aux bombardements des noyaux par des projectiles
1. Réaction de transmutation
1.1. Définition
La transmutation est une réaction nucléaire provoquée au cours de laquelle un élément se transforme en un autre
Les projectiles utilisés pour réaliser les transmutations sont divers :
$-\ $neutron : particule électriquement neutre
$-\ $proton ; particule $\alpha$ : particules électriquement chargés
Certains nucléides, crées par transmutation provoquée, sont instables ; leur désintégration en noyaux fils stables définit la radioactivité artificielle
Exemples
$_{7}^{14}N\ +\ _{2}^{4}He\ \longrightarrow\ _{8}^{17}O\ +\ _{1}^{1}H$
$_{3}^{7}Li\ +\ _{1}^{1}H\ \longrightarrow\ _{2}^{4}He\ +\ _{2}^{4}He$
$_{92}^{238}U\ +\ _{0}^{1}n\ \longrightarrow\ _{92}^{239}U\ +\ \gamma$
2. Fission nucléaire
2.1. Définition
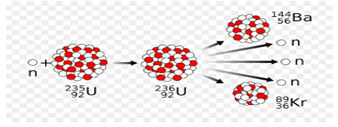
La fission est une réaction nucléaire provoquée au cours de laquelle un noyau lourd se scinde pour donner naissance à des noyaux plus légers
2.1. Bilan énergétique
Les réactions de fission sont exo énergétiques, car elles s'accompagnent d'une diminution de l'énergie de masse des noyaux réagissant
$\boxed{\Delta E=\Delta mc^{2}\quad\text{ou}\quad\Delta E=\Delta m\varepsilon_{u}\quad\text{avec}\quad\varepsilon_{u}=931.5MeV}$
Exemple
$_{92}^{235}U\ +\ _{0}^{1}n\ \longrightarrow\ _{42}^{95}Mo\ +\ _{57}^{139}La\ +\ 2_{0}^{1}n\ +\ 7_{-1}^{0}e$
$\boxed{\Delta m=m_{\text{produits}}-m_{\text{réactifs}}\ \Rightarrow\ \Delta E=\Delta m\varepsilon_{u}}$
$\boxed{\Delta E=\left(\left(m_{La}+m_{Mo}+2m_{n}+7m_{e}\right)-\left(m_{U}+m_{n}\right)\right)\varepsilon_{u}}$
$\begin{array}{rcl} \Delta E&=&\left(\left(94.8828+138.875+2\times 1.0087+7\times 0.0638\right)-\left(234.9935+1.0087\right)\right)\times931.5\\\Rightarrow\Delta E&=&-208MeV \end{array}$
2.2. Réaction en chaine
Une fission émet en moyenne $2.47$ neutrons.
Ces neutrons sont susceptibles à leur tour d'engendrer d'autres fissions.
Il en résulte une réaction en chaine.
L'énergie dégagée devient très vite considérable, sans précaution la réaction en chaine conduirait à une explosion : on obtient l'effet d'une bombe $A$
Convenablement maitrisé dans un réacteur nucléaire : cette réaction en chaine peut constituer la source d'énergie nécessaire au fonctionnement des centrales nucléaires
2. Fusion
2.1. Principe
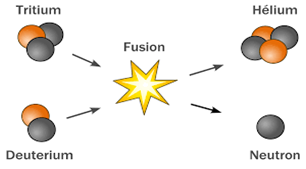
La fusion est une réaction provoquée au cours de laquelle des noyaux légers s'unissent pour donner un noyau plus lourd
2.2. Bilan énergétique
Lors de ces réactions, le bilan de masse montre qu'il y a perte de masse, donc libération d'énergie.
L'énergie libérée par la fusion appelée aussi l'énergie thermonucléaire est à l'origine du rayonnement des étoiles et du Soleil.
Lors de l'explosion des bombes thermonucléaires $($Bombe $H)$, l'énergie libérée est produite par une réaction de fusion non contrôlée
Malheureusement aujourd'hui, on ne sait ni contrôler la réaction de fusion, ni construire des réacteurs qui produiraient cette énergie de manière régulée et continue
$\boxed{\Delta E=\Delta mc^{2}\quad\text{ou}\quad\Delta E=\Delta m\varepsilon_{u}\quad\text{avec}\quad\varepsilon_{u}=931.5MeV}$
Exercice d'application
On considère la réaction nucléaire suivante :
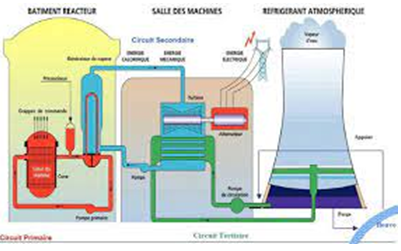
$_{1}^{2}H\ +\ _{1}^{1}\ \longrightarrow\ _{2}^{4}He\ +\ _{0}^{1}n$
Quelle énergie $($en $MeV)$ est libérée lors de la formation du noyau de l'hélium.
On donne les énergies de liaison par nucléon :
$-\ $pour le deutérium : $E\left(_{1}^{2}H\right)=1.10\,MeV$
$-\ $pour le tritium : $E\left(_{1}^{3}H\right)=2.83\,MeV$
$-\ $pour l'hélium : $E\left(_{1}^{4}He\right)=7.07\,MeV$
Solution
L'énergie libérée lors de la formation de l'hélium
$\begin{array}{rcl}\Delta E&=&\left(\left(m_{\alpha}+m_{n}\right)-\left(m_{D}+m_{T}\right)\right)c^{2}\\&=&m_{\alpha}c^{2}+m_{n}c^{2}-m_{D}c^{2}-m_{T}c^{2}\end{array}$
$\begin{array}{rcl} \text{Or}\;,\quad E_{1}&=&\left(Zm_{p}+\left(A-Z\right)m_{n}-m_{x}\right)c^{2}\\\Rightarrow\;m_{x}c^{2}&=&Zm_{p}c^{2}+\left(A-Z\right)m_{n}c^{2}-E_{1x} \end{array}$
$\begin{array}{rcl} \Delta E&=&2m_{p}c^{2}+2m_{n}c^{2}-E_{1\alpha}+m_{n}c^{2}-m_{p}c^{2}-2m_{n}c^{2}+E_{1T}-m_{p}c^{2}-m_{n}c^{2}+E_{1D}\\\Rightarrow\Delta E&=&E_{1\alpha}+E_{1T}+E_{1D}\\&=&4\times 7.07+3\times 2.83+2\times 1.01\\\Rightarrow\Delta E&=&-17.6MeV \end{array}$
L'énergie stellaire
V. Les applications
1. Centrales nucléaires
Le combustible d'une centrale nucléaire contient des atomes fissiles c'est-à-dire des atomes dont le noyau a la capacité de se casser sous l'action d'un neutron, et, ce faisant, de libérer une quantité considérable d'énergie.
D'où le nom de « combustible » par analogie avec la matière fossile brûlée dans une centrale thermique classique.
Les principaux atomes fissiles sont l'uranium $233$, l'uranium $235$, le plutonium $239$ et le plutonium $241.$
Seul l'uranium $235$ se trouve à l'état naturel.
C'est donc le plus souvent lui qui est utilisé comme combustible dans les centrales nucléaires.

2. Datation
La datation par le carbone $14$ dans le temps, mais pas plus de $30.000\text{ ans.}$
D'autres nucléides tels que le potassium $_{19}^{40}K$ sont utilisés pour la datation
3. Traceur
Les isotopes de même élément ayant des propriétés chimiques identiques ; on ne modifie pas le comportement chimique d'un isotope stable en le remplaçant par un isotope radioactif.
C'est le principe des traceurs et marqueurs radioactifs dont on connait de nombreuses applications.
$\bullet\ $En chimie, l'étude cinétique de certaines réactions s'appuie sur la mesure des rayonnements émis par des noyaux radioactifs.
Le marquage des molécules organiques par introduction par un atome de carbone $14$ en position connue est utilisé pour analyser les mécanismes réactionnels de la chimie organique
$\bullet\ $En biologie,certains phénomènes métaboliques sont étudiés par des types de marquage des mécanismes de biosynthèse
$\bullet\ $En médecine,les traceurs radioactifs sont utilisés à des fins diagnostics : étude du fonctionnement de la glande thyroïde à l'iode $131$, détermination de certaines anémies

Ajouter un commentaire