Aspect ondulatoire de la lumière - TL
Classe:
Terminale
I. Émission - Réception - Propagation de la lumière
1. Sources et récepteurs de lumière
1.1. Sources lumineuses
On appelle source de lumière tout corps ou dispositif qui émet de la lumière.
Il existe deux types de sources de lumière :
$-\ $les sources lumineuses réelles ou primaires sont celles qui produisent la lumière qu'elles émettent.
Exemple :
Les sources primaires naturelles : le Soleil, les étoiles, les lucioles.
Les sources primaires artificielles : la bougie et les lampes allumées.
$-\ $les sources lumineuses apparentes ou secondaires celles qui renvoient la lumière qu'elles reçoivent d'autres sources lumineuses.
Exemples :
La lune, le miroir etc.
1.2. Récepteur de lumière
Un récepteur de lumière est un corps sensible à la lumière ou qui réagit à la lumière.
Exemples :
l'œil, la photorésistance, la peau, la chlorophylle$\ldots$
Il existe deux types de récepteurs de lumière :
$-\ $les récepteurs naturels.
Exemples :
l'œil, la chlorophylle, la peau$\ldots$
$-\ $les récepteurs artificiels.
Exemples :
la pellicule photographique, la photorésistance ou $LDR$, les photopiles ou pilessolaires, le chlorure d'argent$\ldots$
2. Propagation rectiligne de la lumière : notion de faisceau et rayon lumineux
2.1. Propagation rectiligne de la lumière
2.1.1. Expérience
Dans une salle obscure contenant de l'air, on place trois plaques en bois percé, entre une source de lumière
Exemple :
une lampe et l'œil d'un observateur.

2.1.2. Observation
La lumière de la bougie n'atteint l'œil d'un observateur que si les trous sont alignés, ce qui indique que la lumière se propage selon une ligne droite.
2.1.3. Conclusion
Dans un milieu de propagation transparent et homogène, la lumière se propage en ligne droite.
On parle de propagation rectiligne.
2.2. Rayon et faisceau lumineux
2.2.1. Rayon lumineux
On représente un rayon lumineux par une droite munie d'une flèche indiquant le sens de propagation.

2.2.2. Faisceau lumineux
On appelle faisceaux lumineux l'ensemble des rayons lumineux émis par une source primaire ou diffusés par une source secondaire
On distingue trois types de faisceaux lumineux :
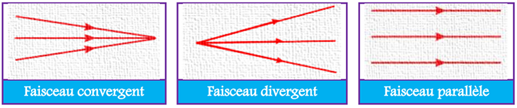
$\bullet\ $Les faisceaux cylindriques : tous les rayons sont parallèles.
$\bullet\ $Les faisceaux convergents : tous les rayons arrivent au même point.
$\bullet\ $Les faisceaux divergents : tous les rayons partent d'un même point
3. Vitesse de propagation de la lumière
3.1. Notion de la vitesse
On définit la vitesse comme étant le quotient de la distance parcourue par la durée :$$V=\dfrac{d}{t}$$
La vitesse de la lumière dans le vide, notée $c$, appelée célérité de la lumière est une constante universelle.
Sa valeur est : $c=299792458\,m\cdot s^{-1}$
C'est une vitesse limite.
On utilise généralement pour la vitesse de la lumière dans le vide et dans l'air la valeur voisine : $C=3\cdot 10^{8}m\cdot s^{-1}$
Remarque :
La distance $(d)$ parcourue par un faisceau de lumière, dans un intervalle de temps $(t)$ est donnée par la formule suivante :$$d=c\times t$$
3.2. Année lumière
Une année-lumière est une unité utilisée en astronomie pour exprimer les distances.
Elle correspond à la distance parcourue par la lumière dans le vide pendant une année : $1\text{al}=9.46\times 10^{12}km.$
C'est une unité de longueur notée : $\text{al}.$
II. Réflexion, réfraction, diffraction de la lumière
1. Réflexion et réfraction
1.1. La réflexion de la lumière
1.1.1. Observation
Lorsqu'une lumière provenant d'une source lumineuse tombe sur une surface plane et polie métallisée (miroir), une partie de cette lumière est renvoyée par la surface : c'est le phénomène de réflexion.
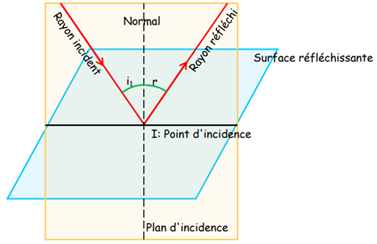
1.1.2. Définition
La réflexion de la lumière est le changement de direction de la lumière lorsqu'elle atteint la limite entre deux milieux et retourne dans le milieu d'origine.
Remarque :
L'écho est le phénomène de réflexion d'une onde sonore sur une surface ou sur des inhomogénéités existant dans le milieu de propagation ; l'onde ainsi réfléchie.
1.2. La réfraction de la lumière

Lorsqu'on envoie des rayons lumineux monochromatiques (Lasers) sur la surface libre de l'eau colorée avec de la fluorescéine, on constate que :
$-\ $Une petite partie de la lumière est réfléchie.
$-\ $Une majeure partie du faisceau pénètre dans l'eau avec un changement de direction : le faisceau semble brisé
Le premier phénomène est celui de la réflexion partielle.
Le phénomène pour lequel la lumière change de direction lorsqu'elle passe d'un milieu transparent à un autre, s'appelle la réfraction.
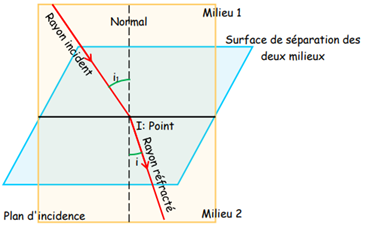
Quand un rayon lumineux incident arrive au niveau du point d'incidence $I$ avec un angle d'incidence $i_{1}$ le rayon traverse la surface de séparation entre les deux milieux et le rayon réfracté repart avec un angle de réfraction $i_{2}.$
1.3. Les lois de la réflexion et de réfraction de la lumière
Les phénomènes de réflexion et de réfraction sont régis par les lois de Snell-Descartes.
$1^{ère}$ loi :
Les rayons réfléchi et réfracté appartiennent au plan défini par le rayon incident et la normale à la surface de séparation (dioptre).
$2^{ème}$ loi :
Les angles d'incidence $i_{1}$ et de réflexion $r$ ont des valeurs identiques : $i_{1}=r$
$3^{ème}$ loi :
Les angles d'incidence $i_{1}$ et de réfraction $i_{2}$ sont liés par la relation : $n_{1}\cdot\sin\,i_{1}=n_{2}\cdot\sin\,i_{2}$ Où $n_{1}$ et $n_{2}$ sont des nombres sans unité appelés indices de réfraction, qui caractérisent les milieux d'incidence et de réfraction.
III. Interférences lumineuses
Deux ondes de même de fréquence se propageant dans le même milieu peuvent se superposer pour donner naissance aux phénomènes d'interférences.
Si la lumière est une onde, elle doit permettre d'obtenir un tel phénomène
1. Expérience des fentes de Young
1.1. Dispositif expérimental
Une source monochromatique intense éclaire un écran percé d'une fente $S.$
Cette fente donne naissance à un faisceau divergeant qui éclaire un second écran percé de deux fentes très fines et parallèles, $S_{1}$ et $S_{2}$, appelées fentes de Young.
Par le phénomène de diffraction, les deux fentes $S_{1}$ et $S_{2}$ se comportent comme des sources identiques divergentes.
Un écran, placé parallèlement au plan des fentes, recueille la lumière issue de $S_{1}$ et $S_{2}$
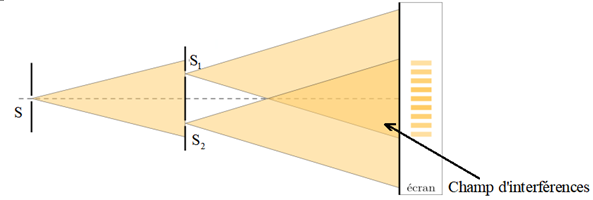
1.2. Observations
On observe sur l'écran des zones alternativement sombres et claires appelées franges d'interférence.
Ces franges au voisinage du point de projection $S$ sur l'écran sont pratiquement rectilignes, parallèles, équidistantes et perpendiculaires au plan de la figure.
Ces franges sont observées dans un champ d'interférence quelque soit la position de l'écran : on dit que ces franges sont délocalisées

1.3. Interprétation
L'existence des franges montre que sous certaines conditions la superposition de deux faisceaux lumineux peut :
$-\ $en certains points, accentuer le phénomène lumineux en donnant des franges brillantes
$-\ $en d'autres points, détruire le phénomène lumineux en donnant des franges sombres.
Le phénomène d'interférence peut s'interpréter si on suppose que les sources secondaires se comportent comme des sources de vibrations de même longueur d'onde.
En point $M$ de l'écran appartenant au champ d'interférence, les vibrations issues de $S_{1}$ et $S_{2}$ arrivent l'une par rapport l'autre avec un certain retard.
Il y a interférences constructives en un point de la zone d'interférences si la différence de marche en ce point est un multiple entier de la longueur d'onde : $\boxed{\delta=k\lambda\quad\left(k\in\mathbb{R}\right)}$
Le point $M$ est alors le milieu d'une frange brillante.
Il y a interférences destructives en un point de la zone d'interférences si la différence de marche en ce point est un multiple entier impair de la demi-longueur d'onde : $\boxed{\delta=\left(2k+1\right)\dfrac{\lambda}{2}\left(k\in\mathbb{R}\right)}$
Le point $M$ est alors le milieu d'une frange sombre
2. Conditions d'interférences
On ne peut obtenir d'interférences lumineuses avec des sources distinctes où on essaie de superposer les faisceaux.
Pour obtenir des franges d'interférences, il faut deux sources cohérentes
Deux sources sont cohérentes si :
$-\ $elles émettent des vibrations de même fréquence (même période).
On dit qu'elles sont synchrones
$-\ $elles présentent une différence de phase constante
$-\ $le rapport d'amplitude constant
3. Interfrange
3.1. Différence de marche
La différence de marche $(\text{notée }\delta)$ est la différence de distance parcourue par les deux ondes avant d'arriver au point $M$ $$\boxed{\delta=\dfrac{ax}{D}}$$
3.2. Position des franges
3.2.1. Position des milieux des franges brillantes
Les abscisses des milieux des franges brillantes sont tels que :$$\boxed{X_{k}=k\lambda\dfrac{D}{a}}$$
3.2.2. Position des milieux des franges sombres
Les abscisses des milieux des franges sombres sont tels que :$$\boxed{X_{k}=\left(2k+1\right)\dfrac{\lambda}{2}\dfrac{D}{a}}$$
3.3. Expression de l'interfrange

L'interfrange est la distance qui sépare deux franges consécutives de même nature $$\boxed{i=\lambda\dfrac{D}{a}}$$
Remarque :
L'ordre d'interférence en un point $M$ de l'écran où la différence de marche est $\delta$, est : $\boxed{p=\dfrac{\delta}{\lambda}}$ $\lambda$ étant la longueur d'onde de la radiation.
Si le point $M$ est le milieu d'une frange brillante, on a alors : $\boxed{p=\dfrac{\delta}{\lambda}=k}$
Les franges brillantes ont un ordre d'interférence entier.
Si le point $M$ est le milieu d'une frange sombre, on a alors : $\boxed{p=\dfrac{\delta}{\lambda}=k+\dfrac{1}{2}}$

Ajouter un commentaire