Bac physique chimie 2025 série F6

Une bobine joue plusieurs rôles importants dans differents domaines, principalement en électricité , en électronique et en électromagnétisme. 

Elle permet de produire un champ magnétique, un courant induit, des forces  électromagnétiques $\ldots$

On dispose d'une bobine longue ou solénoïde de rayon  $r=5\,cm$, comportant $N=1000$ spires jointives sur une seule couche et de longueur$\ell=80\,cm$ 

Il est parcouru par un courant d'intensité $I=20\,mA$

L'axe du  solénoïde est horizontal.
 
1.1 Faire un schéma vue de dessus sur lequel on fera apparaitre le sens du courant, les faces Nord et sud du solénoïde ainsi que le champ magnétique $\overrightarrow{B}_{S}$ créé par le courant  au centre $0$ du solénoïde.   

1.2. Calculer la valeur  du champ magnétique $B_{S}$ du solénoïde.                                                     

1.3. Quel doit être le diamètre $d$ et la  longueur $L$ du fil utilisé. 
          
1.4. L'axe du solénoïde est placé perpendiculairement au plan du méridien magnétique. 

Au centre $0$ du solénoïde on place une petite aiguille aimantée mobile sans frottement sur un pivot vertical. 

1.4.1. Quel est le champ magnétique responsable de l'orientation de l'aiguille pour $I=0$ ?             

1.4.2. Lorsque le courant d'intensité $I=20\,m\cdot A$ parcourt le solénoïde, l'aiguille tourne d'un angle de $57. 5^{\circ}$

En déduire l'intensité  de la composante horizontale  $\overrightarrow{B}_{h}$ du champ magnétique terrestre ainsi que celle du champ magnétique  $\overrightarrow{B}_{r}$  résultant au centre du solénoïde.                                                                      
 

 
Nous souhaitons déterminer les caractéristiques d'une bobine. 

Pour cela, on réalise le montage expérimental représenté à la figure $1$, comprenant :
 

 
$\bullet\ $une bobine $(b)$ d'inductance $L$ et de résistance $r$,
 
$\bullet\ $un conducteur ohmique $(D)$ de résistance $R$,
 
$\bullet\ $un générateur de tension $(G)$ de force électromotrice $E$,
 
$\bullet\ $Un interrupteur $K$

Dans une première expérience on mesure, à l'aide d'un ampèremètre, l'intensité  du courant en régime  permanent. 

On trouve $I=0.2A$
 
Dans une seconde expérience, on visualise, sur l'écran d'un oscilloscope bicourbe à mémoire, la tension $UR$ aux bornes du conducteur ohmique $(D)$ sur la voie $1$ et $U_{PQ}$ aux bornes du générateur sur la voie $2$ (courbes $1$ et $2$ de la figure $2$).

 
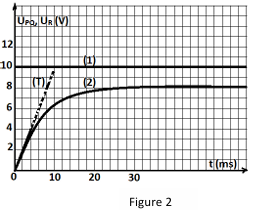
La droite $(T)$ représente la tangente à la courbe $2$ à la date $t=2$
 
2.1. Reproduire la figure $1$ en y indiquant les branchements de l'oscilloscope.      

2.2. Laquelle des courbes $1$ ou $2$ correspond à $U_{R}^$

calculer $R$
       
2.3. Laquelle des courbes $1$ ou $2$ permet de suivre l'évolution du courant dans le circuit. 

Justifier.               

2.4. Quel est le phénomène physique responsable de cette évolution de l'intensité du courant ?         

2.5. L'évolution du courant électrique peut être décrite par une équation différentielle. 

2.5.1.  Montrer que cette équation différentielle peut être écrite avec la tension $U_{R}$ aux bornes du conducteur ohmique et se mettre sous la forme : $L\dfrac{dU_{R}}{dt}+(R+r)U_{R}=ER$

2.5.2.  Que devient cette équation différentielle en régime permanent ? 

En déduire la valeur de $r$
      
     
2.5.3.  Définir la constante de temps $r$ du dipôle $Rl$ et détermine graphiquement sa valeur.    
         
2.5.4.   Montrer que $L=0.36\,H$

 
On étudie le comportement d'un condensateur de capacité $C$ dans un circuit série (figure 3).

     
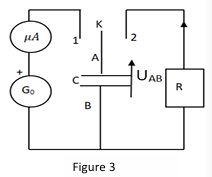
$Go$ est un générateur de courant idéal, $K$ est un Interrupteur qui permet de charger le condensateur $(K \text{en position }1)$ ou de le décharger $(K\text{ en position }2)$ à travers le conducteur ohmique de résistance $R=10\,k\Omega$

Un dispositif non représenté relève à intervalles de temps réguliers, la 
tension $U=_{Ab}=U_{0}$ aux bornes du condensateur. 

3.1. A la date $t=0$, le condensateur étant entièrement déchargé, on place $K$ en position $1$, le microampèremètre indique alors une valeur constante $I_{0}=10\,\mu A$ 

La figure $1$ représente les variations de la tension $U_{c}$ aux bornes du condensateur en fonction du temps.
 
3.1.1. Monter que la tension $U_{c}$ est donnée par la relation :  

$U_{c}=\dfrac{I_{0}}{C}t$

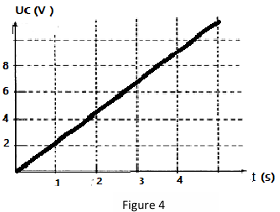
3.1.2. A l'aide de la figure $4$, déterminer la capacité $C$ du condensateur.                                       

3.2. Lorsque la tension aux bornes du condensateur est égale à $U_{6}+6\,V$, on bascule l'interrupteur $K$ en position $2$ à l'instant $t=0$
 
3.2.1. Montrer que la tension $U_{c}$  obéit à l'équation différentielle : 

$\dfrac{dU_{c}}{dt}+\dfrac{1}{RC}u_{C}+0$
         
3.2.2. Cette équation différentielle admet une solution de la forme : $U_{c}(t)=A\mathrm{e}^{-\dfrac{t}{t}}$ relation où $A$ et $t$ sont des constantes.

3.2.2.2. Calculer la valeur de $U_{c}$ à $t=5t$ 

Quelle remarque peut – on faire ? Donner la signification de $t$
 

 
Les systèmes de transfert de l'information tel que le téléphone, les radios et autres fonctionnent sur le principe de circuits oscillants en exploitant les phénomènes de résonance. 

On considère un circuit électrique oscillant et comportant un générateur, une bobine d'inductance $L$  et de résistance $R$ et un condensateur de capacité $C$ variable, montés en série. 

Le générateur impose entre ses bornes $A$ et $B$ une tension sinusoidale $U$ de fréquence $N=50\,Hz$