Bac sciences physiques 2025 serie S1-S1A-S3-S2-S2A8s4-S5

La glycine est un acide alpha aminé de formule :  

 
1.1. Donner son nom dans la nomenclature officielle.  

1.2. La glycine peut réagir avec un autre acide alpha aminé A pour donner un dipeptide de masse molaire $146/mol$

1.2.1. Déterminer $A$ et montrer que sa molécule est chirale. 

1.2.2. Donner les représentations de Fischer des $2$ énantiomères de $A$ 
 
Données : masses molaires atomiques en $g\cdot mol^{-1}M(C)=12$, $M(H)=1$, $M(O)=16.$

L'acide benzoïque $C_{6}H_{5}COOH$ pourra être noté $R-COOH(aq)$ en solution aqueuse dans la suite de l'exercice.
 
2.1. Écrire l'équation de la réaction entre l'acide benzoïque et l'eau. 

En déduire l'expression de la constante d'acidité $Ka$ du couple acide benzoïque / ion benzoate. 

2.2. Sachant que cette constante d'acidité vaut $6.3\cdot 10^{-5}$  à $25^{\circ}C$, calculer son $pKa$
 
Tracer le diagramme de prédominance du couple acide benzoïque / ion benzoate.
 
2.3. Le $pH$ d'une solution d'acide benzoïque vaut $6.0.$

Quelle est l'espèce prédominante dans cette solution ?
       

Un monoalcool saturé $A$ contient en masse $4.8$ fois plus de carbone que d'hydrogène. 

Son oxydation ménagée en milieu acide par le dichromate de potassium en défaut conduit à la formation d'un aldéhyde $B$ à chaîne carbonée ramifiée.  

3.1. Montrer que la formule brute de $A$ est $C_{4}H_{10}O$

3.2. Écrire les formules semi-développées de $A$ et $B$ et donner leur nom dans la nomenclature officielle. 
 
3.3. Écrire l'équation de la réaction d'oxydation de $A$ 
 
Données : couple  $Cr_{2}O_{7}^{2-}/Cr^{3+}$ ; 

masses molaires atomiques en $g\cdot mol^{-1}M(C)=12$, $M(H)=1$

Un point $M$ matériel décrit un cercle de rayon  $r=5\,cm$

Le point $M$ est repéré par son abscisse 

angulaire : $\theta=5t+\dfrac{\pi}{8}$avec $t$ (en seconde) et $\theta$ (en radian). 

4.1. Déterminer la vitesse angulaire, la fréquence et la période du mouvement. 

4.2. Quel est le module du vecteur vitesse linéaire de $M$ ? 

Quelle est la nature du mouvement ?  

4.3. Déterminer le vecteur accélération de $M$  
 

Un aimant droit crée en un point $P$ centre d'un solénoïde de $140$ spires et de longueur $16\,cm$ un champ magnétique de valeur $2.5\,mT$
 

 
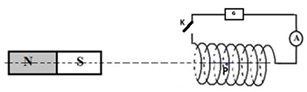
5.1. Représenter sur le schéma ci-dessus 

repris sur votre copie, le vecteur champ magnétique $\overrightarrow{B}_{\alpha}$
créé par l'aimant droit en $P$
 
5.2. Déterminer le sens et l'intensité du courant électrique fourni par le générateur $(G)$ qui va annuler le champ magnétique en $P$, lorsque l'interrupteur $K$ est fermé.
  
Donnée : perméabilité du vide $\mu_{0}=4\pi\cdot 10^{-7}SI.$

On considère un circuit électrique fermé comprenant un condensateur $AB$ de capacité $C=1\mu F$ et une bobine d'inductance $L$ de résistance négligeable.
       
La tension aux bornes du condensateur a pour expression $UAB=2\cos (5000\,t)$ 

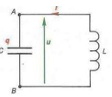
6.1. Calculer l'inductance $L$ de la bobine.
  
6.2. Établir successivement les expressions de la charge $q(t)$ portée par l'armature $A$ du condensateur et de l'intensité $i(t)$ du courant circulant dans le circuit.
  
6.3. Calculer l'énergie emmagasinée dans le circuit. 
 

Données : nombre d'Avogadro $N_{A}=6.02\cdot 10^{23}mol^{-1}$ ; masse molaire atomique de l'uranium $238$ $M=238\,g/mol$
 
On considère un échantillon d’'uranium $238\left(_{92}^{238}U\right)$ de masse$m=1\,g$ à un instant $t$ 

7.1. Calculer le nombre de noyaux d'uranium $238$ présent dans l'échantillon à l'instant $t.$

7.2. Sachant que l'activité de l'échantillon à l'instant $t$ vaut $A=12000\,Bq$, déterminer la constante radioactive de l'uranium $238.$

En déduire la demi-vie de cet isotope ? 

7.3. Combien de temps faut-il pour que $99\%$ d'une masse donnée de cet isotope se désintègre. 

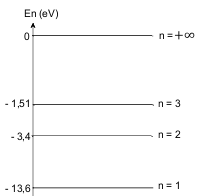
Une partie du diagramme énergétique de l'atome d'hydrogène est représentée ci-dessous. 
 
Données : constante de Planck $h=6.62\cdot 10^{-34}$ ; célérité de la lumière $c=3\cdot 10^{8}\,m\cdot s^{-1}$
 
8.1. Comment appelle-t-on les états correspondant respectivement à $n=1$ ; $n=2$ ; $n=+\inf$?  

8.2. Quelle est l'énergie minimale à fournir à un atome d'hydrogène pris à l'état fondamental pour 
l'ioniser. 

8.3. Calculer la longueur d'onde de la radiation correspondant à une transition du niveau 3 vers 
le niveau $2.$ 
 
$\begin{array}{|c|c|c|c|c|c|c|c|c|} \hline\text{Questions }&Q_{1}&Q_{2}&Q_{3}&Q_{4}&Q_{5}&Q_{6}&Q_{7}&Q_{8}\\ \hline S1-S3\text{(points)}&2&2&2&3&2&3&3&3\\ \hline S2-S4-S5\text{ (points)}&2.5&2.5&3&3&2.5&2.5&2&2\\ \hline \end{array}$