ENSA - Épreuve de Sciences Physiques - 2013
Exercice 1 : (7 points)
L'aspirine ou acide acétylsalicylique a pour formule semi-développée
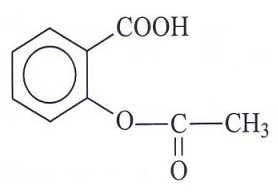
Sa masse molaire est M=180g/mol.
L'aspirine réagit à chaud sur la soude.
1) Nommer les fonctions oxygénées présentes dans la molécule. Encadrer ces fonctions.
2) L'action des ions OH− sur l'aspirine met en jeu deux types de réactions. Lesquelles ?
Préciser pour chaque réaction la fonction concernée.
Que peut-on dire de chacune des réactions du point de vue cinétique ?
3) Un comprimé d'aspirine dosé à 500mg est broyé puis mélange à 10mL de solution de soude molaire.
L'ensemble est chauffé pendant quelques minutes (réaction 1).
Après refroidissement ; on verse l'ensemble dans une fiole jaugé 200mL, on complète avec de l'eau distillée jusqu'au trait de jauge. On obtient une solution (S).
Pour déterminer l'excès d'ion d'hydroxyde, on dose 10mL de la solution (S) par une solution d'acide chlorhydrique de concentration 0.02mol/L.
L'équivalence est atteinte lorsqu'on a versé 10mL.
a) Écrire l'équation bilan de la réaction 1.
b) Calculer la quantité d'ions OH− initialement mélangée avec la comprimé d'aspirine.
c) Écrire l'équation bilan support du dosage qu'on notera réaction 2.
Calculer la quantité d'ions OH− dans la prise d'essai.
d) En déduire la quantité d'ions OH− consommée par la réaction 1 et la quantité d'acide acétylsalycilique
e) Calculer la masse d'acide acétylsalicylique présente dans un comprimé.
L'indication « aspirine dosée à 500mg » est elle exacte ?
Exercice 2 : (6 points)
On donne : g=9.8m/s2
Lors d'un match de football Barcelone-Real de Madrid, Messi tire un coup franc à 18.5m des buts, il communique à la balle une vitesse V0=57.6km/h faisant un angle α=30∘ avec la pelouse horizontale.
On considère la balle comme étant ponctuel et on néglige la résistance de l'air.
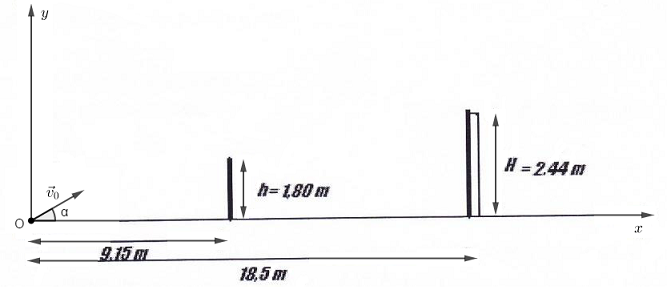
1) Établir les équations horaires du mouvement de la balle dans le repère (O, →i, →j) avec O point du tir (on supposera que le mouvement de la balle se fait dans le plan vertical (x, O, y).
En déduire l'équation de la trajectoire de la balle.
2) La balle est-elle interceptée par le mur de hauteur 1.80m situe à 9.15m de O ?
3) Le but est-il marqué sachant que le gardien n'a pas pu intercepter la balle ; la hauteur des camps étant de 2.44m
4) Quelle est la hauteur maximale atteinte par la balle ?
5) Quelle est la distance qui sépare le point de tir et le point de chute si aucun obstacle n'arrêtait la balle ?
Avec quelle vitesse la balle touche-t-elle le sol alors ?
Quels angles la vitesse devait-elle faire avec la pelouse pour que la balle heurte la barre transversale ?
Exercice 3 : (7 points)
Un faisceau de protons pénètre dans le champ électrique supposé uniforme existant entre les armatures horizontales d'un condensateur.
La d.d.p. entre l'armature supérieure A et l'armature inférieure B est U (U>0).
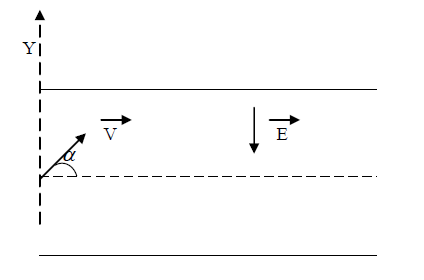
Les protons pénètrent dans le champ avec une vitesse V0 qui fait avec le champ électrique E, un angle de 135∘ (voir croquis).
On donne V0=2.105m/s; E=104V/m.
1) Écrire l'équation de la trajectoire des protons dans le champ électrique dans le système d'axes (O, →i, →j).
2) A quelle hauteur maximale les protons s'élèvent-ils au-dessus du point O ?
3) La longueur des armatures est L=5cm.
Déterminer les coordonnées du point S, point de sortie des protons du champ électrique.
4) Trouver la durée du trajet OS.
5) Déterminer les composantes du vecteur vitesse Vs des protons au moment où ils passent en S.
En déduire la norme du vecteur vitesse Vs et la déviation des protons.
On donne : Charge d'un proton q=1.6⋅10−19C
Masse du proton m=1.60⋅10−27kg
Durée 2 heures
Ajouter un commentaire