ENSA - Épreuve de Sciences Physiques - 2014

 

Répondre par $\text{VRAI}\ $ ou $\ \text{FAUX}$

 

1) L'acide $N_{2}N-CH_{2}-CH_{2}-COOH$ est un acide $\alpha$-aminé.

 

2) Les réactions suivantes sont des réactions acide-base :

 

a) $HCl\ +\ NaOH\ \longrightarrow\ NaCl\ +\ H_{2}O$

 

b) $H^{+}\ +\ H_{2}O\ \longrightarrow\ H_{3}O^{+}$

 

c) $NaOH\ \longrightarrow\ Na^{+}\ +\ OH^{-}$

 

d) $CH_{3}COO^{-}\ +\ H_{3}O^{+}\ =\ CH_{3}COOH\ +\ H_{2}O$

 

e) $HCl\ +\ H_{2}O\ \longrightarrow\ H_{3}O^{+}\ +\ Cl^{-}$

En $1898$, Félix Hoffman, chimiste allemand, réussit la synthèse de l'acide acétylsalicylique ou aspirine. 

 

Cette synthèse est réalisée à partir de l'acide salicylique et l'anhydride acétique ou anhydride éthanoïque. 

 

En effet, l'acide salicylique, comme l'acide acétylsalicylique, sont des antipyrétiques efficaces (médicaments contre la fièvre), mais le deuxième est moins agressif pour l'organisme que le premier.

 

 

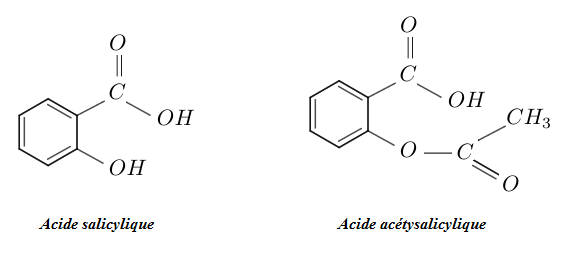
a) Expliquer simplement pourquoi ces deux corps peuvent présenter des activités pharmacologiques comparables. 

 

b) Nommer les différentes fonctions chimiques de l'acide salicylique et l'acide acétylsalicylique. 

 

c) Écrire l'équation-bilan de la réaction de synthèse de l'acide acétylsalicylique.

 

On donne : couple $H_{3}O^{+}/H_{2}O\ :\ K_{A}=1$ ; couple $H_{2}O/OH^{-}\ :\ K_{A}=10^{-14}.$ 

 

2) On étudie l'acide acétylsalicylique qui est un acide faible $(pK_{A}=3.48).$

 

a) Écrire l'équation-bilan de la réaction acido-basique de l'aspirine avec l'eau. 

 

Donner le nom de sa base conjuguée. Calculer la constante de réaction $K_{R}$ ; conclure. 

 

b) Le $pH$ est voisin de $1$ dans l'estomac et de $8$ dans l'intestin. 

 

Sous quelle forme prédominante se trouve l'aspirine dans chacun de ces organes ? 

 

Justifier la réponse

 

3) On prépare une solution $S$ de volume $150\;mL$ en dissolvant un comprimé d'aspirine dans l'eau distillée. 

 

On procède au dosage de la quantité d'acide acétylsalicylique contenu dans $S$ par une solution d'hydroxyde de sodium.

 

a) Le dosage est effectué à froid : expliquer pourquoi. 

 

b) Écrire l'équation-bilan de la réaction de dosage.

 

Calculer la constante de réaction $K_{R}$ ; conclure. 

 

c) La solution de soude utilisée a une concentration $C_{b}=0.15\;mol/L.$

 

Le volume versé à l'équivalence dans $S$ est $V_{b}=15.6\;mL.$

 

En déduire la masse d'aspirine contenue dans le comprimé.

Une petite bille de masse m décrit une gouttière de forme circulaire $ABCD$ d'épaisseur négligeable de rayon $r$ et de masse $M$, situé dans un plan vertical. 

 

Soit $OK$ la ligne de plus grande pente d'un plan incliné faisant l'angle $\theta$ avec l'horizontale passant par $O\ $ et $\ A.$

 

On note $Ox\ $ et $\ Oy$ les deux axes orthonormés passant par $A\ $ et $\ B$ (voir figure. Ce repère ne sera utilisé que pour la dernière question). On néglige tous les frottements.

 

 

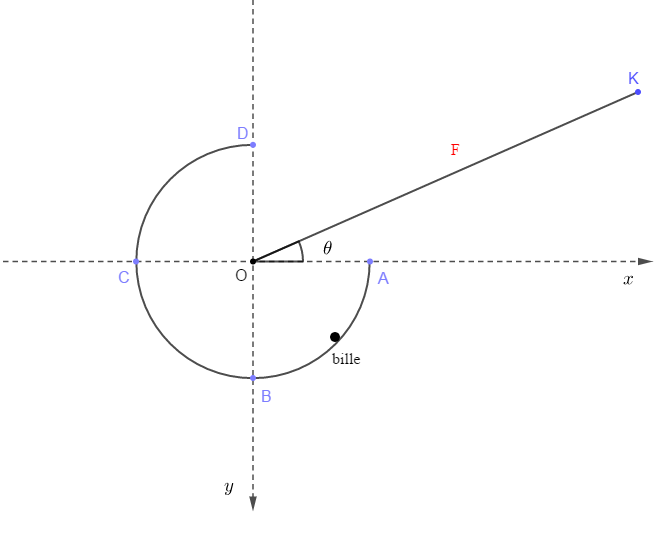
Soit $\vec{R}$ la réaction de la gouttière sur la bille. On pose $\alpha= (\vec{R}\;,\ \vec{P})$, l'angle que font entre eux la réaction $\vec{R}$ et le poids $\vec{P}$ de la bille $(0\leq \alpha\leq \pi).$

 

1) Si $\vec{v}$ est la vitesse de la bille en un point quelconque de la gouttière, montrer que le module de $\vec{R}$ peut se mettre sous la forme $R=m\left(\dfrac{v^{2}}{r}-g\cos\alpha\right).$

 

2) La bille partant du point $A$ à l'instant initial, exprimer la vitesse $v$ à l'instant quelconque $t$ en fonction du rayon $r$, de l'angle $\alpha$ et de la vitesse $v_{A}$ au point $A.$

 

Déduire l'expression de $R$ en fonction $v_{A}\;,\ r\ $ et $\ \alpha.$ 

 

3) Soit $E$ le point milieu l'arc $CD.$

 

a) Quelle doit être la valeur minimale de $v_{A}$ pour que la bille $m$ ne décolle pas de la gouttière au point $E\ ?$

 

b) Même question concernant le point $D.$

 

Calculer alors les coordonnées de $F$, point d'arrivée de le bille sur $OK.$

 

On donne : $r=50\;cm\;;\ g=9.81\;m.s^{-1}\;;\ \theta=30^{\circ}.$ 

A) Un condensateur de capacité $C=3\;\mu F$ est chargé à l'aide d'un générateur de tension de force électromotrice $U=10\;V.$

 

Quelle est la charge $Q_{0}$ du condensateur à la fin de cette opération et quelle est l'énergie emmagasinée par le condensateur ?

 

B) Le condensateur chargé est déconnecté du générateur et ses armatures sont reliées aux bornes d'une bobine $(L=120\;mH\ $ et $\ r=0$ dans cette question). 

 

On observe ce qui se passe à l'aide d'un oscilloscope. 

 

Faire le schéma du montage en indiquant les branchements de l'oscilloscope.

 

Quelle grandeur physique suit-on sur l'écran ? 

 

Donner l'aspect de la figure observée ?

 

C) Donner une interprétation énergétique du phénomène.

 

D. Établir l'équation différentielle vérifiée par la tension $u(t)$ aux bornes du condensateur.

 

E) Le condensateur chargé est relié à la bobine à un instant pris comme origine des dates.

 

1) Calculer la période $T_{0}$ des oscillations.

 

2) Déterminer l'expression de la charge $Q(t).$

 

3) Calculer la valeur maximale de l'intensité

 

$$\text{Durée 2 heures}$$