ESP - Epreuve de Physique - 2013
Problème 1 (4 points)
Pour mesurer l'indice $n$ d'un milieu solide transparent, on baigne la première face d'un prisme d'angle au sommet $A=90^{\circ}$ dans un milieu d'indice $n$ tandis que la seconde face est dans l'air.
On envoie un pinceau de lumière monochromatique sous incidence rasante sur la première face du prisme, et l'on mesure son angle d'émergence $i'$ dans l'air. On trouve $i'=60^{\circ}.$
Connaissant l'indice $N=\sqrt{3}$ du prisme, déterminer $n.$
Les incertitudes sur $N\ $ et $\ i'$ étant respectivement $\Delta N=10^{-5}\ $ et $\ \Delta i'=1'$, déterminer l'incertitude sur $n.$
$N$ pouvait-il être choisi quelconque ?
Problème 2 (4 points)
Une sphère $(S)$ de rayon $R$ porte une densité surfacique de charges $\sigma(\theta)=\sigma_{0}\cos\theta$ à symétrie de révolution autour d'un axe diamétral $Ox$ (voir figure). On demande de calculer le champ électrique aux points $O\;,\ A\ $ et $\ A'$ de l'axe $Ox.$
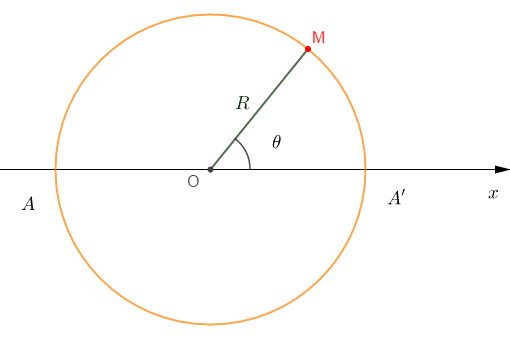
Problème 3 (6 points)
On étudie les transformations quasi statiques d'un gaz parfait (caractérisé par $\gamma=\dfrac{C_{p}}{C_{v}}=\text{constante})$ pour lesquelles la pression $P$ et le volume $V$ vérifient :
$$PV^{\alpha}=\text{constante}\quad(\alpha\neq 1)$$
1) Calculer le travail $W$ et l'énergie thermique $Q$ reçus par le gaz dans une transformation mécaniquement réversible, depuis l'état $(P_{1}\;,\ V_{1})$ jusqu'à l'état $(P_{1}\;,\ V_{1}).$
Exprimer le rapport $\dfrac{Q}{W}$ en fonction seulement de $\alpha\ $ et $\ \gamma.$
2) a) Pour quelle valeur de $\alpha$ la transformation envisagée ici est-elle adiabatique ?
b) Plus généralement, on définit la capacité thermique molaire $C(\alpha)$ selon :
$$Q_{\text{mol}}=C(\alpha)\Delta T$$
Exprimer $C(\alpha)$ en fonction de $C_{v}\;,\ \alpha\ $ et $\ \gamma$
Problème 4 (6 points)
Soit une particule de masse $m$ et de charge $q.$
A l'instant $t=0$, elle est lâchée sans vitesse initiale dans une région de l'espace où règne un champ magnétique uniforme $B$ parallèle à l'axe $Oz$ et un champ électrique uniforme $E$ parallèle à l'axe $Oy.$
Déterminer le mouvement de la particule.
$$\text{Durée 3 heures}$$

Ajouter un commentaire