Vous êtes ici

Notion d'acide fort et de base forte : Réaction entre acide fort et base forte - Ts

Classe:

Terminale

I. Acide fort

1. Étude d'un exemple : le chlorure d'hydrogène

1.1 Étude qualitative

Le chlorure d'hydrogène

$HCl$ , à la température ordinaire, est un gaz très soluble dans l'eau.

Les solutions obtenues par mise en solution du chlorure d'hydrogène dans l'eau portent le nom de solutions d'acide chlorhydrique

Une solution d'acide chlorhydrique conduit le courant électrique et subit l'électrolyse ; elle contient donc des porteurs de charge c'est-à-dire des ions

La présence des ions

$Cl^{-}$ se caractérise par la formation d'un précipité blanc de chlorure d'argent

$AgCl$ quand on ajoute quelques gouttes d'une solution de nitrate d'argent

La mise en évidence d'ions hydroduim

$H_{3}O^{+}$ s'effectue au moyen d'un indicateur coloré : l'hélianthine

Quand on verse quelques gouttes d'acide chlorhydrique dans de l'eau distillée additionnée de quelques gouttes d'hélianthine, une couleur rouge apparait

Les solutions d'acide chlorhydrique sont très corrosives ; la dilution des solutions concentrées est très exothermique et s'accompagner de projections.

1.2 Étude quantitative

A partir d'une solution commerciale de chlorure hydrogène, on réalise, par dilution, une solution de concentration

$C=10^{-2}mol\cdot L^{-1}$

La mesure du

$pH$ de la solution diluée à l'aide d'un

$pH-$ mètre donne la valeur égale

$2$

Montrons que l'acide chlorhydrique est un acide fort

Les espèces chimiques présentes dans la solution :

$-\$ les ions hydronium

$H_{3}O^{+}$ provenant de l'autoprotolyse de l'eau et du chlorure d'hydrogène

$HCl$

$-\$ des ions

$Cl^{-}$ provenant de l'action de l'eau sur le chlorure d'hydrogène

$-\$ des ions

$OH^{-}$ provenant de l'autoprotolyse de l'eau

$-\$ et éventuellement des molécules de chlorure d'hydrogène

$HCl$ non ionisées

$pH=2\Rightarrow\left[H_{3}O^{+}\right]=10^{-2}mol\cdot L^{-1}$

Le produit ionique s'écrit :

$\begin{array}{lcl} Ke&=&\left[H_{3}O^{+}\right]\left[OH^{-}\right]\\&\Rightarrow&\left[OH^{-}\right]=\dfrac{Ke}{\left[H_{3}O^{+}\right]}\\&=&\dfrac{10^{-14}}{10^{-2}}\\&\Rightarrow&\left[OH^{-}\right]=10^{-12}mol\cdot L^{-1} \end{array}$

L'électroneutralité de la solution s'écrit :

$\begin{array}{lcl} \left[H_{3}O^{+}\right]&=&\left[OH^{-}\right]+\left[Cl^{-}\right]\\&\Rightarrow&\left[Cl^{-}\right]=\left[H_{3}O^{+}\right]-\left[OH^{-}\right]\\&=&10^{-2}-10^{-12}\\&\Rightarrow&\left[Cl^{-}\right]=10^{-2}mol\cdot L^{-1} \end{array}$

La conservation de la matière s'écrit :

$\begin{array}{lcl} \left[HCl\right]_{i}&=&\left[HCl\right]_{d}+\left[HCl\right]_{r}\\&\Rightarrow&\left[HCl\right]_{r}=\left[HCl\right]_{i}-\left[HCl\right]_{d}\\&=&C-\left[Cl^{-}\right]\\&=&10^{-2}-10^{-2}\\&\Rightarrow&\left[HCl\right]_{r}=0\,mol\cdot L^{-1} \end{array}$

Les molécules de chlorure d'hydrogène

$HCl$ n'existent pratiquement pas en solution

La réaction entre le chlorure d'hydrogène

$HCl$ et l'eau est donc totale et l'on écrit :

$HCl\ +\ H_{2}O\ \rightarrow\ H_{3}O^{+}\ +\ Cl^{-}$

La réaction entre le chlorure d'hydrogène

$HCl$ et l'eau étant totale, on dit que

$HCl$ est un acide fort

2. Solutions aqueuses d'acides forts

2.1 Définition

Un acide fort est une espèce chimique qui s'ionise totalement dans l'eau pour donner des ions hydronium

$H_{3}O^{+}$

2.2 Exemples d'acides forts

$HCl$ : acide chlorhydrique ;

$HBr$ : acide bromhydrique ;

$HI$ : acide iodhydrique ;

$HNO_{3}$ : acide nitrique ;

$HClO_{4}$ : acide perchlorique ;

$H_{2}SO_{4}$ : acide sulfurique (diacide)

2.3 $pH$ d'une solution d'acide fort

Soit une solution aqueuse de monoacide fort

$AH$ de concentration molaire

$C$

L'action de l'eau sur l'acide est une réaction totale qui se traduit par l'équation-bilan :

$AH\ +\ H_{2}O\ \rightarrow\ H_{3}O^{+}\ +\ A^{-}$

$\left[H_{3}O^{+}\right]=pH$

$\Rightarrow pH=-\log\left[H_{3}O^{+}\right]$

$\Rightarrow pH=-\log\,C$

Pour une solution d'un diacide fort, l'équation-bilan s'écrit :

$AH_{2}\ +\ 2H_{2}O\ \rightarrow \ 2H_{3}O^{+}\ +\ A^{2-}$

$\left[H_{3}O^{+}\right]=2C$

$\Rightarrow pH=-\log\left[H_{3}O^{+}\right]$

$\Rightarrow pH=-\log\,2C$

Remarque :

Pour des concentrations molaires volumiques

$C$ telles que

$10^{-6}mol\cdot L^{-1}<C<10^{-1}mol\cdot L^{-1}$ , c'est la réaction :

$AH\ +\ H_{2}O\ \rightarrow \ H_{3}O^{+}\ +\ A^{-}$ qui est prépondérante

Pour des concentrations

$C>10^{-6}mol\cdot L^{-1}$ , c'est la réaction d'autoprotolyse de l'eau

$\left(2H_{2}O\ \rightarrow\ H_{3}O^{+}\ +\ OH^{-}\right)$ qui est prépondérante

Quand on dilue à l'infini une solution acide le

$pH$ tend vers

$7$

II. Base forte

1. Étude d'un exemple : l'hydroxyde de sodium $NaOH$

1.1 Étude qualitative

L'hydroxyde de sodium ou soude est un solide blanc de formule

$NaOH.$

C'est un solide ionique, constitué d'ions sodium

$Na^{+}$ et d'ions hydroxyde

$OH^{-}$ dont la mise en solution est fortement exothermique

La présence des ions sodium

$Na^{+}$ est mise en évidence par le test à la flamme.

La couleur jaune orange de la flamme révèle la présence de l'élément sodium

La mise en évidence des ions

$OH^{-}$ s'effectue au moyen d'un indicateur coloré : la phénolphtaléine, une coloration rouge violacée apparait

La couleur rouge violacé de la phénolphtaléine caractérise une solution contenant des ions hydroxyde

$OH^{-}$

L'hydroxyde de sodium est un produit très corrosif.

Sa dissociation et la dilution de ses solutions concentrées sont très exothermiques et peuvent s'accompagner de projections

1.2 Étude quantitative

On dissout

$0.4\,g$ d'hydroxyde de sodium dans un

$1\,L$ d'eau.

La solution ainsi préparée a une concentration en

$NaOH$

$C=10^{-2}mol\cdot L^{-1}$

La mesure du

$pH$ de la solution à l'aide du

$pH-$ mètre donne une valeur égale

$12$

Montrons que la dissociation de l'hydroxyde de sodium

$NaOH$ dans l'eau est totale

Les espèces chimiques présentes dans la solution sont :

$Na^{+}$ ,

$OH$ ,

$H_{3}O^{+}$ et éventuellement

$NaOH$ non dissociée

$pH=12$

$\Rightarrow\left[H_{3}O^{+}\right]=10^{-12}$

$\Rightarrow\left[H_{3}O^{+}\right]=10^{-12}mol\cdot L^{-1}$

Le produit ionique de l'eau s'écrit :

$\begin{array}{lcl} Ke&=&\left[H_{3}O^{+}\right]\left[OH^{-}\right]\\&\Rightarrow&\left[OH^{-}\right]=\dfrac{Ke}{\left[H_{3}O^{+}\right]}\\&=&\dfrac{10^{-14}}{10^{-12}}\\&\Rightarrow&\left[OH^{-}\right]=10^{-2}mol\cdot L^{-1} \end{array}$

L'électroneutralité de la solution s'écrit :

$\begin{array}{lcl} \left[H_{3}O^{+}\right]+\left[Na^{+}\right]&=&\left[OH^{-}\right]\\&\Rightarrow&\left[Na^{+}\right]=\left[OH^{-}\right]-\left[H_{3}O^{+}\right]\\&=&10^{-2}-10^{-12}\\&\Rightarrow&\left[Na^{+}\right]=10^{-2}mol\cdot L^{-1} \end{array}$

La conservation de la matière s'écrit :

$\begin{array}{lcl} \left[NaOHC\right]_{i}&=&\left[NaOHC\right]_{d}+\left[NaOHC\right]_{r}\\&\Rightarrow&\left[NaOHC\right]_{r}=\left[NaOHC\right]_{i}-\left[NaOHC\right]_{d}\\&=&C-\left[Cl^{-}\right]\\&=&\dfrac{0.4}{40\times 1}-10^{-2}\\&\Rightarrow&\left[NaOHC\right]_{r}=0\,mol\cdot L^{-1} \end{array}$

Les molécules d'hydroxyde de sodium

$NaOH$ n'existent pratiquement pas en solution

La réaction entre l'hydroxyde de sodium

$NaOH$ et l'eau est donc totale et l'on écrit :

$NaOH\stackrel{H_{2}O}{\longrightarrow}\ Na^{+}\ +\ OH^{-}$

La réaction entre l'hydroxyde de sodium

$NaOH$ et l'eau étant totale, on dit que

$NaOH$ est une base forte

2. Solutions aqueuses de bases fortes

2.1 Définition

Une base forte est une espèce chimique qui s'ionise totalement dans l'eau pour donner des ions hydroxyde

$OH^{-}$

2.2 Exemples de bases fortes

$NaOH$ : hydroxyde de sodium ;

$KOH$ : hydroxyde de potassium ;

$Ca\left(OH\right)_{2}$ : hydroxyde de calcium (dibase) ;

$C_{2}H_{5}O^{-}$ : ion éthanoate

2.3

$pH$ d'une solution de base forte

Soit une solution aqueuse de monobase forte

$BOH$ de concentration molaire

$C$

L'action de l'eau sur la base est une réaction totale qui se traduit par l'équation-bilan :

$BOH\stackrel{H_{2}O}{\longrightarrow}\ OH^{-}\ +\ B^{+}$

$\begin{array}{lcl} \left[OH^{-}\right]&=&C\\&\Rightarrow& pH=-\log\left[H_{3}O^{+}\right]\\&=&-\log\dfrac{Ke}{\left[OH^{-}\right]}\\&=&-\log\dfrac{10^{-14}}{C}\\&\Rightarrow&pH=14+\log\,C \end{array}$

Pour une solution d'une dibase forte, l'équation-bilan s'écrit :

$B\left(OH\right)_{2}\stackrel{H_{2}O}{\longrightarrow}\ B^{2+}\ +\ 2OH^{-}$

$\left[OH^{-}\right]=2C\ \Rightarrow\;pH=14+\log\,2C$

Remarque :

Pour des concentrations molaires volumiques

$C$ telles que

$10^{-6}mol\cdot L^{-1}<C<10^{-1}mol\cdot L^{-1}$ , c'est la réaction :

$BOH\stackrel{H_{2}O}{\longrightarrow}\ OH^{-}\ +\ B^{+}$ qui est prépondérante

Pour des concentrations

$C<10^{-6}mol\cdot L^{-1}$ , c'est la réaction d'autoprotolyse de l'eau

$\left(2H_{2}O\right)\ \longrightarrow\ H_{3}O^{+}\ +OH^{-}$ qui est prépondérante

Quand on dilue à l'infini une solution basique le

$pH$ tend vers

$7$

III. Réaction entre acide fort et une base forte

1. Étude qualitative

Quand on mélange une solution d'acide chlorhydrique

$HCl$ et un base

$NaOH$ , on constate :

$-\$ une élévation de la température du milieu réactionnel : on dit que la réaction est exothermique

$-\$ une variation du

$pH$ du milieu

$-\$ une variation des quantités de matière des ions hydronium

$H_{3}O^{+}$ et des ions hydroxyde

$OH^{-}.$

Ce qui nous permet de conclure qu'il y a une réaction acide-base

L'équation-bilan de la réaction s'écrit :

$H_{3}O^{+}\ +\ OH^{-}\ \rightarrow\ 2H_{2}O$

Cette réaction est la réaction inverse de l'autoprotolyse de l'eau ; elle est donc totale.

Les ions

$Na^{+}$ et

$Cl^{-}$ n'interviennent pas dans la réaction : ce sont des ions spectateurs

2. Étude quantitative

2.1 Variation du $pH$ au cours de la réaction

2.1.1 Étude expérimentale

A l'aide d'une pipette jaugée, on place dans un bécher

Un volume

$V_{A}$ d'acide chlorhydrique de concentration

$C_{A}$ inconnue à déterminer

Puis à l'aide d'une burette graduée placée au-dessus du bécher, on verse petit à petit dans le bécher la solution d'hydroxyde de sodium de concentration

$C_{B}$ connue (voir schéma du montage ci-dessous)

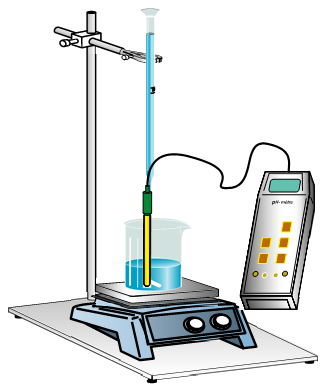
L'agitateur magnétique permet d'homogénéiser le mélange après ajout de la solution d'hydroxyde de sodium

Pour différentes valeurs de

$V_{B}$ de soude ajouté, on mesure le

$pH$ de la solution obtenue à l'aide

$pH-$ mètre préalablement étalonné

On obtient la courbe

$pH=f(V_{B})$ suivante :

2.1.2 Étude la courbe

La courbe

$pH=f(V_{B})$ est croissante : elle présente deux parties distinctes

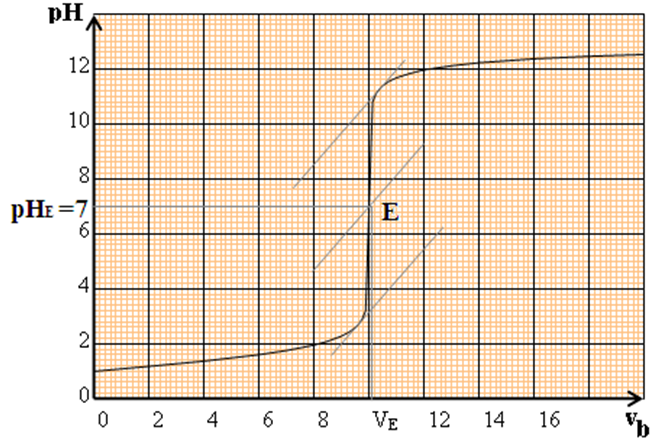
$-\$ Pour

$V_{B}\leq 8\,mL$ , la courbe est presque rectiligne et le

$pH$ varie peu lors de l'addition de la solution d'hydroxyde de sodium

$-\$ Pour

$8\,mL\leq V_{B}\leq 12\,mL$ , nous observons un

$«$ saut de

$pH »$ et la courbe change de concavité

$-\$ Pour

$V_{B}\geq 12\,mL$ ,

$pH$ varie peu

Ensuite faiblement, la courbe

Tendant vers une asymptote horizontale

Pour

$V_{B}=9.8\,mL$ , la courbe change de concavité : il existe donc un point d'inflexion dans cette partie de la courbe

Étudions les propriétés de la solution en ce point, noté

$E$

2.2 Point d'équivalence

2.2.1 Définition

Il y a équivalence lorsque les réactifs ont été mélangés dans les proportions stœchiométriques de la réaction de dosage

La réaction étudiée ici a pour équation :

$H_{3}O^{+}\ +\ OH^{-}\ \rightarrow\ 2H_{2}O$

A l'équivalence :

$n_{H_{3}O^{+}}=n_{OH^{-}}\Rightarrow\ C_{A}V_{A}=C_{B}V_{BE}$

2.2.2 Détermination du point d'équivalence

Le point d'équivalence

$E$ est le point de la courbe telque

$V_{B}=V_{BE}$

Le point d'inflexion de la courbe correspond au point d'équivalence, ceci permet de déterminer la position de

$E$ par la méthode des tangentes

$\bullet\$ Méthode des tangentes

$-\$ On trace tout d'abord deux tangentes à la courbe parallèles et situées de part et d'autre du point d'équivalent

$-\$ On trace une parallèle à ces deux tangentes équidistantes de celles-ci.

Son intersection avec la courbe

$pH=f(V_{B})$ détermine le point d'équivalent

$E$

$\bullet\$ Autre méthode : emploi des indicateurs colorés

Un indicateur coloré convient pour le dosage acido-basique si sa zone de virage contient le

$pH$ du point d'équivalence

$(pH_{E}=7)$

$B.B.T$

$($ zone de virage :

$6.1-7.6)$ est le plus approprié

Mais étant donné l'amplitude de la variation du

$pH$ , l'hélianthine

$(3.1-4.4)$ ou la phénolphtaléine convient également dès lors que les solutions intervenant dans le dosage ne sont très diluées

IV. Applications aux dosages

Les analyses constituent de nos jours une part importante de l'activité expérimentale des entreprises de chimie de synthèse, des organismes de contrôle ou des laboratoires de recherche : qu'elles soient bactériologiques, sanguines, d'urines, organiques ou minérales, les analyses reposent sur une technique appelée dosage.

Mais les méthodes utilisées dépendent de la quantité et des propriétés de l'espèce à analyser, mais aussi de la précision souhaitée

1. Principe d'un dosage acido-basique

Doser une espèce chimique dans une solution consiste à déterminer la quantité de matière ou la concentration molaire inconnue de l'espèce en solution.

Pour cela, on réalise une réaction acidobasique qui doit impérativement être :

$\bullet\$ unique : l'espèce titrante ne doit pas réagir avec d'autres espèces que l'espèce à titrer, et ne doit pas donner d'autres produits que ceux de la réaction de titrage, sinon la mesure du volume versé n'est pas fiable

$\bullet\$ totale : chaque goutte de l'espèce titrante doit réagir intégralement avec l'espèce à titrer, sinon la mesure du volume versé n'est pas fiable

$\bullet\$ et rapide : on ne doit pas être obligé d'attendre plusieurs minutes ou plusieurs heures après chaque ajout de l'espèce titrante

La relation entre les concentrations des solutions acide et basique à l'équivalence permet de calculer la concentration inconnue.

Il existe deux moyens pour déterminer l'équivalence : le dosage colorimétrique et le dosage

$pH-$ métrique

2. Dosage $pH-$ métrique

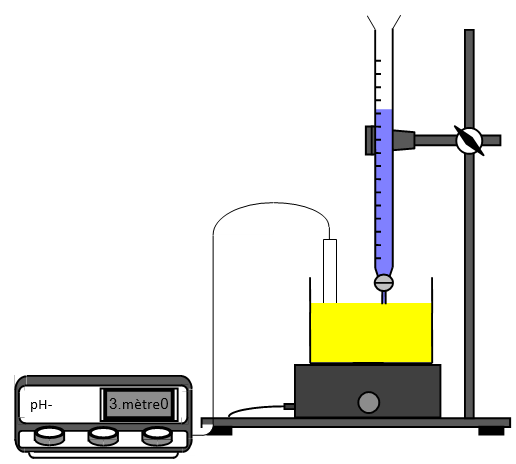
Pour doser une solution acide, par exemple, on utilise le montage ci-dessus.

On place cette solution dans le bécher

$($ volume

$V_{A}$ connu ; concentration

$C_{A}$ à déterminer

$)$ en ajoutant, si nécessaire, de l'eau distillée, pour que les électrodes trempent correctement

$($ cet ajout ne modifie pas la quantité d'ions

$H_{3}O^{+})$ et la solution d'hydroxyde de sodium

$($ concentration

$C_{B}$ connue

$)$ dans la burette graduée.

On note les valeurs de

$pH$ correspondant à l'ajout du volume

$V_{B}$ de solution d'hydroxyde de sodium

On trace la courbe représentant

$pH=f(V_{B})$ sur papier millimétré, on détermine le point d'équivalence

$E$ soit en considérant qu'il correspond à

$pH=7$ , soit en utilisant la méthode des tangentes parallèles et on calcule la concentration

3. Dosage colorimétrique

Les indicateurs colorés sont des substances dont la couleur dépend du

$pH$ ; leur changement de couleur se produit dans un domaine de

$pH$ relativement étroit que l'on appelle zone de virage

Tableau présentant les trois principaux indicateurs colorés usuels avec leur zone de virage

$\begin{array}{|c|c|c|c|} \hline \text{Indicateur coloré}&\text{Couleur acide}&\text{zone de virage}&\text{Couleur basique}\\ \hline \text{Hélianthine}&\text{rouge}&3.1-4.4&\text{jaune}\\ \hline \text{Bleu de bromothymol}&\text{jaune}&6.0-7.6&\text{bleu}\\ \hline \text{Phénolphtaléine}&\text{incolore}&8.2-10.0&\text{rose}\\ \hline \end{array}$

Dans un dosage colorimétrique, il faut choisir un indicateur coloré dont la zone de virage contient le

$pH$ du point d'équivalence.

Dans le cas d'un dosage acide fort - base forte, le

$pH$ du point d'équivalence est égal à

$7.0$ et le bleu de bromothymol

$($ zone de virage

$6.0-7.6)$ est un indicateur qui convient dans tous les cas, que les solutions soient concentrées ou diluées

4. Application : dosage d'une base forte par un acide fort

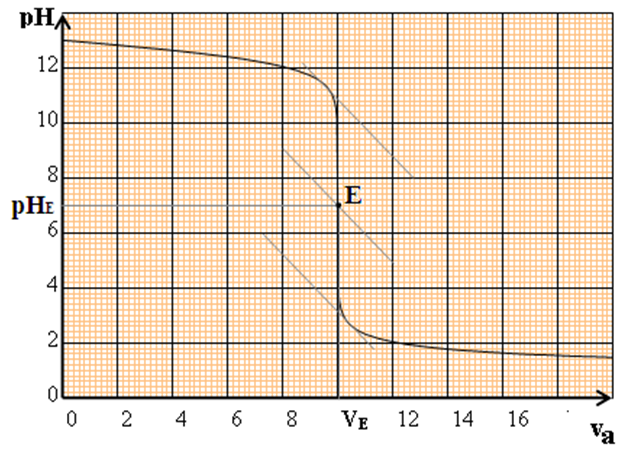
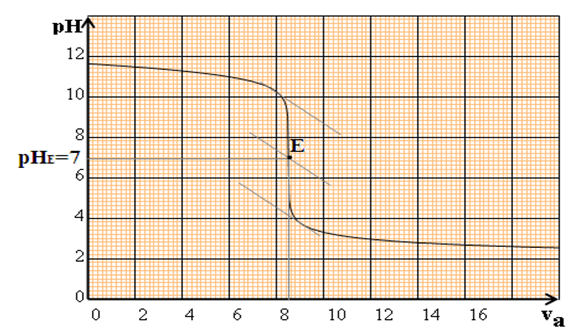
La courbe

$pH$ en fonction de

$V_{B}$ est décroissante : elle comporte trois parties distinctes :

$-\$ pour

$V_{a}\leq 8\,mL$ , la courbe est presque rectiligne et le

$pH$ varie peu lors de l'addition de l'acide fort

$-\$ pour

$8\,mL\leq V_{a}\leq 12\,mL$ , on observe un

$«$ saut de

$pH$

$»$ et la courbe change de concavité-pour

$V_{a}\geq 12\,mL$ , le

$pH$ varie ensuite faiblement, la courbe tendant vers une asymptote horizontale

Dans cette zone ou la concavité de la courbe s'inverse, le

$pH$ varie beaucoup et on y trouve le point équivalent

$E.$

La connaissance de

$E$ va permettre de calculer la concentration

$C_{a}$ inconnue

Exercice d'application

D'après le graphe représentant la variation du

$pH$ en fonction du volume d'acide versé :

Il faut verser

$8.5\,mL$ d'une solution d'acide chlorhydrique de concentration molaire

$10^{-2}mol\cdot L^{-1}$ dans

$20\,mL$ d'une solution d'hydroxyde de sodium pour obtenir l'équivalence acido-basique.

1) Quel est le

$pH$ à l'équivalence ?

2) Calculer la concentration molaire de la solution basique.

Quel est le

$pH$ de la solution basique ?

3) Vers quelle valeur tend le

$pH$ de la solution lorsqu'on continue à ajouter la solution acide ?

4) En utilisant les résultats précédents, tracer le graphe représentant la variation du

$pH.$

5) Calculer la concentration molaire des ions spectateurs

$Na^{+}$ et

$Cl^{-}$ présents dans le bécher à l'équivalence... ainsi que celles des ions

$H_{3}O^{+}$ et

$OH^{-}.$

En déduire la masse de chlorure de sodium

$NaCl$ dissoute à l'équivalence.

Cette masse augmente-t-elle après l'équivalence ?

Solution

1) Le

$pH$ à l'équivalence est égale

$7$

2) Calcul de la concentration molaire de la solution basique

A l'équivalence :

$\begin{array}{lcl} C_{B}V_{B}&=&C_{A}V_{A}\\&\Rightarrow&C_{B}=\dfrac{C_{A}V_{A}}{V_{B}}\\&=&\dfrac{1\cdot 10^{-2}\times 8.5}{20}\\&\Rightarrow&C_{B}=4.25\cdot 10^{-3}mol\cdot L^{-1} \end{array}$

3) Valeur vers laquelle tend le

$pH$ de la solution lorsqu'on continue à ajouter la solution acide

Lorsqu'on continue à ajouter la solution acide

$n_{A}>n_{B}$ ; la solution est donc acide

$\Rightarrow\ pH=-\log\,C_{A}\text{ avec }C_{A}=\dfrac{C_{A}V_{A}}{V_{A}+V_{B}}$

$\Rightarrow\ pH=-\log\dfrac{C_{A}V_{A}}{V_{A}+V_{B}}=-\log\dfrac{V_{A}C_{A}}{V_{A}\left(1+\dfrac{V_{B}}{V_{A}}\right)}$

$\Rightarrow\ pH=-\log\,C_{A}\text{ car }\dfrac{V_{B}}{V_{A}}\rightarrow\;0$

$\Rightarrow\ pH=-\log\;1\cdot 10^{-2}\ \Rightarrow\;pH=2$

4) Tracé du graphe représentant la variation du

$pH$

5) Calcul de la concentration molaire des ions spectateurs

$Na^{+}$ et

$Cl^{-}$ et des ions

$H_{3}O^{+}$ et

$OH^{-}$ à l'équivalence

$\begin{array}{lcl} \left[Cl^{-}\right]&=&\dfrac{C_{A}V_{A}}{V_{A}+V_{B}}\\&=&\dfrac{1\cdot 10^{-2}\times 8.5}{8.5+20}\\&\Rightarrow&\left[Cl^{-}\right]=2.98\cdot 10^{-3}mol\cdot L^{-1} \end{array}$

$\begin{array}{lcl} \left[Na^{+}\right]&=&\dfrac{C_{B}V_{B}}{V_{A}+V_{B}}\\&=&\dfrac{4.25\cdot 10^{-3}\times 20}{8.5+20}\\&\Rightarrow&\left[Na^{+}\right]=1.49\cdot 10^{-4}mol\cdot L^{-1} \end{array}$

$\left[H_{3}O^{+}\right]=10^{-7}mol\cdot L^{-1}$

$\left[OH^{-}\right]=10^{-7}mol\cdot L^{-1}$

Masse de chlorure de sodium

$NaCl$ dissoute à l'équivalence.

$\begin{array}{lcl} m_{NaCl}&=&n_{NaCl}\times M_{NaCl}\\&=&C_{A}V_{A}\times M_{NaCl}\\&=&1\cdot 10^{-2}\times 8.5\cdot 10^{-3}\times(23+35.5)\\&\Rightarrow&m_{NaCl}=4.97\,mg \end{array}$

Cette masse n'augmente pas après l'équivalence car elle dépend de la quantité d'hydroxyde de sodium dosée

Auteur:

Amary Thiam & Sidy Mouhamed Ndiaye

Ajouter un commentaire

form.antibot { display: none !important; } You must have JavaScript enabled to use this form.

Vous êtes ici

Notion d'acide fort et de base forte : Réaction entre acide fort et base forte - Ts

Formulaire de recherche

I. Acide fort

1. Étude d'un exemple : le chlorure d'hydrogène

1.1 Étude qualitative

1.2 Étude quantitative

2. Solutions aqueuses d'acides forts

2.1 Définition

2.2 Exemples d'acides forts

2.3 pHpH d'une solution d'acide fort

Remarque :

II. Base forte

1. Étude d'un exemple : l'hydroxyde de sodium NaOHNaOH

1.1 Étude qualitative

1.2 Étude quantitative

2. Solutions aqueuses de bases fortes

2.1 Définition

2.2 Exemples de bases fortes

Remarque :

III. Réaction entre acide fort et une base forte

1. Étude qualitative

2. Étude quantitative

2.1 Variation du pHpH au cours de la réaction

2.1.1 Étude expérimentale

2.1.2 Étude la courbe

2.2 Point d'équivalence

2.2.1 Définition

2.2.2 Détermination du point d'équivalence

IV. Applications aux dosages

1. Principe d'un dosage acido-basique

2. Dosage pH−pH- métrique

3. Dosage colorimétrique

4. Application : dosage d'une base forte par un acide fort

Exercice d'application

Solution

Ajouter un commentaire

Plain text

2.3 $pH$ d'une solution d'acide fort

1. Étude d'un exemple : l'hydroxyde de sodium $NaOH$

2.1 Variation du $pH$ au cours de la réaction

2. Dosage $pH-$ métrique