Vous êtes ici

Notion d'intensité et de tension - 2nd L

Classe:

Seconde

I. Intensité d'intensité du courant électrique

1. Notion d'intensité électrique

1.1 Variation des effets et intensité

Réalisons un circuit électrique constitué :

$-\$ d'un générateur

$-\$ de deux récepteurs : l'ampoule

$(L)$ , la cuve à l'électrolyse

$(C)$ , contenant de l'eau distillée

$-\$ d'un interrupteur

$(K)$

$-\$ reliés par des fils conducteurs

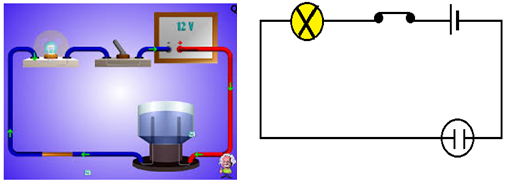
On ferme l'interrupteur la lampe reste éteinte, il ne passe rien dans la cuve

On ajoute quelques gouttes de soude dans l'eau de la cuve :

$-\$ l'ampoule s'allume

$-\$ des bulles de gaz se dégagent aux électrons de la cuve

Ces effets du courant deviennent plus importants que le courant est intense ou son intensité a augmenté

1.2 Définition de l'intensité

Si en une durée t exprimée en seconde(s).

$N$ nombre de charges qui traverse une section de conducteur métallique

Le débit de porteurs de charges est défini par la relation

$D=\dfrac{N}{t}$

Si ce débit est constant, l'intensité

$I$ d'un courant continu est le rapport de la valeur absolue de la quantité d'électricité

$Q$ sur la durée de passage

$t$

$\begin{array}{lcl} D&=&\dfrac{Q}{t}\\\\\text{or }Q&=&N_{e}\\\\\Rightarrow\,I&=&\dfrac{N_{e}}{t}\\\\\Rightarrow\,I&=&D_{e} \end{array}$

1.3 Ordre grandeur de quelques intensités

$\begin{array}{|l|l|l|l|l|l|} \hline \text{Foudre}&\text{Génératrice de}&\text{Démarreur}&\text{Plaque}&\text{Lampe}&\text{Montre}\\ &\text{centrale électrique}&\text{de voiture}&\text{ de cuisson}&\text{halogène}&\text{à quartz}\\ \hline \text{Jusqu'à }200KA&5KA&50A&2\text{ à }20A&1\text{ à }2A&\text{Quelques }nA\\ \hline \end{array}$

2. Mesure de l'intensité du courant électrique

2.1 Représentation des ampèremètres

L'ampèremètre est un appareil qui permet de mesurer l'intensité du courant électrique

On distingue deux types d'ampèremètres :

$-\$ les ampèremètres à aiguilles

$-\$ les ampèremètres numériques (ou digitaux)

Pour mesurer des courants d'intensité très faible ou déceler simplement le passage du courant électrique on utilise le galvanomètre

L'ampèremètre est schématisé par le symbole :

L'ampèremètre comporte deux parties essentielles :

$-\$ un cadran

$-\$ des calibres

$(3A.$

$1A...$ etc

$)$

Le calibre d'un ampèremètre indique l'intensité maximale pour laquelle l'aiguille est en fin de course

$-\$ des divisions

2.2 Branchement et précautions

2.2.1 Branchement

Pour mesurer l'intensité du courant électrique qui traverse un dipôle

$D$ placé dans un circuit

On ouvre :

$-\$ le circuit immédiatement avant (ou après)

$D$ et on intercale l'ampèremètre

$-\$ l'ampèremètre et le dipôle

$D$ sont en série.

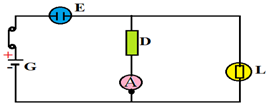
De nombreux appareils ampèremètres sont polarisés. Le courant électrique doit entrer dans l'ampèremètre par la borne positive et sortir par la borne négative

2.2.2 Précaution

Lors d'une mesure il est important pour ne pas détériorer l'ampèremètre d'essayer d'abord les calibres les plus élevés, on effectuera ensuite la mesure avec le calibre qui donne la déviation la plus nette.

2.3 Lecture et intensité de mesure

2.3.1 Lecture

Les grandeurs déviation

$n$ et l'intensité I sont proportionnelles et on associe

$\text{Calibre}\ \longrightarrow\ N\text{ avec }N\ :\ \text{nombre total de division}$

$I\ \longrightarrow\ n\text{ avec }n\ :\ \text{nombre de divisions lues}$

$I=\text{Calibre}\times\dfrac{n}{N}$

Exemple

Le cadran d'ampèremètre comporte

$100$ décisions équidistantes on l'utilise sur le calibre

$300\,mA.$

Quelle est la valeur de l'intensité du courant quand l'aiguille s'arrête sur la division

$80.$

Solution

La valeur de l'intensité du courant

$\begin{eqnarray} I&=&\text{Calibre}\times\dfrac{n}{N}\nonumber\\\\ &=&300\times\dfrac{80}{100}\nonumber\\\\\Rightarrow\,I&=&240mA \end{eqnarray}$

Remarque

Dans le cas des ampèremètres digitaux la valeur de l'intensité du courant est affichée directement Incertitude de mesure

2.3.2 Classe

La classe de l'ampèremètre est une donnée technique du constructeur permettant d'évaluer l'incertitude absolue sur la mesure de l'intensité

$\Delta I=\text{Classe}\times\dfrac{\text{Calibre}}{100}$

2.4 Présentation du résultat de la mesure de l'intensité

Par définition :

$I=I_{0}\pm\Delta I$ ou

$I=I_{0}-\Delta I\leq\,I\leq\,I_{0}+\Delta I$

3. Propriétés de l'intensité du courant électrique

3.1 Unicité de l'intensité du courant électrique dans un circuit en série

3.1.1 Observation

Les ampèremètres

$A_{1}$ ,

$A_{2}$ et

$A_{3}$ montrent les intensités

$I_{1}$ ,

$I_{2}$ et

$I_{3}$ on constate que les ampèremètres indiquent la même valeur

$I_{1}=I_{2}=I_{3}=I$

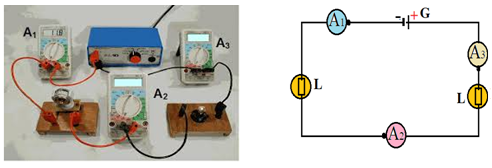
Mettre un dipôle supplémentaire en série dans le circuit produit une diminution de l'intensité

3.1.2 Conclusion

$-\$ Dans un circuit en série l'intensité du courant électrique est la même en tout point du circuit : c'est la loi de l'unicité de l'intensité du courant électrique.

$-\$ Quand on ajoute un récepteur en série dans le circuit l'intensité du courant électrique diminue

3.2 Loi des nœuds dans un circuit en dérivation

3.2.1 Observation

L'ampèremètre

$A_{1}$ mesure l'intensité du courant dans la branche principale

$A_{2}$ mesure l'intensité

$I_{2}$ du courant dans une branche en dérivation et

$A_{3}$ L'intensité

$I_{3}$ du courant dans une autre branche en dérivation

Nous constatons que

$I_{2}+I_{3}=I_{1}$

Si l'on devise un dipôle il ne fonctionne pas et l'autre continue à fonctionner

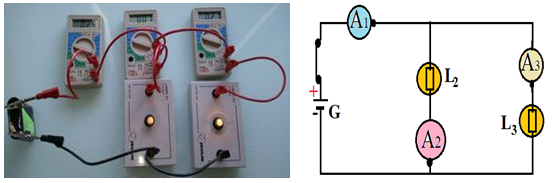
3.2.2 Conclusion

Dans un circuit en dérivation l'intensité du courant de la branche principale est égale à la somme des intensités des courants dans les branches en dérivation

Ce résultat ne généralise également au cas où plusieurs courant arrivent au nœud et ou plusieurs courants partent.

La somme des intensités des courants qui arrivent à un nœud est égale à la somme des intensités des courants qui partent c'est la loi des nœuds

II. Tension électrique

1. Notion de tension électrique

1.1 Observations

Dans une pile neuve il existe une importante dissymétrie entre les bornes plus et moins.

Sur la borne

$-$ se trouve un excès d'électrons et la borne

$+$ un déficit d'électrons

En revanche dans une pile usagée (utilisée) cette dissymétrie est très faible.

On dit que la tension entre les bornes de la pile neuve est supérieure à celle qui existe entre les bornes de la pile usagée

1.2 Définition

La tension électrique caractérise la dissymétrie électrique de deux points d'un circuit :

Elle est nécessaire pour qu'un courant circule enterre ces deux points

1.3 Tension électrique grandeur algébrique

Relions deux points

$A$ et

$B$ par un fil conducteur.

Si le courant circule de

$A$ vers

$B$ à travers ce conducteur nous dirons la tension

$U_{AB}$ entre

$A$ et

$B$ à travers ce conducteur est positive

$\left(U_{AB}>0\right)$

Si au contraire le courant circule de

$B$ vers

$A$ nous dirons que la tension

$U_{BA}$ entre

$A$ et

$B$ est négative

$\left(U_{AB}<0\right)$

S'il ne circule aucun courant, la tension est nulle

$(UAB=0)$

Conclusion :

La tension électrique entre deux points

$A$ et

$B$ d'un circuit est une grandeur algébrique

1.4 Tension représentée par une fléchée

Par convention on note

$U_{AB}$ la tension entre les points

$A$ et

$B$ et on le représente par un segment fléché vers

$A$

Cette flèche est dessinée à côté du symbole

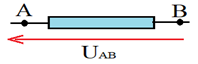
Remarque :

Cette flèche n'est pas vecteur mais seulement une représentation conventionnelle

1.5 Unités

Dans le Système International la tension s'exprime en volt

$(V)$

On utilise également les multiples et les sous-multiples du volt

Quelques multiples et sous-multiples du volt

$\begin{array}{|l|l|} \hline \text{Multiples}&\text{Sous-multiples}\\ \hline \text{Mégavolt : }1MV=10^{6}V&\text{Déci volt : }1dV=10^{-1}V\\ \text{Kilovolt : }1kV=10^{3}V&\text{Centi volt : }1cV=10^{-2}V\\ \text{Hecto volt : }1hV=10^{2}V&\text{Millivolt : }1mV=10^{-3}V\\ \text{décavolt : }1daV=10^{1}V&\text{Microvolt : }1\mu V=10^{-6}V\\ \hline \end{array}$

1.6 Ordre de Grandeurs de quelques tensions

$\begin{array}{|l|l|l|l|} \hline \text{Tensions aux bornes}&\text{Réseau d'éclairage}&\text{Ligne de transmission}&\text{Tension entre les nuages}\\ \text{d'une pile}&\text{urbain}&\text{électrique}&\text{pendant l'orage}\\ \hline 4.5V&110V\text{ à }220V&500000V&100.000.000V\\ \hline \end{array}$

2. Mesure de tension électrique

2.1 Utilisation du voltmètre

On distingue deux types de voltmètres pour la mesure des tensions électriques

$-\$ les voltmètres à aiguille

$-\$ les voltmètres numériques (digitaux)

Le voltmètre est schématisé par le symbole :

2.1.1 Le branchement du voltmètre

Le principe d'utilisation du voltmètre est la même que celui de l'ampèremètre a la différence que le voltmètre est branché en dérivation ou en parallèle

2.1.2 Lecture de la tension électrique

La tension mesurée aux bornes d'un dipôle à l'aide d'un voltmètre à aiguille a pour expression

$I=\text{Calibre}\times\dfrac{n}{N}$

$n$ : nombre de divisions devant lesquels s'immobilise l'aiguille

$N$ : nombre total de divisions sur le cadran

2.1.3 Incertitude de mesure

Tout comme l'intensité du courant électrique l'incertitude des classes que l'on commet en mesurant une tension électrique est définie par la relation suivante

$\boxed{\Delta U=\dfrac{\text{Calibre}\times\text{Clase}}{100}}$

La précision de la mesure est donnée par

$\dfrac{\Delta U}{U}$

2.2 Utilisation l'oscilloscope

On peut mesurer la tension entre deux points

$A$ et

$B$ a l'aide de l'oscilloscope

Mesure

Soit un dipôle de borne

$A$ et

$B$ relions

$A$ à une borne

$Y$ et

$B$ a la masse

$M$ : Le spot initialement en

$0$ subit une déviation

$Y$

Nous poserons :

$U_{AB}=Ky$

$K$ est la sensibilité verticale en

$V/div$

$U_{AB}$ supérieur à

$0$ ,

$y$ supérieur a aussi à

$0$

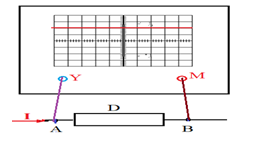
La lecture de la déviation

$y$ permet de calculer

$U_{AB}$ la valeur de

$k$ lue directement

Remarque

On peut vérifier facilement la tension entre deux points d'un même fil de connexion est nul

3. Propriétés des tensions

3.1 Loi d'additivité des tensions

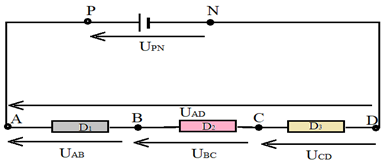
Mesurons les tensions

$U_{PN}$ ,

$U_{AD}$ ,

$U_{AB}$ ,

$U_{BC}$ et

$U_{CD}$

On constate :

$U_{PN}=U_{AD}=U_{AB}+U_{BC}+U_{CD}$

La tension aux bornes d'une association de dipôles montés en série est égale à la somme des tensions aux bornes de chacun des dipôles

3.2 Unicité de la tension entre deux points

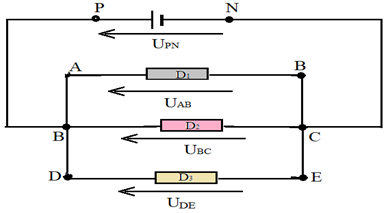
Mesurons les tensions

$U_{PN}$ ,

$U_{AB}$ ,

$U_{BC}$ et

$U_{DE}$

On constate :

$U_{PN}=U_{AB}=U_{BC}=U_{DE}$

La tension est la même aux bornes de plusieurs dipôles montés en dérivation ou parallèle

4. Tensions variables

4.1 Tension continue et tension variable

Une tension qui ne varie pas au cours du temps ni en grandeur ni en signe est dite continue

En revanche quand le signe ou la valeur de la tension change elle est variable

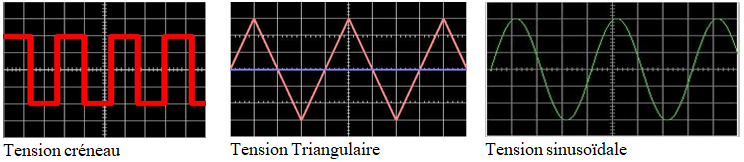
Exemples de tensions variables

Certains générateurs sont conçus pour fournir des tensions variables particulaires dont la trace sur l'eau a la forme

Remarque

Certaines Tensions variables reprennent la même valeur a un intervalle de temps régulier elles sont dites périodiques

4.2 Tension alternative

Une Tension alternative est une tension qui prend alternativement des valeurs positives et négatives

Exemples :

tension créneau, tension triangulaire et tension sinusoïdale

4.3 Tension sinusoïdale

4.3.1 Définition

Une tension est dite sinusoïdale si la courbe représentant la tension

$U$ en fonction du temps est une courbe régulière appelé sinusoïde

4.3.2 Caractéristiques d une tension sinusoïdale

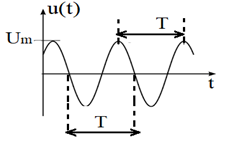
La tension sinusoïdale est caractérisée par :

La période

$T$ ou la fréquence

$N$

La période

$T$ est plus petit intervalle de temps au bout duquel la tension se reproduit identique à elle-même

La fréquence

$N$ est le nombre de périodes par unité de temps

$N=\dfrac{1}{T}$

Elle s'exprime en Hertz

$(Hz)$

La tension maximale ou la tension efficace

La tension maximale se déduit de la déviation maximale

$M_{\text{MAX}}=Ky_{\text{MAX}}$

La tension maximale est liée à la tension efficace par la relation :

$U_{\text{MAX}}=U\sqrt{2}$

$U_{\text{MAX}}$ et

$U$ étant respectivement la tension maximale et la tension efficace

5. Convention récepteur et mesure de sécurité

5.1 Convention Récepteur

Considérons un dipôle

$D$ parcouru par un courant

Soient

$A$ et

$B$ les deux bornes du dipôle

Orientons arbitrairement le dipôle de

$A$ vers

$B$ pour algébriser l'intensité du courant traversant le dipôle que nous noterons alors

$U_{AB}$

Dans la convention récepteur la flèche qui symbolise l'orientation du dipôle pour l'intensité et celle qui représente la tension à considérer sont de sens contraire

5.2 Mesure de Sécurité

5.2.1 Le danger du courant électrique de la tension électrique

Dans une installation domestique la tension aux bornes de la prise est de

$220V$ à

$380V$

Le seuil de tension dangereuse (mortelle) est de

$50V$ et de

$24V$ dans un local humide.

La tension dans les branchements domestiques étant de

$220V$ à

$380V$ , il y'a un danger réel à toucher un fil de phase

L'électrocution se produit lorsqu'on touche un fil de phase.

N'étant pas soi-même isolé du sol. Les risques d'électrocution sont plus grands lorsque l'on est mouillé ou quand le sol est mouillé

5.2.2 Les règles de sécurité

$-\$ L'isolation des conducteurs doit être rigoureuse

$-\$ S'abstenir de manipuler des appareils électriques quand on est mouillé.

Pour changer une ampoule de salle de bain prendre soin de très isoles du sol de manière qu'entre les pieds et le sol aucun corps ne puisse conduire des charges électriques.

$-\$ Débrancher tout appareil électrique avant démontage

$-\$ vérifier que la fiche de terre des appareils qui en comportent est bien mise à la terre

III. Loi d'ohm

1. Caractéristique d'un résistor ou d'un conducteur ohmique

1.1 Définition

On appelle caractéristique d'un dipôle la représentation (très souvent expérimentale) d'une relation fonctionnelle entre deux grandeurs physiques

En électricité quand les grandeurs sont la tension

$U$ et l'intensité

$I$

$-\$ La caractéristique tension-intensité d'un dipôle est la courbe représentant les variations de l'intensité

$I$ dans le dipôle en fonction de la tension

$U$ à ses bornes

$I=f(u)$

$-\$ La caractéristique intensité-tension d'un dipôle est la courbe représentant les variations de la tension

$U$ à ses bornes en fonction de l'intensité

$I$ du courant qui le traverse

1.2 Expérience

Montage

Considérons le montage suivant

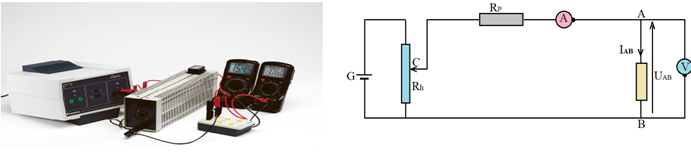
le rhéostat

$R_{h}$ on fait varier

$I_{AB}$ lue sur l'ampèremètre pour chaque valeur de

$I_{AB}$ on lit

$U_{AB}$ sur le voltmètre Tracé de la caractéristique

En agissant sur

Une expérience permet d'obtenir le tableau de valeurs suivantes

$\begin{array}{|l|c|c|c|c|c|c|} \hline U_{AB}(V)&0&0.9&1.5&2.4&3.0&3.7\\ \hline I_{AB}(mA)&0&30&50&80&100&123\\ \hline \end{array}$

Ce tableau nous permet de tracer la caractéristique intensité-tension

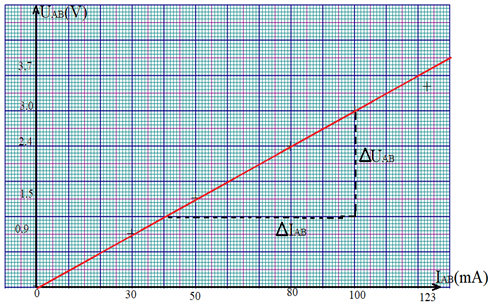
La caractéristique intensité-tension d'un résistor ou conducteur ohmique est une droite passant par l'origine limitée à la valeur maximale de

$I_{AB}$ supportable par le résistor le résistor est un dipôle passif linéaire

On obtiendrait la même courbe en intervertissant les bornes du résistor

$U_{AB}=f\left(I_{AB}\right)$ le résistor est un dipôle symétrique

Le coefficient directeur de la droite représente une caractéristique du conducteur ohmique : la résistance notée

$R$

La résistance électrique traduit la propriété des matériaux à s'opposer au déplacement des électrons

Dans l'expérience décrite :

$\begin{eqnarray} R&=&\dfrac{\Delta U_{AB}}{\Delta I_{AB}}\nonumber\\\\ &=&\dfrac{3-1.2}{(100-40)\cdot 10^{-3}}\nonumber\\\\\Rightarrow\,R&=&30\Omega \end{eqnarray}$

2. Loi d'ohm

Énoncé :

La tension appliquée aux bornes d'un conducteur ohmique est une fonction linéaire de l'intensité qui le traverse

$\boxed{U=RI}$

Ajouter un commentaire

form.antibot { display: none !important; } You must have JavaScript enabled to use this form.

Vous êtes ici

Notion d'intensité et de tension - 2nd L

Formulaire de recherche

I. Intensité d'intensité du courant électrique

1. Notion d'intensité électrique

1.1 Variation des effets et intensité

1.2 Définition de l'intensité

1.3 Ordre grandeur de quelques intensités

2. Mesure de l'intensité du courant électrique

2.1 Représentation des ampèremètres

2.2 Branchement et précautions

2.2.1 Branchement

2.2.2 Précaution

2.3 Lecture et intensité de mesure

2.3.1 Lecture

Exemple

Solution

Remarque

2.3.2 Classe

2.4 Présentation du résultat de la mesure de l'intensité

3. Propriétés de l'intensité du courant électrique

3.1 Unicité de l'intensité du courant électrique dans un circuit en série

3.1.1 Observation

3.1.2 Conclusion

3.2 Loi des nœuds dans un circuit en dérivation

3.2.1 Observation

3.2.2 Conclusion

II. Tension électrique

1. Notion de tension électrique

1.1 Observations

1.2 Définition

1.3 Tension électrique grandeur algébrique

Conclusion :

1.4 Tension représentée par une fléchée

Remarque :

1.5 Unités

1.6 Ordre de Grandeurs de quelques tensions

2. Mesure de tension électrique

2.1 Utilisation du voltmètre

2.1.1 Le branchement du voltmètre

2.1.2 Lecture de la tension électrique

2.1.3 Incertitude de mesure

2.2 Utilisation l'oscilloscope

Remarque

3. Propriétés des tensions

3.1 Loi d'additivité des tensions

3.2 Unicité de la tension entre deux points

4. Tensions variables

4.1 Tension continue et tension variable

Remarque

4.2 Tension alternative

Exemples :

4.3 Tension sinusoïdale

4.3.1 Définition

4.3.2 Caractéristiques d une tension sinusoïdale

5. Convention récepteur et mesure de sécurité

5.1 Convention Récepteur

5.2 Mesure de Sécurité

5.2.1 Le danger du courant électrique de la tension électrique

5.2.2 Les règles de sécurité

III. Loi d'ohm

1. Caractéristique d'un résistor ou d'un conducteur ohmique

1.1 Définition

1.2 Expérience

2. Loi d'ohm

Ajouter un commentaire

Plain text