Vous êtes ici

Solution des exercices : Équilibre d'un solide soumis à des forces - 2nd S

Classe:

Seconde

Exercice 1

1) Un solide $S$ de poids $P=100\;N$ est maintenu en équilibre sur un plan incliné d'un angle $\alpha$ par rapport à l'horizontal grâce à un fil.

Le support du plan incliné $AB$ est lisse.

1.1) Bilan des forces appliquées au solide $(S).$

Le solide est soumis à : son poids ; $\vec{P}$ la tension du fil $\vec{T}$ et à la réaction du plan $\vec{R}.$

1.2) Représentons ces forces puis déterminons leurs intensités par la méthode analytique.

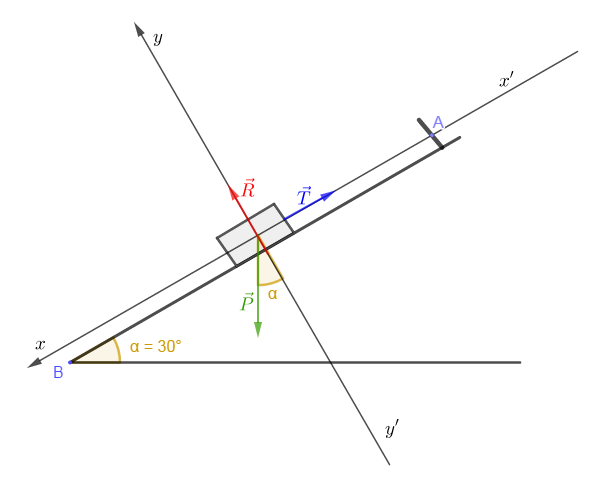
La condition d'équilibre appliquée au solide $(S)\ :$

$$\vec{P}+\vec{T}+\vec{R}=\vec{0}$$

En projetant cette relation vectorielle suivant les axes, on obtient :

$\begin{array}{rcl} *\ \ x'x\ :\ -T+P\sin\alpha+0=0&\Rightarrow&T=P\sin\alpha\\ \\&\Rightarrow&T=100\sin 30^{\circ}\\ \\&\Rightarrow&T=50\;N\end{array}$

Ainsi, $\boxed{T=50\;N}$

$\begin{array}{rcl} *\ \ y'y\ :\ 0-P\cos\alpha+R=0&\Rightarrow&R=P\cos\alpha\\ \\&\Rightarrow&R=100\cos 30^{\circ}\\ \\&\Rightarrow&R=86.6\;N\end{array}$

D'où, $\boxed{R=86.6\;N}$

2) Un solide $(S')$ de poids $P'$ glisse sur un support oblique $A'B'.$

La partie $A'C$ de ce plan est rugueuse et la partie $CB'$ lisse.

a) Le solide $S'$ s'arrête entre $A'\ $ et $\ C.$

Exprimons les composantes tangentielle $f$ et normale $R_{n}$ de la réaction du plan $A'C$ en fonction de $P'\ $ et $\ \alpha$

La condition d'équilibre appliquée au solide $(S')\ :$

$$\vec{f}+\vec{P'}+\vec{R}_{n}=\vec{0}$$

En projetant cette relation vectorielle suivant les axes, on obtient :

$*\ \ x'x\ :\ -f+P'\sin\alpha+0=0\ \Rightarrow\ f=P'\sin\alpha$

$*\ \ y'y\ :\ 0-P'\cos\alpha+R_{n}=0\ \Rightarrow\ R_{n}=P'\cos\alpha$

La direction de cette force de réaction est sécante à celle du vecteur poids du solide $S'.$

b) On déplace le solide $S'$ et on le pose sur le plan $CB'$ au-delà du point $C$

Il glisse puis se met en contact avec un ressort de constante de raideur $k.$

Le solide $S'$ s'immobilise alors quand le ressort est comprimé d'une quantité $x.$

Représentons les forces s'exerçant sur le solide $S'$ dans cet état d'équilibre

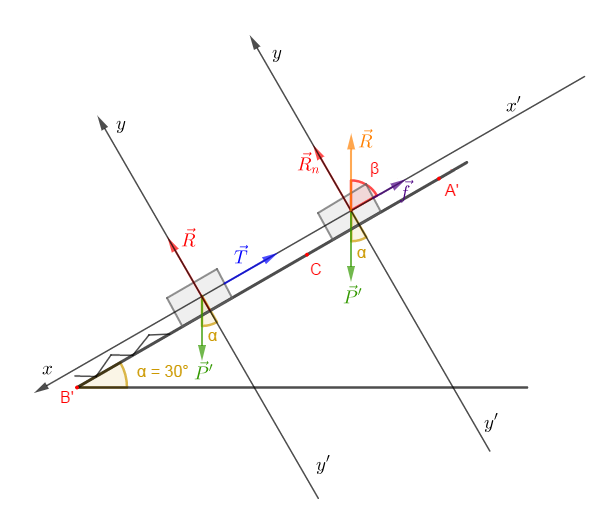
Exprimons l'intensité de la force exercée par le ressort sur $S'$ en fonction de $P'\ $ et $\ \alpha.$

La condition d'équilibre appliquée au solide $(S')\ :$

$$\vec{P'}+\vec{T}+\vec{R}=\vec{0}$$

En projetant cette relation vectorielle suivant l'axe, on obtient :

$*\ \ x'x\ :\ -T+P'\sin\alpha+0=0\ \Rightarrow\ T=P'\sin\alpha$

c) Considérant les résultats a) et b), exprimons l'intensité $f$ des forces de frottement du plan $A'C$ en fonction de $x$ et de $k.$

$\left\lbrace\begin{array}{rcl} f&=&P'\sin\alpha\\\\T&=&P'\sin\alpha\end{array}\right.\ \Rightarrow\ f=T=kx$

Ainsi, $\boxed{f=kx}$

d) Calculons dans l'ordre $f\;,\ R_{n}$, la réaction $R$ du plan $A'C$, et la masse $m'$ du solide $S'.$

Soit :

$\begin{array}{rcl} f&=&kx\\\\&=&50\times8\cdot 10^{-2}\\\\&=&4\end{array}$

Alors, $\boxed{f=4\;N}$

Soit :

$\begin{array}{rcl} R_{n}=P'\cos\alpha\quad\text{or, }\ T=f=P'\sin\alpha&\Rightarrow&P'=\dfrac{f}{\sin\alpha}\\ \\&\Rightarrow&R_{n}=f\dfrac{\cos\alpha}{\sin\alpha}\\ \\&\Rightarrow&R_{n}=4\times\dfrac{\cos 30^{\circ}}{\sin 30^{\circ}}\\ \\&\Rightarrow&R_{n}=6.9\end{array}$

Ainsi, $\boxed{R_{n}=6.9\;N}$

On a :

$\begin{array}{rcl} f=P'\sin\alpha=m'g\sin\alpha&\Rightarrow&m'=\dfrac{f}{g\sin\alpha}\\ \\&\Rightarrow&m'=\dfrac{4}{10\times\sin 30^{\circ}}\\ \\&\Rightarrow&m'=0.8\end{array}$

Donc, $\boxed{m'=0.8\;kg}$

e) Calculons l'angle $\beta$ que fait la direction de la réaction du plan, $A'C$ avec celle du plan incliné $A'B'.$

On a :

$\begin{array}{rcl} \tan\beta=\dfrac{R_{n}}{f}&\Rightarrow&\beta=\tan^{-1}\left(\dfrac{R_{n}}{f}\right)\\ \\&\Rightarrow&\beta=\tan^{-1}\left(\dfrac{6.9}{4}\right)\\ \\&\Rightarrow&\beta=60^{\circ}\end{array}$

Ainsi, $\boxed{\beta=60^{\circ}}$

Exercice 2

Un véhicule de masse $820\;kg$ est immobilisé sur un plan incliné à l'aide d'un câble fixé au point $A.$

Les frottements sur le sol sont négligés. Le plan est incliné de $30^{\circ}$ par rapport au plan horizontal.

1) Faisons le bilan des forces s'exerçant sur le véhicule.

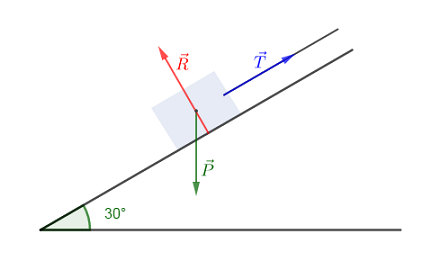
Le véhicule est soumis à : son poids $\vec{P}$, la tension $\vec{T}$ du câble et la réaction $\vec{R}$ du plan incliné

2) Déterminons par méthode graphique les intensités des forces inconnues.

On construit le polygone des forces :

$\begin{array}{rcl}\vec{P}+\vec{T}+\vec{R}=\vec{0}&\Rightarrow&\vec{P}=-(\vec{T}+\vec{R})\\ \\&\Rightarrow&\vec{P}=-\vec{T}-\vec{R}\end{array}$

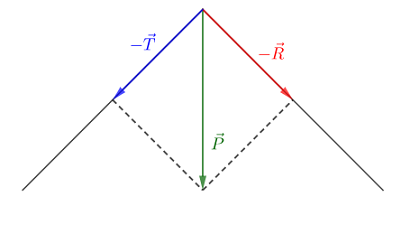
Soit : $P=M.g=820\times 10=8200$

Donc, $\boxed{P=8.2\cdot 10^{3}\;N}$

D'après l'échelle, on :

$\dfrac{x\;cm}{F}=\dfrac{1\;cm}{2000}\ \Rightarrow\ x=\dfrac{1\;cm}{2000}\times F$

Pour $F=P$, on a : $x=\dfrac{1\;cm}{2000\;N}\times 8.2\cdot 10^{3}\;N=4.1\;cm$

Après projection, on obtient respectivement les mesures suivantes des vecteurs : $-\vec{T}\ $ et $\ -\vec{R}$

$$x_{T}=2.1\;cm\quad\text{et}\quad x_{R}=3.4\;cm$$

Comme $\dfrac{x\;cm}{F}=\dfrac{1\;cm}{2000}$ alors, $F=\dfrac{2000\;N}{1\;cm}\times x\;cm$

Pour $F=R$, on obtient : $R=\dfrac{2000\;N}{1\;cm}\times 3.4\;cm=6800\;N$

Donc, $\boxed{R=6.80\cdot 10^{3}\;N}$

Pour $F=T$, on a : $T=\dfrac{2000\;N}{1\;cm}\times 2.1\;cm=4200\;N$

Ainsi, $\boxed{T=4.2\cdot 10^{3}\;N}$

3) Retrouvons ces intensités par méthode analytique

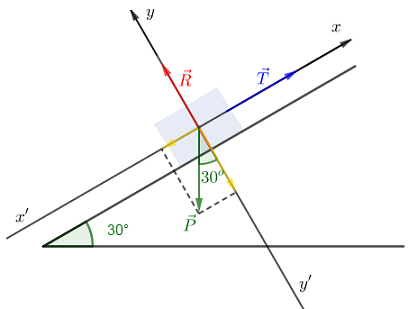
La condition d'équilibre appliquée au solide au véhicule est donnée par :

$$\vec{P}+\vec{T}+\vec{R}=\vec{0}$$

En projetant cette relation vectorielle suivant les axes, on obtient :

$\begin{array}{rcl} *\ x'x\ :\ -P\sin 30^{\circ}+T+0=0&\Rightarrow&T=P\sin 30^{\circ}\\ \\&\Rightarrow&T=8.2\cdot 10^{3}\sin 30^{\circ}\\ \\&\Rightarrow&T=4.1\cdot 10^{3}\;N\end{array}$

$\begin{array}{rcl}*\ y'y\ :\ -P\cos 30^{\circ}+0+R=0&\Rightarrow&R=P\cos 30^{\circ}\\ \\&\Rightarrow&R=8.2\cdot 10^{3}\cos 30^{\circ}\\ \\&\Rightarrow&R=7.1\cdot 10^{3}\;N\end{array}$

Exercice 3

On dispose de 2 ressorts $(R_{1})\ $ et $\ (R_{2})$ de longueur à vide $l_{01}$ de $10\;cm$ et s'allonge de $1\;cm$ pour une force appliquée de $1\;N.$ Le ressort $(R_{2})$ a une longueur à vide $l_{02}=15\;cm$ et s'allonge de $4\;cm$ pour une force appliquée de $1\;N.$

On les réunit à un anneau de poids et de dimensions négligeables. Les 2 autres extrémités des ressorts sont fixées à 2 crochets distants de $30\;cm.$

Soient $l_{1}\ $ et $\ l_{2}$ les longueurs respectives des ressorts $(R_{1})\ $ et $\ (R_{2}).$

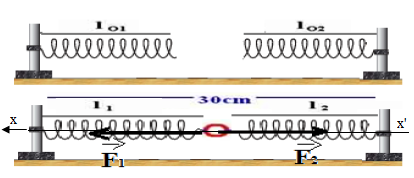
Calculons la longueur de chaque ressort $l_{1}\ $ et $\ l_{2}$

Pour cela, on détermine d'abord les raideurs $k_{1}\ $ et $\ k_{2}$

On a : $F=k\Delta l\ \Rightarrow\ k=\dfrac{F}{\Delta l}$

Alors,

$\begin{array}{rcl} k_{1}&=&\dfrac{F_{1}}{\Delta l}\\ \\&=&\dfrac{1}{10^{-2}}\\ \\=100\;N.m^{-1}\end{array}$

Donc, $\boxed{k_{1}=100\;N.m^{-1}}$

$\begin{array}{rcl} k_{2}&=&\dfrac{F_{2}}{\Delta l}\\ \\&=&\dfrac{1}{4.10^{-2}}\\ \\&=&25\;N.m^{-1}\end{array}$

Ainsi, $\boxed{k_{2}=25\;N.m^{-1}}$

L'anneau est en équilibre, la condition d'équilibre s'écrit alors :

$$\vec{F}_{1}+\vec{F}_{2}=\vec{0}$$

Ce qui donne, après projection sur l'axe $(x'x)\ :$

$\begin{array}{rcl} F_{1}-F_{2}=0&\Rightarrow&k_{1}(l_{1}-l_{01})-k_{2}(l_{2}-l_{02})=0\\ \\&\Rightarrow&100(l_{1}-10)-25(l_{2}-15)=0\\ \\&\Rightarrow&100l_{1}-25l_{2}=625\\ \\&\Rightarrow&4l_{1}-l_{2}=25\end{array}$

On obtient alors une première équation : $4l_{1}-l_{2}=25$

Par ailleurs, on sait que : $l_{1}+l_{2}=30$

Ainsi, on obtient le système d'équations suivant :

$$\left\lbrace\begin{array}{rcl} 4l_{1}-l_{2}&=&25\quad(1)\\l_{1}+l_{2}&=&30\quad(2)\end{array}\right.$$

Par suite,

$\begin{array}{rcl}(1)+(2)&\Rightarrow&5l_{1}=55\\ \\&\Rightarrow&l_{1}=\dfrac{55}{5}\\ \\&\Rightarrow&l_{1}=11\end{array}$

Donc, $\boxed{l_{1}=11\;cm}$

Comme $l_{1}+l_{2}=30$ alors,

$\begin{array}{rcl} l_{2}&=&30-l_{1}\\\\&=&30-11\\\\&=&19\end{array}$

D'où, $\boxed{l_{2}=19\;cm}$

Calculons les forces de tension $F_{1}\ $ et $\ F_{2}$ des ressorts

Soit :

$\begin{array}{rcl} F_{1}&=&k_{1}(l_{1}-l_{01})\\\\&=&100(11-10).10^{-2}\\\\&=&1\end{array}$

Donc, $\boxed{F_{1}=1\;N}$

On a :

$\begin{array}{rcl} F_{2}&=&k_{2}(l_{2}-l_{02})\\\\&=&25(19-15).10^{-2}\\\\&=&1\end{array}$

Alors, $\boxed{F_{2}=1\;N}$

Exercice 4

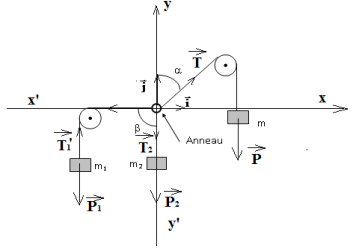
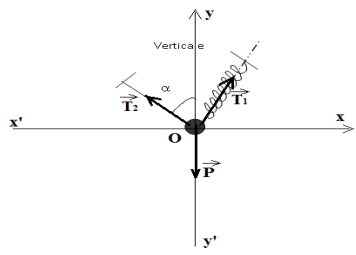
1. Représentation sur un schéma des forces qui s'exercent sur l'anneau( Voir schéma)

2. Rappelons la relation vectorielle que l'on peut écrire à l'équilibre.

$\overrightarrow{T}_{1}+\overrightarrow{T}_{2}+\overrightarrow{T}_{3}=\overrightarrow{O}$

3. Donnons l'expression de toutes les forces agissant sur l'anneau en fonction des vecteurs $\vec{i}$ et $\vec{j}$

$\overrightarrow{T}_{1}=T_{1}\vec{i}$ ;

$\overrightarrow{T}_{2}=-\overrightarrow{T}_{2}=-T_{2}\vec{j}$ ;

$\overrightarrow{T}=(T\sin\alpha)\vec{i}+(T\cos\alpha)\vec{j}$

Intensité de chacune des forces.

La condition d'équilibre appliquée à la masse $m_{1}$ :

$\begin{array}{rcl} \overrightarrow{T'}_{1}+\overrightarrow{P}_{1}&=&\overrightarrow{0}\\\Rightarrow\;T'_{1}-P_{1}&=&0\\\Rightarrow\;T'_{1}&=&P_{1}\\\text{or }T'_{1}&=&T_{1}\\\Rightarrow\;T_{1}&=&m_{1}g\\&=&150\cdot10^{-3}\times10\\\Rightarrow\boxed{T_{1}=1.5\,N} \end{array}$

$\begin{array}{rcl} T_{2}&=&m_{2}g\\&=&100\cdot10^{-3}\times10\\\Rightarrow\;T_{2}&=&1\,N \end{array}$

$\begin{array}{rcl}T&=&\sqrt{T_{x}^{2}+T_{y}^{2}}\\&=&\sqrt{T_{1}^{2}+T_{2}^{2}}\\&=&\sqrt{1.5^{2}+1^{2}}\\\Rightarrow\boxed{T=1.8\,N} \end{array}$

4. Déduisons $2$ équations permettant de calculer $\alpha$ et $m$

$\begin{array}{rcl} \overrightarrow{T}_{1}+\overrightarrow{T}_{2}+\overrightarrow{T}=\overrightarrow{0}\\\\&\Rightarrow\left\lbrace\begin{array}{lcl} -T_{1}-0+T\sin\alpha&=&0\\ 0-T_{2}+T\cos\alpha&=&0 \end{array}\right.\\\\&\Rightarrow\left\lbrace\begin{array}{lcl} mg\sin\alpha&=&m_{1}g\quad(1)\\ mg\cos\alpha&=&m_{2}\quad(2) \end{array}\right.\\\\&\Rightarrow\left\lbrace\begin{array}{lcl} m\sin\alpha&=&m_{1}\quad(1)\\ m\cos\alpha&=&m_{2}\quad(2) \end{array}\right. \end{array}$

5. Calcul de $\tan\alpha$ pour et déduction la valeur de $\alpha$ puis de $m.$

$\begin{array}{rcl} \left\lbrace\begin{array}{lcl} m\sin\alpha&=&m_{1}\quad(1)\\ m\cos\alpha&=&m_{2}\quad(2) \end{array}\right.\ ; \\\\\dfrac{(1)}{(2)}\Rightarrow\dfrac{m\sin\alpha}{m\cos\alpha}&=&\dfrac{m_{1}}{m_{2}}\\\Rightarrow\tan\alpha&=&\dfrac{m_{1}}{m_{2}}\\&=&\dfrac{150}{100}\\\Rightarrow\tan\alpha&=&1.5\\\Rightarrow\alpha&=&\tan^{-1}1.5\\\Rightarrow\boxed{\alpha=56.3^{\circ}} \end{array}$

$\begin{array}{rcl} m\sin\alpha&=&m_{1}\\\\\Rightarrow\;m&=&\dfrac{m_{1}}{\sin\alpha}\\&=&\dfrac{150}{\sin56.3^{\circ}}\\\\\Rightarrow&\boxed{m=180\,g} \end{array}$

Exercice 5

I.1.Donnons l'expression de $T$ en fonction de $K$ ; $L$ et $L_{0}$

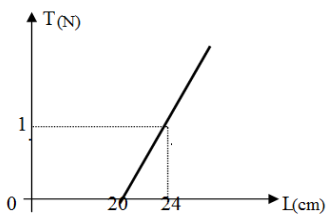
$T=K(L-L_{0})$

2. Déduisons à partir du graphique :

a. La raideur $K$du ressort en $N\cdot m^{-1}$

Le graphe représentant $T=f(L)$ est une droite de coefficient directeur $K$

$\begin{array}{rcl} K&=&\dfrac{\Delta T}{\Delta L}\\&=&\dfrac{1-0}{((24-20)}\cdot10^{-2}\\\Rightarrow\boxed{K=25\,N\cdot m^{-1}} \end{array}$

b. La longueur $L_{0}$ du ressort en $cm$

$\begin{array}{rcl} T&=&0\\\Rightarrow\;K\left(L-L_{0}\right)&=&0\\\Rightarrow\;L-L_{0}&=&0\\\Rightarrow\;L&=&\boxed{L_{0}=20\,cm} \end{array}$

II. 1. Représentons les forces exercées sur le solide à l'équilibre.

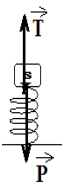
2.Calcul de la tension du ressort.

$\begin{array}{rcl} T&=&K\left|L-L_{0}\right|\\&=&25|18-20|\cdot 10^{-2}\\\Rightarrow\boxed{T=0.5\,N} \end{array}$

3. Déduction de la masse $m$ du solide $(S).$

La condition d'équilibre appliquée au solide s'écrit :

$\begin{array}{rcl} \overrightarrow{P}+\overrightarrow{T}&=&\overrightarrow{0}\\\Rightarrow\overrightarrow{ -P}+T&=&0\\\Rightarrow\;T&=&P\\\Rightarrow\;T&=&mg\\\Rightarrow\;m&=&\dfrac{T}{g}\\&=&\dfrac{0.5}{9.8}\\\Rightarrow\;m&=&0.051\,kg\\\Rightarrow\boxed{m=51\,g} \end{array}$

Exercice 6

1) Représentation des forces exercées sur le corps $(C).$

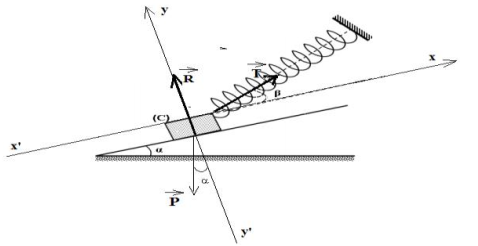
2 Écrivons la condition d'équilibre du corps $(C).$

$\overrightarrow{P}+\overrightarrow{T}+\overrightarrow{R}=\overrightarrow{0}$

3. Détermination la valeur de la tension $T$ du ressort.

En la relation vectorielle suivant l'axe $x'x$, il vient :

$\begin{array}{rcl} -P\sin\alpha+T\cos\beta+0&=&0\\\Rightarrow\;T\cos\beta&=&P\sin\alpha\\\Rightarrow\;T&=&\dfrac{P\sin\alpha}{\cos\beta}\\&=&\dfrac{20\times\sin30^{\circ}}{\cos15^{\circ}}\\\Rightarrow\boxed{T=10.6\,N} \end{array}$

4. Déduisons sa longueur $L$

$\begin{array}{rcl} T&=&K\left(L-L_{0}\right)\\\Rightarrow\;L-L_{0}&=&\dfrac{T}{K}\\\Rightarrow\;L&=&\dfrac{T}{K}+L_{0}\\&=&\dfrac{10.6} {500}+0.20\\\Rightarrow\;L&=&0.22\,m\\\Rightarrow\boxed{L=22\,cm} \end{array}$

Écrivons nouvelle condition d'équilibre du corps $(C)$

Déduisons la valeur de la force de frottement $f$

En la relation vectorielle suivant l'axe $x'x$, il vient :

$\begin{array}{rcl} -P\sin\alpha+T\cos\beta+f&=&0\\\Rightarrow\;f&=&P\sin\alpha-T\cos\beta\\&=&20\sin30^{\circ}-8.4\cos15^{\circ}\\\Rightarrow\boxed{f=} \end{array}$

Exercice 7

I. 1.a. Établissons l'expression de $k$ en fonction de $m_{1}$ ; $m_{2}$ ; $g$ ; $L_{1}$ et $L_{2}$ et montrons que

$K=\dfrac{\left(m_{2}-m_{1}\right)}{L_{2}-L_{1}}g$

Le solide est en équilibre sous l'action de son poids et de la tension du ressort, la condition d'équilibre s'écrit :

$\begin{array}{rcl} \overrightarrow{P}+\overrightarrow{P}&=&\overrightarrow{0}\\\Rightarrow\;-P+t&=&0\\\Rightarrow\;T&=&P\\\Rightarrow\boxed{\left(L-L_{0}\right)=mg} \end{array}$

$\begin{array}{rcl} \left\lbrace\begin{array}{lcl} K\left(L_{2}-L_{0}\right)&=&m_{2}g\quad(1)\\ K\left(L_{1}-L_{0}\right)&=&m_{1}g\quad(2) \end{array}\right.\\\\(1)-(2)\Rightarrow\;K\left(L_{2}-L_{0}\right)-K\left(L_{1}-L_{0}\right)&=&m_{2}g-m_{1}g\\\Rightarrow\;K\left(L_{2}-L_{1}\right)&=&\left(m_{2} m_{1}\right)g\\\Rightarrow\boxed{K=\dfrac{\left(m_{2}-m_{1}\right)}{L_{2}-L1}g} \end{array}$

Calcul de sa valeur en $N\cdot m^{-1}$

$\begin{array}{rcl} K&=&\dfrac{\left(m_{2}m_{1}\right)}{L_{2}L_{1}}g\\&=&\dfrac{(175-100)\cdot10^{-3}}{(23-20)}\cdot10^{-2}\times10\\\Rightarrow\boxed{K=25\,N\cdot m^{-1}} \end{array}$

b. Déduisons de la longueur initiale $L_{0}$ du ressort

$\begin{array}{rcl} K\left(L_{1}-L_{0}\right)&=&m_{1}g\\\Rightarrow\;L_{1}-L_{0}&=&\dfrac{m_{1}g}{K}\\\Rightarrow\;L_{0}&=&L_{1}-\dfrac{m_{1}g}{K}\\&=&0.20 \dfrac{100\cdot10^{-3}\times 10}{25}\\\Rightarrow\;L_{0}&=&0.16\\\Rightarrow\boxed{L_{0}=16\,cm} \end{array}$

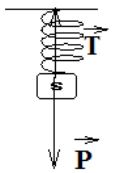
II. 1Représentons toutes les forces exercées sur $(S')$

II.2. Établissement en fonction de $m'$, $g$ et $\alpha$ :

La condition d'équilibre appliquée au solide $\left(S'\right)$ s'écrit :

$\overrightarrow{P}+\overrightarrow{T}_{1}+\overrightarrow{T}_{2}=\overrightarrow{0}$

En projetant la relation vectorielle suivant les axes,il vient :

$\begin{array}{rcl} \left\lbrace\begin{array}{lcl} m'g&=&T_{1}\cos\left(90^{\circ}-\alpha\right)+T_{2}\cos\alpha\\ 0&=&T_{1}\sin\left(90^{\circ}-\alpha\right)-T_{2}\sin\alpha \end{array}\right.\\\\\text{or }\cos\left(90^{\circ}-\alpha\right)=\sin\alpha\text{ et }\sin\left(90^{\circ} -\alpha\right)=\cos\alpha\\\\\Rightarrow\left\lbrace\begin{array}{lcl} m'g&=&T_{1}\sin\alpha+T_{2}\cos\alpha\\ 0&=&T_{1}\cos\alpha-T_{2}\sin\alpha \end{array}\right. \end{array}$

2.1 La tension de ressort $T_{1}$

$\begin{array}{rcl} \Rightarrow\left\lbrace\begin{array}{lcl} m'g&=&T_{1}\sin\alpha+T_{2}\cos\alpha\quad(1)\\ 0&=&T_{1}\cos\alpha-T_{2}\sin\alpha\quad(2) \end{array}\right. :\\ (1)\times\sin\alpha (2)\times\cos\\\Rightarrow\;m'g\sin\alpha&=&T_{1}\sin^{2}\alpha+T_{1}\cos^{2}\alpha\\\Rightarrow\;m'g\sin\alpha&=&T_{1}\left(\sin^{2}\alpha+\cos^{2}\alpha\right)\\\Rightarrow\boxed{T_{1}=m'g\sin\alpha} \end{array}$

2.2 La tension du fil $T_{2}$

$\begin{array}{rcl} 0&=&T_{1}\cos\alpha-T_{2}\sin\alpha\\\Rightarrow\;T_{2}\sin\alpha&=&T_{1}\cos\alpha\\\Rightarrow\;T_{2}&=&\dfrac{T_{1}\cos\alpha}{\sin\alpha}\ ;\\\text{or }T_{1}&=&m'g\sin\alpha\\\Rightarrow\;T_{2}&=&\dfrac{m'g\sin\alpha\cos\alpha}{\sin\alpha}\\\Rightarrow\boxed{T_{2}=m'g\cos\alpha} \end{array}$

2.3 Calcul de leurs valeurs

$\begin{array}{rcl} T_{1}&=&K\left(L-L_{0}\right)\\&=&25(18-16)\cdot10^{-2}\\\Rightarrow\boxed{T_{1}=0.5\,N} \end{array}$

$\begin{array}{rcl} T_{2}&=&\dfrac{T_{1}\cos\alpha}{\sin\alpha}\\&=&\dfrac{0.5\cos60^{\circ}}{\sin60^{\circ}}\\\Rightarrow\boxed{T_{2}=0.29\,N}\end{array}$

3. Déduisons la masse $m'$ de solide $\left(S'\right)$

$\begin{array}{rcl} T_{1}&=&m'g\sin\alpha\\\Rightarrow\;m'&=&\dfrac{T_{1}}{g\sin\alpha}\\&=&\dfrac{0.5} {10\times\sin60^{\circ}}\\\Rightarrow\;m'&=&0.058\,kg\\\Rightarrow\boxed{m'=58\,g } \end{array}$

Commentaires

Anonyme (non vérifié)

sam, 03/19/2022 - 19:19

Vous êtes ici

Solution des exercices : Équilibre d'un solide soumis à des forces - 2nd S

Formulaire de recherche

Exercice 1

Exercice 2

Exercice 3

Exercice 4

Exercice 5

Exercice 6

Exercice 7

Commentaires

Pages

Ajouter un commentaire

Plain text