Solution des exercices : Étude expérimentale des lentilles - 1er s
Classe:
Première
Exercice 1 : Obtention de l'image d'un objet $AB$ par une lentille mince.
Construction de l'image de l'objet AB par la lentille mince
Cas $n^{\circ}1$ :
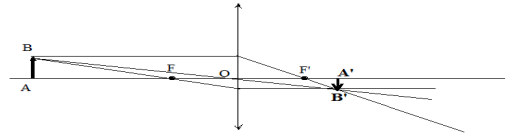
L'image est réelle, inversée(ou renversée) et réduite
Cas $n^{\circ}2$ :
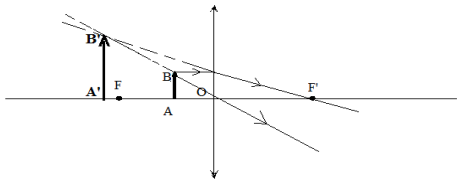
L'image est virtuelle, droite et agrandie
Cas $n^{\circ}3$ :
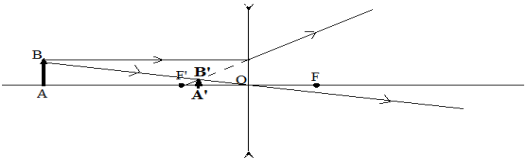
L'image est virtuelle, droite et réduite
Cas $n^{\circ}4$ :
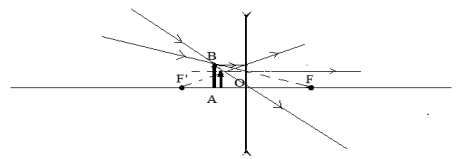
L'image est virtuelle, droite et réduite
Exercice 2
1. Plaçons les points $F$, $F^{\prime}$, $A$ et $B$
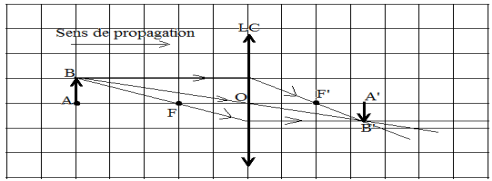
$NB$ : $1$ carreau pour $2\,cm$
2. Calcul de $\overline{OF}$, $\overline{OF}^{\prime}$ et $\overline{OA}$
$\overline{OF}=4.0\,cm$ ;
$\overline{OF}^{\prime}=4.0\,cm$ et
$\overline{OA}=-10.0\,cm$
3. Détermination graphique l'image $A'B'$ de $AB$
$A'B'=1.4\,cm$
Caractérisation de l'image obtenue.
L'image obtenue est réelle, renversée, plus petite que l'objet et à droite du plan focal image
4. Déduction graphique $\overline{OA^{\prime}}$ et $\overline{A'B'}$
$\overline{OA^{\prime}}=6.8\,cm\quad\text{et}\quad\overline{A'B'}=-1.4\,cm$
5. Retrouvons $\overline{OA^{\prime}}$ et $\overline{A'B'}$ en utilisant la formule de conjugaison
$\begin{array}{rcl} \dfrac{1}{\overline{OA'}}-\dfrac{1}{\overline{OA}}&=&\dfrac{1}{\overline{f'}}\\\Rightarrow\dfrac{1}{\overline{OA'}}&=&\dfrac{1}{\overline{f'}}+\dfrac{1}{\overline{OA}}\\\Rightarrow\overline{OA'}&=&\dfrac{\overline{OA}f'}{OA+f'}\\&=&\dfrac{-10\times4}{-10+4}\\\Rightarrow\boxed{\overline{OA'}=6.7\,cm} \end{array}$
$\begin{array}{rcl} \dfrac{\overline{A'B'}}{\overline{AB}}&=&\dfrac{\overline{OA'}}{OA}\\\Rightarrow\overline{A'B'}&=&\dfrac{OA'}{\overline{OA}}\overline{AB}\\&=&\dfrac{6.7}{-10}\times2\\\Rightarrow\boxed{\overline{A'B'}=-1.34\,cm} \end{array}$
6. Calculons le grandissement de l'image
$\begin{array}{rcl} G&=&\dfrac{\overline{A'B'}}{AB}\\&=&\dfrac{-1.4}{2}\\\Rightarrow\boxed{G=-0.7} \end{array}$
Exercice 3
Un objet de grandeur $2.0\,cm$ est placé à $4.0\,cm$ cm d'une loupe, dans un plan perpendiculaire à l'axe principal de celle-ci ; la vergence de cette loupe est $C=20$ dioptries.
1. Calcul de la distance focale de cette loupe
$\begin{array}{rcl} C&=&\dfrac{1}{f}\\\Rightarrow\;f&=&\dfrac{1}{C}\\&=&\dfrac{1}{20}\\\Rightarrow\;f&=&0.05\,m\\\Rightarrow\boxed{f=5\,cm}\end{array}$
2. Construisons l'image de cet objet à travers la loupe à l'échelle $1/2.$
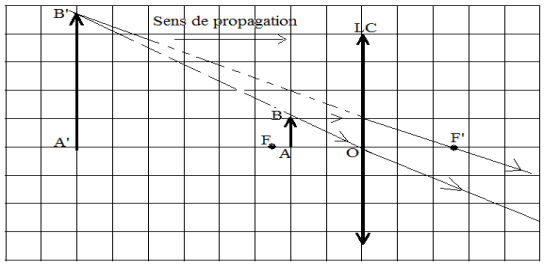
$NB$ : $1\,cm$ pour un carreau
a. Précisons sa nature, réelle ou virtuelle.
L'image est virtuelle
b. Précisons son sens.
L'image est droite, c'est-à-dire même que l'objet
c. Mesurons sa position par rapport à la loupe.
$\begin{array}{rcl} \overline{A'B'}&=&4.8\times 2\\\Rightarrow\boxed{\overline{A'B'}=9.6\,cm} \end{array}$
d. Mesurons sa grandeur
$\overline{A'B'}=4.8\,cm$
Déduisons le rapport de la grandeur de l'image à celle de l'objet
$\begin{array}{rcl} G&=&\dfrac{\overline{A'B'}}{\overline{AB}}\\&=&\dfrac{4.8}{2}\\\Rightarrow\boxed{G=2.4} \end{array}$
Exercice 4
1. Calcul de la vergence de la lentille et donnons son unité.
$\begin{array}{rcl} C&=&\dfrac{1}{f'}\\&=&\dfrac{1}{10\cdot10^{-2}}\\\Rightarrow\boxed{C=10\delta} \end{array}$
L'unité de la vergence est la dioptrie
2. a. Expérience simple pouvant permettre vérifier la distance focale de la lentille.
Pour vérifier la distance focale d'une lentille, il suffit construire l'image nette d'un objet à l'infini.
b. Critère de reconnaissance d'une lentille convergente.
Une lentille convergente est une lentille aux bords plus minces qu'au centre
3.a. Donnons la relation algébrique de Descartes (relation entre les positions de l'objet et de l'image)
La relation entre les positions de l'objet et de l'image est :
$\dfrac{1}{\overline{OA'}}-\dfrac{1}{\overline{OA}}=\dfrac{1}{f^{\prime}}$
b. Précisons les orientations sur un schéma.
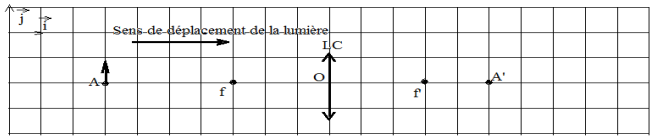
c. Calcul numérique de $\overline{OA}$ et de $\overline{OA^{\prime}}$
$\overline{OA}=16\,cm$
$\begin{array}{rcl} \dfrac{1}{\overline{OA'}}-\dfrac{1}{\overline{OA}}&=&\dfrac{1}{\overline{f'}}\\\Rightarrow\dfrac{1}{\overline{OA'}}&=&\dfrac{1}{\overline{f'}}+\dfrac{1}{\overline{OA}}\\\Rightarrow\overline{OA'}&=&\dfrac{\overline{OA}\cdot f'}{\overline{OA}+f'}\\&=&\dfrac{-16\times10}{-16+10}\\\Rightarrow\boxed{\overline{OA'}=26.7\,cm} \end{array}$
4. L'objet est une petite flèche de hauteur $2.0\,cm$
Donnons la formule de Descartes du grandissement $\gamma$
$\gamma=\dfrac{\overline{OA'}}{\overline{OA}}$
Calcul de $\gamma$
$\begin{array}{rcl} \gamma&=&\dfrac{\overline{OA'}}{\overline{OA}}\\&=&\dfrac{26.7}{16}\\\Rightarrow\boxed{\gamma=-1.7} \end{array}$
Déduisons la taille de l'image $\overline{A'B'}$
$\begin{array}{rcl} \gamma&=&\dfrac{\overline{A'B'}}{\overline{AB}}\\\Rightarrow\overline{A'B'}&=&\gamma\overline{AB}\\&=&-1.7\times2\\\Rightarrow\boxed{\overline{A'B'}=-3.4\,cm} \end{array}$
Exercice 5
1. Calcul :
De la position de l'image $A'B'$ de $AB$ à travers la lentille $L_{1}$
$\begin{array}{rcl} \dfrac{1}{\overline{OA'}}-\dfrac{1}{\overline{OA}}&=&\dfrac{1}{\overline{f'}}\\\Rightarrow\dfrac{1}{\overline{OA'}}&=&\dfrac{1}{\overline{f'}}+\dfrac{1}{OA}\\\Rightarrow\overline{OA'}&=&\dfrac{\overline{OA}\cdot}{\overline{OA}+f}\\&=&\dfrac{-20\times16}{-20+16}\\\Rightarrow\boxed{\overline{OA'}=80\,mm}\end{array}$
$\bullet\ $du grandissement de la lentille $L_{1}$ dans ces conditions.
$\begin{array}{rcl} \gamma&=&\dfrac{\overline{OA'}}{\overline{OA}}\\&=&\dfrac{80}{-20}\\\Rightarrow\boxed{\gamma=-4} \end{array}$
$\bullet\ $la dimension (algébrique) de l'image $A'B'$
$\begin{array}{rcl} \gamma&=&\dfrac{\overline{A'B'}}{\overline{AB}}\\\Rightarrow\overline{A'B'}&=&\gamma\overline{AB}\\&=&-4\times5\\\Rightarrow\boxed{\overline{A'B'}=-20\,mm} \end{array}$
2. L'image $A'B'$ est réelle, renversée par rapport à $AB$
L'image est réelle car l'objet est placé derrière la lentille convergente (Cette image peut être recueillie sur un écran)
L'image est renversée car une lentille convergente donne d'un objet réel, placée derrière le foyer objet, une image renversée
3. Confirmons la position de l'image par une construction.
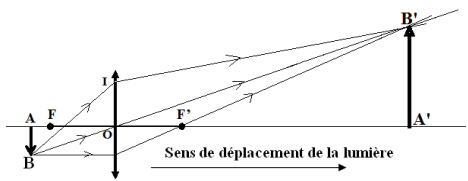
Exercice 6
Détermination, par le calcul, la position, la nature, le sens et la grandeur de l'image
a) L'objet est réel à $2\,m$ de la lentille
$\begin{array}{rcl} \overline{OA'}&=&\dfrac{\overline{OA}\cdot f}{\overline{OA}+f}\\&=&\dfrac{-2\cdot10^{2}\times25}{-2\cdot10^{2}+25}\\\Rightarrow\boxed{\overline{OA'}=28.6\,cm} \end{array}$
L'image est réelle et renversée par rapport à l'objet
Grandeur de l'image
$\begin{array}{rcl} \dfrac{\overline{A'B'}}{\overline{AB}}&=&\dfrac{\overline{OA'}}{\overline{OA}}\overline{AB}\\&=&\dfrac{-100}{-20}\times5\\\Rightarrow\boxed{\overline{A'B'}=25\,cm} \end{array}$
b. L'objet est virtuel et à $15\,cm$ de la lentille
$\begin{array}{rcl} \overline{OA'}&=&\dfrac{\overline{OA'}\cdot f}{OA+f}\\&=&\dfrac{15\times25}{15+25}\\\Rightarrow\boxed{\overline{OA'}=9.4\,cm} \end{array}$
L'image est virtuelle et droite par rapport à l'objet Grandeur de l'image
$\begin{array}{rcl} \overline{A'B'}&=&\dfrac{OA'}{OA}\overline{AB}\\&=&\dfrac{-37.5}{-15}\times5\\\Rightarrow\boxed{\overline{A'B'}=12.5\,cm} \end{array}$
e) L'objet est virtuel et à $1\,cm$ de la lentille
$\begin{array}{rcl} \overline{OA'}&=&\dfrac{\overline{OA}\cdot f}{\overline{OA}+f}\\&=&\dfrac{1\times25}{1+25}\\\Rightarrow\boxed{\overline{OA'}=0.96\,cm} \end{array}$
L'image est virtuelle et droite par rapport à l'objet
Grandeur de l'image
$\begin{array}{rcl} \overline{A'B'}&=&\dfrac{\overline{OA'}}{\overline{OA}}\overline{AB}\\&=&\dfrac{-1.04}{-1}\times5\\\Rightarrow\boxed{\overline{A'B'}=5.2\,cm} \end{array}$
C'est le dans cas $(c)$ on a un fonctionnement en loupe
Exercice 7
1. La distance focale de l'objectif standard
$\begin{array}{rcl} f&=&L\\&=&\sqrt{36^{2}+24^{2}}\\\Rightarrow\boxed{f=43.3\,mm} \end{array}$
Déduisons l'objectif qui convient
La lentille dont la distance focale $f_{2}=50\,cm$ est celui convient
2. Donnons la vergence de cet objectif
$\begin{array}{rcl} C&=&\dfrac{1}{f_{2}}\\&=&\dfrac{1}{50\cdot10^{-3}}\\\Rightarrow\boxed{C=20\delta} \end{array}$
3. Construisons graphiquement l'image $A'B'$ de $AB$
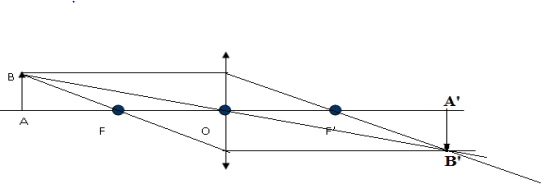
4. Indiquons :
a. La distance de l'image au centre optique
La relation de conjugaison s'écrit :
$\begin{array}{rcl} \dfrac{1}{\overline{O_{1}A^{'}}}-\dfrac{1}{\overline{O_{1}A}}1+1\dfrac{1}{\overline{f'}}\\\Rightarrow\dfrac{1}{\overline{O_{1}A'}}&=&\dfrac{1}{\overline{f'}}+\dfrac{1}{\overline{O_{1}A}}\\\Rightarrow\overline{O_{1}A'}&=&\dfrac{\overline{O_{1}A}\cdot f}{O_{1}A+f}\\&=&\dfrac{-7.5\times50\cdot10^{-3}}{-7.5+50\cdot10^{-3}}\\\Rightarrow\boxed{\overline{O_{1}A'}=5.0\,cm} \end{array}$
b. Le grandissement et la taille de l'image,
$\begin{array}{rcl} G&=&\dfrac{\overline{O_{1}A'}}{\overline{O_{1}A}}\\&=&\dfrac{-5.0}{7.5\cdot10^{2}}\\\Rightarrow\boxed{G=-0.067} \end{array}$
$\begin{array}{rcl} \dfrac{\overline{A'B'}}{\overline{AB}}&=&G\\\Rightarrow\overline{A'B'}&=&G\times\overline{AB}\\&=&-0.067\times1.70\\\Rightarrow\boxed{\overline{A'B'}=-11.6\,cm} \end{array}$
c. Le sens de l'image.
L'image est renversée
Exercice 8
A. Étude graphique
1. Plaçons sur un schéma : la lentille $L$ ; le centre optique O: le foyer objet $F$ ; le foyer image $F'$ et l'objet $AB$
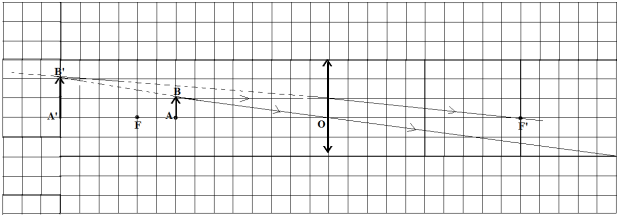
$NB$ : $1\,cm$ pour carreau
2. Construction de l'image $A'B'$ de l'objet $AB$ donnée par la lentille (Voir figure)
3. Détermination graphique :
a. De la hauteur de l'image $\overline{A'B'}$
$\overline{A'B'}=2\,cm$
b. De la position de l'image $\overline{OA'}$
$\overline{OA'}=-14\,cm$
4. Déduisons le grandissement $y$
$\begin{array}{rcl} \gamma&=&\dfrac{\overline{A'B'}}{\overline{AB}}\\&=&\dfrac{2}{1}\\\Rightarrow\boxed{\gamma=2} \end{array}$
B. Étude théorique
On se propose de vérifier par les calculs les résultats précédents
On rappelle les formules suivantes :
$\dfrac{1}{\overline{O_{1}A'}}-\dfrac{1}{\overline{OA}}=\dfrac{1}{\overline{OF'}}$
$\gamma=\dfrac{\overline{OA'}}{\overline{OA}}=\dfrac{\overline{A'B'}}{\overline{AB}}$
1. Calculer $\overline{OA'}$
$\begin{array}{rcl} \overline{O_{1}A'}&=&\dfrac{\overline{O_{1}A}\cdot f}{O_{1}A+f}\\&=&\dfrac{-8\times 10} {-8+10}\\\Rightarrow\boxed{\overline{O_{1}A'}=-40\,cm} \end{array}$
2. Calcul du grandissement $\gamma$
$\begin{array}{rcl}\gamma &=&\dfrac{\overline{OA'}}{OA}\\&=&\dfrac{-40}{-8}\\\Rightarrow\boxed{\gamma =5} \end{array}$
Interpréter le résultat
3. Calculer $\overline{A'B'}$
4. Calcul de la vergence c de la lentille.
$\begin{array}{rcl} C&=&\dfrac{1}{f}\\&=&\dfrac{1}{10\cdot10^{-2}}\\\Rightarrow\boxed{C=10\delta} \end{array}$
Exercice 9
1. Distinction expérimentale puis théorique d'une lentille divergente d'une lentille convergente
Expérimentalement, pour une lentille divergente on peut placer une lentille sur un texte, la soulever et observer :
$\bullet $si les lettres paraissent plus grosses, la lentille est convergente;
$\bullet $si les lettres paraissent plus petites, la lentille est divergente
Théoriquement, si les bords de la lentille sont plus minces que le centre de la lentille, alors c'est une lentille
convergente.
2. Établissons l'expression de la vergence $C$ de la lentille en fonction $\gamma$ de et $x.$
$\begin{array}{rcl} \dfrac{1}{\overline{O_{1}A'}}-\dfrac{1}{\overline{O_{1}A}}&=&\dfrac{1}{\overline{f'}}\\&=&C\ ;\ \\\text{ or }\gamma&=&\dfrac{\overline{O_{1}A'}}{O_{1}A}\\\Rightarrow\overline{O_{1}A'}&=&\gamma\overline{O_{1}A}\\&=&\gamma x\\\Rightarrow\dfrac{1}{yx}-\dfrac{1}{x}&=&C\\\Rightarrow\boxed{C=\dfrac{1}{x}\left(\dfrac{1}{\gamma}-1\right)} \end{array}$
3. Calcul de $C$
$\begin{array}{rcl} C&=&\dfrac{1}{x}(\dfrac{1}{\gamma}-1)\\&=&\dfrac{1}{1.2}(\dfrac{1}{-2}-1)\\\Rightarrow\boxed{C=-1.25\delta} \end{array}$
Déduisons la nature de la lentille.
La vergence est négative, la lentille est une lentille divergente
4. Détermination de la position de l'image $A'B'$ de l'objet $AB$ donnée par la lentille
$\begin{array}{rcl} \overline{O_{1}A'}&=&\gamma\overline{O_{1}A}\\&=&-2\times1.2\\\Rightarrow\boxed{\overline{O_{1}A'}=-2.4\,m} \end{array}$
5. Schéma et construction de l'image $A'B'$ de $AB$
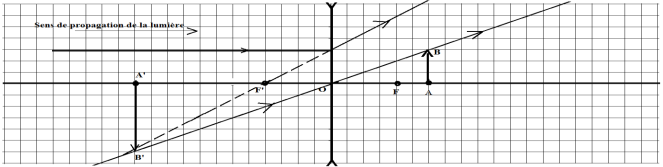

Ajouter un commentaire