Solution des exercices : Classification quantitative des couples oxydant-réducteur ion métalique/métal - 1er s
Classe:
Première
Exercice 1
1. Par convention, le potentiel normal d'oxydo-réduction du couple $H^{+}/H_{2}$ est $0.0V$
2. Pour chaque couple redox, identifions l'oxydant et le réducteur en présentant les résultats sous forme de tableau.
$$\begin{array}{|l|c|c|c|c|} \hline \text{Couple redox}&Ag^{+}/Ag&Cu^{2+}/Cu&Zn^{2+}/Zn&Al^{3+}/Al\\ \hline \text{Oxydant}&Ag^{+}&Cu^{2+}&Zn^{2+}&Al^{3+}\\ \hline \text{Réducteur}&Ag&Cu&Zn&Al\\ \hline \end{array}$$
3. Demi-équation de réduction pour chacun des couples redox
$Ag\ \longrightarrow\ Ag^{+}\ +\ e$
$Cu\ \longrightarrow\ Cu^{2+}\ +\ 2e$
$Fe\ \longrightarrow\ Fe^{2+}\ +\ 2e$
$Al\ \longrightarrow\ Al^{3+}\ +\ 3e$
4.Couples de réactifs qui donnent lieu à une réaction spontanée sont :
$Ag^{+}+Zn$,
$Cu+Ag^{+}$,
$Al+Cu^{2+}$
et $Zn+H^{+}$
Équations d'oxydoréduction correspondante.
$\begin{array}{lc} Zn\ \longrightarrow\ Zn^{2+}\ +\ 2e&\\&\Rightarrow\;Zn\ +\ 2Ag^{+}\ \longrightarrow\ Zn^{2+}\ +\ 2Ag\\2\left(Ag^{+}\ +\ e\ \longrightarrow\ Ag\right)& \end{array}$
$\begin{array}{lc} Cu\ \longrightarrow\ Cu^{2+}\ +\ 2e&\\&\Rightarrow\;Cu\ +\ 2Ag^{+}\ \longrightarrow\ Cu^{2+}\ +\ 2Ag\\2\left(Ag^{+}\ +\ e\ \longrightarrow\ Ag\right)& \end{array}$
$\begin{array}{lc} 3\left(Cu^{2+}\ 2e\ \longrightarrow\ Cu\right)&\\&\Rightarrow\;Cu^{2+}\ +\ 2Al\ \longrightarrow\ 3Cu\ +\ 2Al^{3+}\\2\left(Ag\ \longrightarrow\ Al^{3+}\ +\ 3e\right)& \end{array}$
$\begin{array}{lc} 2\left(H^{+}\ +\ e\ \longrightarrow\ \dfrac{1}{2}H_{2}\right)&\\&\Rightarrow\;2H^{+}\ +\ Zn\ \longrightarrow\ H_{2}\ +\ 2Zn^{2+}\\Zn\ \longrightarrow\ Zn^{2+}\ +\ 2e& \end{array}$
5. Détermination de, dans chaque cas, l'anode et la cathode.
$$\begin{array}{|l|c|c|c|c|} \hline \text{Pile}&Zn|Zn^{2+}\ ||\ Ag^{+}|Ag&Cu|Cu^{2+}\ ||\ Ag^{+}|Ag&Al|Al^{3+}\ ||\ Cu^{2+}|Cu&Zn|Zn^{2+}\ ||\ H^{+}|H_{2}\\ \hline \text{Anode}&Zn|Zn^{2+}&Cu|Cu^{2+}&Al|Al^{3+}&Zn|Zn^{2+}\\ \hline \text{Cathode}&Ag|Ag^{+}&Ag|Ag^{+}&Cu|Cu^{2+}&H^{+}|H_{2}\\ \hline E&1.56V&0.46V&2.0V&0.76V\\\hline \end{array}$$
Calcul de la force électromotrice de chaque pile
$\begin{array}{rcl} E_{Zn|Zn^{2+}\ ||\ Ag^{+}|Ag}&=&E_{Ag|Ag^{+}}-E_{Zn|Zn^{+}}\\&=&0.8-(-0.76)\\\Rightarrow\;E_{Zn|Zn^{2+}\ ||\ Ag^{+}|Ag}&=&1.56V \end{array}$
$\begin{array}{rcl} E_{Cu|Cu^{2+}\ ||\ Ag^{+}|Ag}&=&E_{Ag|Ag^{+}}-E_{Cu|Cu^{2+}}\\&=&0.8-0.34\\\Rightarrow\;E_{Cu|Cu^{2+}\ ||\ Ag^{+}|Ag}&=&0.46V \end{array}$
$\begin{array}{rcl} E_{Al|Al^{3+}\ ||\ Cu^{2+}|Cu}&=&E_{Cu|Cu^{2+}}-E_{Al|Al^{3+}}\\&=&0.34-(-1.66)\\\Rightarrow\;E_{Al|Al^{3+}\ ||\ Cu^{2+}|Cu}&=&2.0V \end{array}$
$\begin{array}{rcl} E_{Zn|Zn^{2+}\ ||\ Ag^{+}|Ag}&=&E_{H^{+}|H_{2}}-E_{Zn|Zn^{+}}\\&=&0.0-(-0.76)\\\Rightarrow\;E_{Zn|Zn^{2+}\ ||\ H^{+}|H_{2}}&=&0.76V \end{array}$
Exercice 2
1.1. Demi-équations des couples redox en présence.
$Fe^{2+}\ +\ 2e\ \longrightarrow\ Fe$
$Zn\ \longrightarrow\ Zn^{2+}\ +\ 2e$
Précisons le sens dans lequel chaque réaction a effectivement lieu lorsque la pile débite.
A l'anode, le zinc s'oxyde
A la cathode l'ion $Fe^{2+}$ est réduit
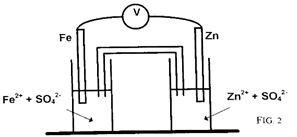
1.2 Précisons la polarité de la pile ; c'est-à-dire le signe $+$ ou $-$ de chacune des électrodes
La tige de fer trempant dans une solution aqueuse de sulfate de fer $(Il)$ constitue la borne positive $(+)$ de la pile.
La tige de zinc trempant dans une solution aqueuse de sulfate de zinc (Il constitue la borne négative $(-)$ de la pile
2.1 Le zinc empêche la corrosion du fer parce que c'est lui, possédant le potentiel éléctrochimique le plus bas d'après la classification électrochimique, qui s'oxyde à la place du zinc
Le zinc (métal plus réducteur), a un potentiel électrochimique moins élevé que celui du métal à protéger(fer).
La protection reste efficace tant que le revêtement par le zinc n'est pas totalement détruit et même si, à la suite d'un choc par exemple, la couche de zinc est interrompue.
2.2 A la place du zinc, si on dépose de la même manière une couche de chrome sur une tôle de fer, le chrome empêche la corrosion du fer puisque c'est lui est attaqué à la place du fer
La protection reste efficace tant que le chrome n'est pas totalement détruit ;
2.3 Le nickel(métal moins réducteur), a un potentiel électrochimique plus élevé que celui du métal à protéger(fer) et la protection n'est plus efficace.
Il se forme une pile de corrosion, le métal à protéger (fer) est oxydé
Exercice 3
1. Montrons que le cuivre est attaqué
Le potentiel électrochimique du couple $Au^{3+}/Au$ $\left(E_{1}=1.5V\right)$ est plus élevé que celui du couple $Cu^{2+}/Cu$
L'oxydant $Au^{3+}$ du couple $Au^{3+}/Au$ va donc réagir avec le réducteur $Cu$ du couple $Cu^{2+}/Cu$
2. Équation-bilan de cette réaction chimique.
$\begin{array}{lc} 3\left(Cu\ \longrightarrow\ Cu^{2+}\ +\ 2e\right)&\\&\Rightarrow\;3Cu\ +\ 2Au^{3+}\ \longrightarrow\ 3Cu^{2+}\ +\ 2Au\\2\left(Au^{3+}\ +\ 3e\ \longrightarrow\ Au\right)& \end{array}$
3. Détermination du nombre de moles initial $n_{1}$ de moles de cuivre.
$\begin{array}{rcl} n_{1}&=&\dfrac{m}{M}\\&=&\dfrac{50\cdot 10^{-3}}{63.5}\\\Rightarrow\;n_{1}&=&0.79\cdot 10^{-3}mol \end{array}$
4. Détermination du nombre de moles initial $n_{2}$ d'ions $Au^{3+}$ présents dans la solution de chlorure d'or.
$\begin{array}{rcl} n_{2}&=&c\times V\\&=&10^{-2}\times 100\cdot 10^{-3}\\\Rightarrow\;n_{2}&=&10^{-3}mol \end{array}$
5. Détermination du réactif introduit en excès
$\begin{array}{lc} \dfrac{n_{1}}{3}=\dfrac{0.79\cdot 10^{-3}}{3}=0.26\cdot 10^{-3}mol&\\&\Rightarrow\dfrac{n_{2}}{2}\succ\dfrac{n_{1}}{3}\\\dfrac{n_{2}}{2}=\dfrac{10^{-3}}{2}=0.5\cdot 10^{-3}mol& \end{array}$
La solution de chlorure d'or $\left(AuCl_{3}\right)$ est le réactif introduit en excès
Exercice 4
1. Calcul du temps $t$ nécessaire à l'opération.
$\begin{array}{rcl} \dfrac{It}{Ne}&=&\dfrac{m}{M}\\\Rightarrow\;t&=&\dfrac{mNe}{MI}\\&=&\dfrac{1.875\times 6.02\cdot 10^{23}\times 1.6\cdot 10^{-19}}{108\times 2}\\\Rightarrow\;t&=&836s \end{array}$
2.1. Entre les deux éléments métalliques entrant dans la constitution de la statue est celui qui possède le plus grand pouvoir réducteur est le fer.
2.2. Équation bilan de l'oxydoréduction de ces deux éléments.
$\begin{array}{lc} Cu^{2+}\ +\ 2e\ \longrightarrow\ Cu&\\&\Rightarrow\;Cu^{2+}\ +\ Fe\ \longrightarrow\ Cu\ +\ Fe^{2+}\\Fe\ \longrightarrow\ Fe^{2+}\ +\ 2e& \end{array}$
2.2. a) Le cuivre est le métal constituant l'électrode positive de cette pile.
b) Précisons et justifions le sens de circulation des électrons dans le circuit.

Le courant circule de la borne positive de la pile vers la borne négative.
3. Le zinc métal, étant plus réducteur que le fer, s'oxyde à la place du fer et protège le fer.
Équation de la réaction d'oxydoréduction correspondante.
$\begin{array}{lc} Cu^{2+}\ +\ 2e\ \longrightarrow\ Cu&\\&\Rightarrow\;Cu^{2+}\ +\ Zn\ \longrightarrow\ Cu\ +\ Zn^{2+}\\Zn\ \longrightarrow\ Zn^{2+}\ +\ 2e& \end{array}$
Exercice 5
1.1. Indiquons la polarité des électrodes.
Le courant circule dans un circuit extérieur de l'électrode de nickel vers l'électrode de fer.
L'électrode de nickel constitue donc la borne positive, l'électrode du fer est borne négative.
Équation de la réaction spontanée, qui se produit dans la pile $P_{1}.$
$\begin{array}{lc} Ni^{2+}\ +\ 2e\ \longrightarrow\ Ni&\\&\Rightarrow\;Ni^{2+}\ +\ Fe\ \longrightarrow\ Ni\ +\ Fe^{2+}\\Fe\ \longrightarrow\ Fe^{2+}\ +\ 2e& \end{array}$
1.2. Montrons que le potentiel normal du couple $Fe^{2+}/Fe$ est inférieur à une valeur que l'on déterminera.
$\begin{array}{rcl} E^{\circ}&=&E^{\circ}_{\left(Ni^{2+}/Ni\right)}-E^{\circ}_{\left(Fe^{2+}/Fe\right)}\\&=&-0.25-E^{\circ}\left(Fe^{2+}/Fe\right) \end{array}$
$\begin{array}{rcl} E^{\circ}&\succ &0\\\Rightarrow-0.25-E^{\circ}_{\left(Fe^{2+}/Fe\right)}&\succ&0\\\Rightarrow\;E^{\circ}_{\left(Fe^{2+}/Fe\right)}&\prec&-0.25 \end{array}$
Déduisons si le fer est attaqué par une solution d'acide ou non.
Le fer est attaqué car son potentiel est plus faible que celui du potentiel du couple $H^{+}//H_{2}$
2.1. Comparons les potentiels normaux des couples $Fe^{2+}/Fe$ et $Zn^{2+}/Zn.$
L'oxydant $Fe^{2+}$ du couple $Fe^{2+}/Fe$ réagit le $Zn$ du couple $Zn^{2+}/Zn$ pour donner le dépôt.
Le couple $Fe^{2+}/Fe$ a donc le potentiel électrochimique le plus élevé que celui du couple $Zn^{2+}/Zn$
2.2. Le couple a donc le potentiel électrochimique le plus élevé que celui du couple $Pb^{2+}/Pb$
On observe une réaction chimique quand on plonge une lame de fer dans une solution contenant des ions $Pb^{2+}$, car l'oxydant $Pb^{2+}$ du couple $Pb^{2+}/Pb$ réagit le réducteur $Fe$ du couple $Fe^{2+}/Fe$
3.1. Symbole de la pile $P_{2}$
$Fe|Fe^{2+}\ ||\ Zn^{2+}|Zn$
Équation chimique associé à la pile.
$\begin{array}{lc} Fe^{2+}\ +\ 2e\ \longrightarrow\ Fe&\\&\Rightarrow\;Zn\ +\ Fe^{2+}\ \longrightarrow\ Zn^{2+}\ +\ Fe\\Zn\ \longrightarrow\ Zn^{2+}\ +\ 2e& \end{array}$
3.2. Calcul de $E^{\circ}_{\left(Fe^{2+}/Fe\right)}$
$\begin{array}{rcl} E_{2}&=&E_{Fe|Fe^{2+}}-E_{Zn|Zn^{2+}}\\\Rightarrow\;E_{Fe|Fe^{2+}}&=&E_{2}+E_{Zn|Zn^{2+}}\\&=&0.32-0.76\\\Rightarrow\;E_{Fe|Fe^{2+}}&=&-0.44V \end{array}$
Exercice 6
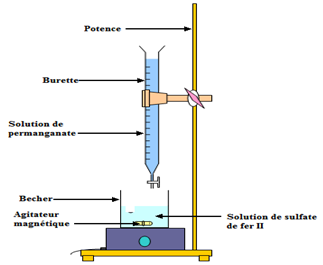
1) Schéma annoté du dispositif.

La solution dosant est le permanganate de potassium $KMnO_{4}$ et l'espèce à doser est la solution de sulfate de fer $II$
Précisons le rôle de $H_{2}$ $SO_{4}$
Il sert à transformer l'ion permanganate $MnO_{4}^{-}$ en ion manganeux $Mn^{2+}$
2) a) Équation de la réaction redox qui a lieu lors du dosage
$\begin{array}{lc} MnO_{4}^{-}\ +\ 8H^{+}\ +\ 5e\ \longrightarrow\ Mn^{2+}\ +\ 4H_{2}O&\\&\Rightarrow\;MnO_{4}^{-}\ +\ 8H^{+}\ +\ 5Fe^{2+}\ \longrightarrow\ Mn^{2+}\ +\ 4H_{2}O\ +\ 5Fe^{3+}\\5\left(Fe^{2+}\ \longrightarrow\ Fe^{3+}\ +\ e\right)& \end{array}$
b) A l'équivalence redox, le volume de la solution dosant est $V_{2}=20mL.$
c) On peut reconnaître l'équivalence redox par la disparition de la coloration verte caractéristique des ions $Fe^{2+}$
d) Détermination de la valeur de $C_{1}$
A l'équivalence :
$\begin{array}{rcl} \dfrac{n_{1}}{5}&=&\dfrac{n_{2}}{1}\\\Rightarrow\dfrac{C_{1}V_{1}}{5}&=&\dfrac{C_{2}V_{2}}{1}\\\Rightarrow\;C_{1}&=&\dfrac{5C_{2}V_{2}}{V_{1}}\\&=&\dfrac{5\times 0.01\times 20}{10}\\\Rightarrow\;C_{1}&=&0.1mol\cdot L^{-1} \end{array}$
II.
1) Le symbole de ce schéma de pile
$Cu|Cu^{2+}\ ||\ Fe^{2+}|Fe$
Équation chimique associée.
$\begin{array}{lc} Cu^{2+}\ +\ 2e\ \longrightarrow\ Cu&\\&\Rightarrow\;Fe\ +\ Cu^{2+}\ \longrightarrow\ Fe^{2+}\ +\ Cu\\Fe\ \longrightarrow\ Fe^{2+}\ +\ 2e& \end{array}$
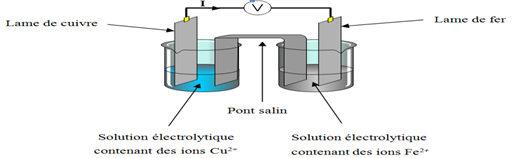
2) a) Détermination de la polarité des bornes de la pile.
La demi-pile formée de la solution $\left(S_{1}\right)$ dans laquelle on plonge une lame de fer constitue la borne négative
La demi-pile formée par une solution de d'ions $Cu^{2+}$ dans laquelle on plonge une lame de cuivre est la borne positive.
b) Écriture de la transformation chimique qui se produit dans chaque compartiment de la pile.
$Cu^{2+}\ +\ 2e\ \longrightarrow\ Cu$
$Fe\ \longrightarrow\ Fe^{2+}\ +\ 2e$
Équation bilan de la réaction chimique spontanée quand la pile débite un courant.
$Fe\ +\ Cu^{2+}\ \longrightarrow\ Fe^{2+}\ +\ Cu$
c) Précisons le rôle du pont salin
Le rôle du pont salin permet de fermer le circuit et d'assurer le passage du courant.
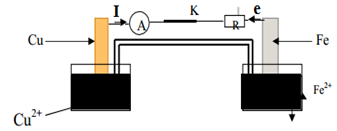
d) Schéma de la figure 1 $(K$ fermé$)$ en précisant le sens du courant et des électrons dans le circuit.

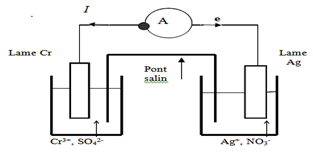
Exercice 7 : Pile chrome argent
1. Définition du potentiel standard d'un couple oxydant-réducteur.
Le potentiel standard d'un couple $M^{n+}/M$ est la différence de potentiel entre le potentiel rédox du couple $M^{n+}/M$ et le potentiel rédox du couple $H^{+}/H_{2}$ dans des conditions standard c'est-à-dire $P\left(H_{2}\right)=1atm$ et $pH=1$
Calcul de la f.é.m. de cette pile.
$\begin{array}{rcl} E^{\circ}&=&E^{\circ}\left(Ag^{+}/Ag\right)-E^{\circ}\left(Cr^{3+}/Cr\right)\\&=&0.80-(-0.74V)\\\Rightarrow\;E^{\circ}&=&1.54V \end{array}$
2. Schéma de la pile en justifiant les polarités des électrodes.

Les électrons sont les charges qui circulent à l'intérieur et à l'extérieur de la pile, lorsque celle-ci débite.
Indiquons leur sens de déplacement sur le schéma (voir schéma)
3. équations-bilans des réactions qui ont lieu dans chaque demi-pile
$Cr\ \longrightarrow\ Cr^{3+}\ +\ 3e$
$3\left(Ag^{+}\ +\ e\ \longrightarrow\ Ag\right)$
Équation du bilan de la réaction chimique.
$Cr\ +\ 3Ag^{+}\ \longrightarrow\ Cr^{3+}\ +\ 3Ag$
4. Au cours du fonctionnement de la pile, la masse d'une des électrodes diminue de $80.2mg.$
4.1. L'électrode dont la masse d'une des électrodes diminue est l'électrode de chrome.
4.2. Calcul de la variation de masse de l'électrode d'argent
$\begin{array}{rcl} \dfrac{n_{Ag}}{3}&=&n_{Cr}\\\Rightarrow\dfrac{m_{Ag}}{3M_{Ag}}&=&\dfrac{m_{Cr}}{M_{Cr}}\\\Rightarrow\;m_{Ag}&=&\dfrac{m_{Cr}\times 3M_{Ag}}{M_{Cr}}\\\Rightarrow\;m_{Ag}&=&\dfrac{80.2\cdot 10^{-3}\times 108}{52}\\\Rightarrow\;m_{Ag}&=&0.50g \end{array}$
4.3. Concentration $C_{1}$ en ion $Ag^{+}$
$\begin{array}{rcl} C_{1}&=&\left(0.01\times 100\cdot 10^{-3}+\dfrac{0.50}{108}\right)\dfrac{1}{200\cdot 10^{-3}}\\\Rightarrow\;C_{1}&=&0.028mol\cdot L^{-1} \end{array}$
4.4. Concentration $C_{2}$ en ion $Cr^{3+}$
$\begin{array}{rcl} C_{2}&=&\left(0.01\times 100\cdot 10^{-3}-\dfrac{80.2\cdot 10^{-3}}{52}\right)\dfrac{1}{200\cdot 10^{-3}}\\\Rightarrow\;C_{2}&=&0.0027mol\cdot L^{-1} \end{array}$
Exercice 8
A. Action des pluies acides sur le zinc
1.1. Le pôle $(-)$ correspond au métal du couple de plus bas potentiel ; c'est donc la lame de zinc $(Zn)$
1.2. Valeur de la force électromotrice E attendue pour cette pile.
$E=0.00-(-0.76)=0.76V$
2. Il y a oxydation à la borne négative $(-)$ de la pile
3. Équation globale de la réaction de fonctionnement de cette pile.
$\begin{array}{lc} 2\left(H^{+}\ +\ e\ \longrightarrow\ \dfrac{1}{2}H_{2}\right)&\\&\Rightarrow\;2H^{+}\ +\ Zn\ \longrightarrow\ H_{2}\ +\ Zn^{2+}\\ Zn\ \longrightarrow\ Zn^{2+}\ +\ 2e& \end{array}$
B. Action des pluies acides sur le cuivre
l. Valeur de la force électromotrice E attendue pour cette pile.
$E=0.34-0.00=0.34V$
2. Il y a réduction à la borne positive $(+)$ de la pile
3. Équation globale de la réaction de fonctionnement de cette pile.
$\begin{array}{lc} 2\left(\dfrac{1}{2}H_{2}\ +\ H_{2}O\ \longrightarrow\ H_{3}O^{+}\ +\ e\right)&\\&\Rightarrow\;H_{2}\ +\ 2H_{2}O\ +\ Cu^{2+}\ \longrightarrow\ 2H_{3}O^{+}\ +\ Cu\\ Cu^{2+}\ +\ 2e\ \longrightarrow\ Cu& \end{array}$
C. Conclusion
l. Le gaz dégagé qui explose dans l'air à la moindre étincelle lorsque l'on plonge le zinc dans une solution acide est le dihydrogène.
2. Indépendamment du coût, la gouttière en cuivre sera préférée à la gouttière en zinc dans les régions où les pluies acides sont fréquentes parce que ce métal ayant le potentiel le plus élevé ne peut être oxydé par l'ion $H^{+}$ des pluies acides.
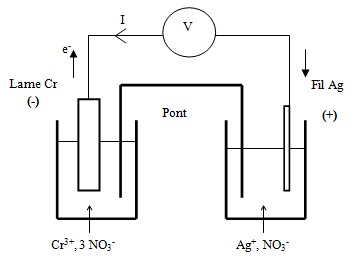
Exercice 9 : Pile chrome-argent
$\begin{array}{rcl} n_{e}&=&n\quad\text{or}\quad n_{e}F&=&It\\\Rightarrow\;n&=&\dfrac{It}{F}\\&=&\dfrac{0.80\times 21.0\times 60}{96500}\\\Rightarrow\;n&=&0.0104mol \end{array}$
a) Le pôle $(+)$ correspond au métal du couple de plus haut potentiel ; c'est donc le fil $d'Ag.$
Le pôle $(-)$ est donc la lame de $Cr.$
Le courant va du pôle $(+)$ vers le pôle $(-)$ et les $e^{-}$ en sens contraire.

b) Calcul de la f.é.m. de cette pile
$\begin{array}{rcl} E_{Ag}-Cr&=&E_{0}\left(Ag^{+}/Ag\right)-E_{0}\left(Cr^{3+}/Cr\right)\\&=&0.80-(-0.74)\\E_{Ag}-Cr&=&1.54V \end{array}$
c) La réaction qui se produit dans la pile est la réaction rédox naturelle entre l'oxydant le plus fort $\left(Ag^{+}\right)$ et le réducteur le plus fort $(Cr)$ soit :
$3Ag^{+}\ +\ Cr\ \longrightarrow\ 3Ag^{+}\ +\ Cr^{3+}$
d) Calcul de la masse minimale de la lame de chrome pour que les ions argent soient entièrement consommés.
$\begin{array}{rcl} n_{0}\left(Ag^{+}\right)&=&C_{0}V_{\text{sol}}\\&=&C_{0}V_{2}\\&=&1.00\times 0.250\\&=&0.250mol \end{array}$
D'après l'équation bilan
$n_{0}(Cr)=\dfrac{1}{3}n_{0}\left(Ag^{+}\right)$
$\begin{array}{rcl} m_{0}(Cr)&=&n_{0}(Cr)M(Cr)\\&=&\dfrac{1}{3}C_{0}V_{2}M(Cr)\\&=&4.33g \end{array}$
Pour $m(Cr)>m_{0}(Cr)$, $Cr$ est en excès et les ions $Ag^{+}$ sont entièrement consommés
e) Calcul de la concentration des ions chrome $(III)$ et l'augmentation de la masse de l'électrode d'argent.
D'après l'équation bilan :
$\begin{array}{rcl} n\left(Cr^{3+}\right)_{\text{Obtenu}}&=&\dfrac{1}{3}n_{0}\left(Ag^{+}\right)\\&=&\dfrac{1}{3}C_{0}V_{2}\\\text{Donc}\quad n\left(Cr^{3+}\right)_{\text{Final}}&=&n\left(Cr^{3+}\right)_{\text{initial}}+n\left(Cr^{3+}\right)_{\text{Obtenu}}\\&=&C_{0}V_{1}+\dfrac{1}{3}C_{0}V_{2}\\&=&\dfrac{4}{3}C_{0}V\\\text{Car}\quad V_{1}=V_{2}&=&V\\\text{D'où on tire}\quad c\left(Cr^{3+}\right)_{\text{final}}&=&n\left(Cr^{3+}\right)_{\text{final}}/V\\&=&\dfrac{4}{3}C_{0}V/V\\&=&\dfrac{4}{3}C_{0}\\&=&1.33mol\cdot L^{-1} \end{array}$
D'après l'équation bilan :
$\begin{array}{rcl} n(Ag)&=&n\left(Ag^{+}\right)\\&=&n_{0}\left(Ag^{+}\right) \end{array}$
$\begin{array}{rcl} m(Ag)&=&n(Ag)M(Ag)\\&=&C_{0}VM(Ag)\\&=&27.0g \end{array}$

Ajouter un commentaire