Solution des exercices : Dipôles Passifs - 1er s
Classe:
Première
Exercice 1
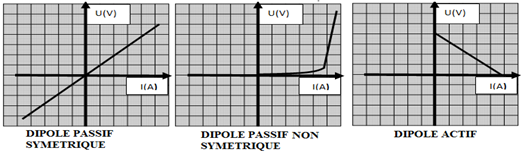
1. Représentation de l'allure de la caractéristique intensité-tension dipôlesd'une dipôle :
$f$ dipôle symétrique passif.
$g$ dipôle asymétrique passif
$h$ dipôle actif.
2. Variation de la résistance d'un fil conducteur :
$R=\rho\dfrac{1}{S}$
2.1. La résistance d'un fil conducteur diminue avec sa section $S$
2.2. La résistance d'un fil conducteur augmente avec sa longueur $1$
Exercice 2
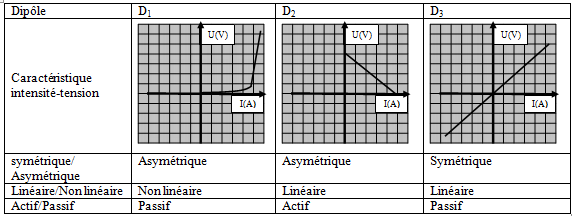
Complétons le tableau suivant.
Exercice 3
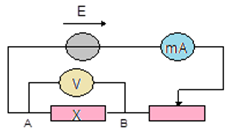
1. La résistance $X$ du conducteur ohmique placé entre $A$ et $B$
$\begin{array}{rcl} X&=&\dfrac{U}{I}\\&=&\dfrac{3.29}{7.13\cdot 10^{-3}}\\ \Rightarrow\;X&=&461\Omega \end{array}$
2. Indication de l'ampèremètre
$\begin{array}{rcl} I&=&\dfrac{U}{X}\\&=&\dfrac{2.03}{461}\\ \Rightarrow\;I&=&4.40\;,mA \end{array}$
3. Indication affichée par le voltmètre
$\begin{array}{rcl} U&=&XI\\&=&461\times5.12\cdot10^{-3}\\ \Rightarrow\;U&=&2.36V \end{array}$
Exercice 4
$$\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|c|} \hline U(V)&0.05&0.1&0.3&0.4&0.6&0.8&2&3&4&5&6&7\\ \hline I(mA)&25&50&100&111&129&148&240&295&345&395&435&475\\ \hline \end{array}$$
1. Traçons la caractéristique intensité tension de la lampe.
2. Détermination, pour chaque point de fonctionnement la résistance $R$ de la lampe.
$$\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|c|} \hline U(V)&0.05&0.1&0.3&0.4&0.6&0.8&2&3&4&5&6&7\\ \hline I(mA)&25&50&100&111&129&148&240&295&345&395&435&475\\ \hline R&2&2&3&3.6&4.7&5.4&8.3&10&11.6&12.7&13.8&14.7\\ \hline U\cdot I&1.25&5&30&44.4&77.4&118.4&480&885&1380&1975&2610&3325\\ \hline \end{array}$$
Représentation graphique de la relation $R=f(U\cdot I).$
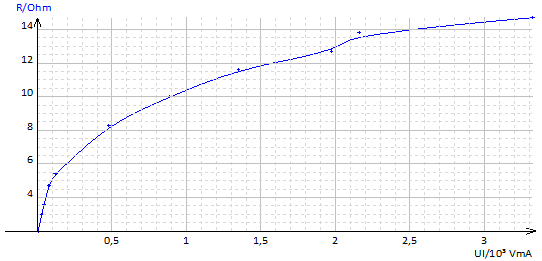
La variation de la résistance $R$ du filament avec la température est croissante.
3. Détermination de la relation affine qui décrit approximativement le fonctionnement de la lampe dans ce domaine d'utilisation.
$U=aI+b\Rightarrow\left\lbrace\begin{array}{lcl} 3&=&295\cdot10^{-3}a+b\quad(1)\\ 7&=&475\cdot10^{-3}a+b\quad(2) \end{array}\right.$
$\begin{array}{rcl} (2)-(1)\Rightarrow\;4&=&180\cdot10^{-3}a\\ \Rightarrow\;a&=&\dfrac{4}{180\cdot10^{-3}}\\\\ \Rightarrow\;a&=&22.2V\cdot A^{-1} \end{array}$
$\begin{array}{rcl} (1)\Rightarrow\;b&=&3-295\cdot10^{-3}\times22.2\\ \Rightarrow\;b&=&-3.55V\\ \Rightarrow\;U&=&22.2I-3.55 \end{array}$
Exercice 5
1. Représentation du schéma du montage qui permet de tracer cette caractéristique.
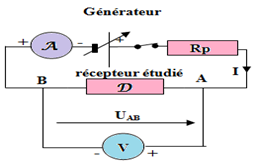
2. Précisons la nature du dipôle étudié.
La caractéristique du dipôle est une fonction linéaire.
Le dipôle est donc un résistor ou un conducteur ohmique.
Déterminons sa résistance
$\begin{array}{rcl} R&=&\dfrac{\Delta U}{\Delta I} \\&=&\dfrac{2.5}{1.5\cdot10^{3}}\\\Rightarrow\;R&=&1.7\cdot 10^{-3}\Omega \end{array}$
Exercice 6
On réalise un circuit électrique simple avec une pile dont la tension entre ses bornes est $U=12V$ et un résistor de résistance $R=100\Omega$ qui supporte une intensité maximale de $100mA.$
1. Vérifions si on ne risque pas d'endommager $R$ et justifions
$\begin{array}{rcl} I&=&\dfrac{U}{R} \\&=&\dfrac{12}{100}\\ \Rightarrow\;I&=&120mA \end{array}$
$I\succ I_{\text{max}}$ ; l'intensité qui traverse le résistor est supérieure à l'intensité maximale supportable.
On risque donc d'endommager le résistor de résistance $R$
2. Résistance minimale $R'$ qu'il faut mettre en série avec $R$
$\begin{array}{rcl} U&=&\left(R+R^{\prime}\right)I\\ \Rightarrow\;R+R^{\prime}&=&\dfrac{U}{I}\\ \Rightarrow\;R^{\prime}&=&\dfrac{U}{I}-R\\&=&\dfrac{12}{100\cdot10^{-3}}-100\\ \Rightarrow\;R^{\prime}&=&20\Omega \end{array}$
3.1 Détermination de la valeur de $R"$ pour que l'intensité du courant soit égale à $0.12A$
$\begin{array}{rcl} \left(\dfrac{RR"}{R+R"}+R'\right)I&=&U\\\Rightarrow\dfrac{RR"}{R+R"}+R'&=&\dfrac{U}{I}\\\Rightarrow\dfrac{RR"}{R+R"}&=&\dfrac{U}{I}-R'\\&=&\dfrac{12}{0.12}-20\\&=&80\\\Rightarrow\dfrac{RR"}{R+R"}&=&80\\\Rightarrow\dfrac{100R"}{100+R"}&=&80\\\Rightarrow\;80(100+R")&=&100R"\\\Rightarrow\;100R"-80R"&=&80\times100\\\Rightarrow\;R"&=&\dfrac{80\times 100}{20}\\\Rightarrow\;R"&=&400\Omega \end{array}$
3.2 Détermination de l'intensité du courant qui traverse $R'$, $I=0.12A$
Déduisons celui qui traverse $R$
$\begin{array}{rcl} U_{R}&=&U-U_{R'}\\ \Rightarrow\;RI_{1}&=&U-R'I\\ \Rightarrow\;I_{1}&=&\dfrac{U-R'I}{R}\\&=&\dfrac{12-20\times 0.12}{100}\\ \Rightarrow\;I_{1}&=&96mA \end{array}$
Exercice 7
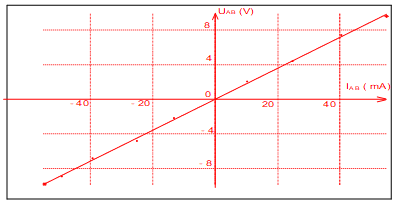
1. Expliquons pourquoi l'observation de ce graphe permet d'affirmer que le dipôle $AB$ est un conducteur ohmique.
Un dipôle $AB$ est un conducteur ohmique (résistor) sa caractéristique courant/tension est une fonction linéaire, c'est à dire une droite passant par l'origine
Le graphe est une droite linéaire caractéristique d'un conducteur ohmique.
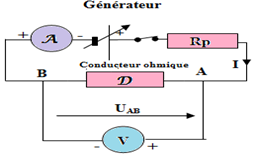
2. Schéma conventionnel du dipôle $AB$
3. Calcul de la résistance du conducteur ohmique à partir de sa caractéristique.
$\begin{array}{rcl} R&=&\dfrac{\Delta U}{\Delta I}\\&=&\dfrac{7.5-0}{(40-0)\cdot10^{-3}}\\ \Rightarrow\;R&=&187.5\Omega \end{array}$
4.1. La tension aux bornes du conducteur ohmique lorsqu'il est traversé par un courant de $15\,mA$
$\begin{array}{rcl} U&=&RI\\&=&187.5\times15\cdot10^{-3}\\ \Rightarrow\;U&=&2.8V \end{array}$
4.2 L'intensité du courant qui traverse le conducteur ohmique lorsqu'il est soumis à une tension de $4V$
$\begin{array}{rcl} I&=&\dfrac{U}{R}\\&=&\dfrac{4}{187.5}\\ \Rightarrow\;I&=&21.3mA \end{array}$
5. L'intensité maximale que peut supporter le composant
$\begin{array}{rcl} I&=&\dfrac{U}{R}\\&=&\dfrac{10}{187.5}\\ \Rightarrow;I&=&53.3mA \end{array}$
Exercice 8
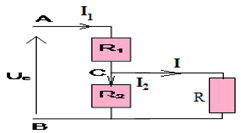
1.1 Exprimons en fonction de $U_{e}$, $R_{1}$ et $R_{2}$ l'intensité $I$ du courant qui circule dans le circuit.
$U_{e}=\left(R_{1}+R_{2}\right)I$
1.2 Déduisons l'expression de la tension de sortie $U_{s}$ en fonction de $U_{e}$, $R_{1}$ et $R_{2}$
$\begin{array}{rcl} \left\lbrace\begin{array}{lcl} U_{e}&=&\left(R_{1}+R_{2}\right)I\\ U_{s}&=&R_{2}I \end{array}\right.\\ \Rightarrow\dfrac{U_{s}}{U_{e}}&=&\dfrac{R_{2}}{R_{1}+R_{2}} \\\Rightarrow\;U_{s}&=&\dfrac{R_{2}}{R_{1}+R_{2}}U_{e} \end{array}$
1.3. Calcul des valeurs $I$ et de $U_{S}$
$\begin{array}{rcl} U_{e}&=&\left(R_{1}+R_{2}\right)I\\ \Rightarrow;I&=&\dfrac{U_{e}}{R_{1}+R_{2}}\\&=&\dfrac{6.0}{(2.2+4.7)\cdot10^{3}} \\\Rightarrow;I&=&0.87\cdot10^{-3}A \end{array}$
$\begin{array}{rcl}U_{S}&=&\dfrac{R_{2}}{R_{1}+R_{2}}U_{e}\\&=&\dfrac{4.7}{2.2+4.7}\times6.0\\ \Rightarrow\;U_{S}&=&4.1V \end{array}$
2.1 Représentation du schéma du circuit réalisé.
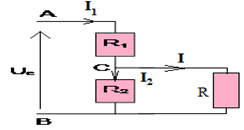
2.2. Détermination de la résistance équivalente $R_{e}$ à l'association des conducteurs ohmique de résistances $R_{2}$ et $R$
$\begin{array}{lll} R_{e}&=&\dfrac{R_{2}R}{R_{2}+R}\\&=& \dfrac{4.7\times 1.0}{4.7+1.0}\\ \Rightarrow\;R_{e}&=&0.82k\Omega \end{array}$
2.4 Déduction des intensités des courants dans les conducteurs de résistances $R_{1}$, $R_{2}$ et $R$
$\begin{array}{rcl} I_{1}&=&\dfrac{U_{e}}{R_{e}}\\&=& \dfrac{6.0}{3.02\cdot10^{3}}\\ \Rightarrow\;I_{1}&=&2\cdot10^{-3}A \end{array}$
$\begin{array}{rcl} U_{CB}&=&U_{AB}-U_{CA}\\ \Rightarrow\;R_{2}I_{2}&=&U_{e}-R_{1}I_{1}\\ \Rightarrow\;I_{2}&=& \dfrac{U_{e}-R_{1}I_{1}}{R_{2}}\\&=& \dfrac{6.0-2.2\cdot10^{3}\times2\cdot10^{-3}}{4.7\cdot10^{3}}\\ \Rightarrow\;I_{2}&=&0.34\cdot10^{-3}A \end{array}$
$\begin{array}{rcl} I&=&\dfrac{U_{e}-R_{1}I_{1}}{R}\\&=& \dfrac{6.0-2.2\cdot10^{3}\times2\cdot10^{-3}}{1\cdot10^{3}}\\ \Rightarrow\;I&=&1.6\cdot10^{-3}A \end{array}$
2.5 Montrons que la tension de sortie est alors $U_{S}^{\prime}$ différente de $U_{S}$
$\begin{array}{rcl} U_{S}&=&R_{2}I_{2}\\&=&4.7\cdot10^{3}\times0.34\cdot10^{-3}\\ \Rightarrow\;U_{S}&=&1.6V \end{array}$
$\begin{array}{rcl} U_{S}^{\prime}&=&R_{e}I\\&=&0.82\cdot10^{3}\times1.6\cdot10^{-3}\\ \Rightarrow\;U_{S}^{\prime}&=&1.3V\\ \Rightarrow\;U_{S}\neq U_{S}^{\prime} \end{array}$
Exercice 9
1.1 Le circuit est en série
2.2 Représentons le branchement des voltmètres (Voir figure)
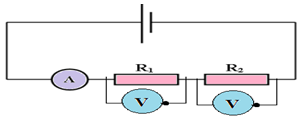
1.3 Rappel de la loi d'Ohm relative à un résistor.
$U=RI$
1.4 Calcul des tensions $U_{1}$ et $U_{2}$
$\begin{array}{rcl} U_{1}&=&R_{1}I\\&=&10\times0.2\\ \Rightarrow\;U_{1}&=&2V \end{array}$
$\begin{array}{rcl} U_{2}&=&R_{2}I\\&=&20\times0.2\\ \Rightarrow\;U_{2}&=&4V \end{array}$
1.4 Déduction de la tension aux bornes du générateur.
La loi d'additivité des tensions s'écrit :
$\begin{array}{rcl} U_{G}&=&U_{1}+U_{2}\\&=&2+4\\ \Rightarrow\;U_{G}&=&6V \end{array}$
1.6 Calcul de la résistance équivalente à cette association de $R_{1}$ et $R_{2}$
$\begin{array}{rcl} R_{\text{éq}}&=&R_{1}+R_{2}\\&=&10+20\\ \Rightarrow\;R_{\text{éq}}&=&30\Omega \end{array}$
2. On considère que la tension aux bornes du générateur reste constante.
On réalise avec les mêmes dipôles le deuxième circuit suivant :
2.1 Les résistors dans ce deuxième circuit sont associés en dérivation
Déduction de $R'_{\text{eq}}$ équivalente la résistance équivalente à cette association de $R_{1}$ et $R_{2}$
$\begin{array}{rcl} R'_{\text{eq}}&=&\dfrac{R_{1}R_{2}}{R_{1}+R_{2}}\\&=&\dfrac{10\times 20}{10+20}\\ \Rightarrow\;R'_{\text{eq}}&=&6.7\Omega \end{array}$
2.2 Il faut utiliser un voltmètre pour mesurer la tension $U'_{1}$ aux bornes de $R_{1}$ et $U_{2}^{\prime}$ aux bornes de $R_{2}$
Précisions la valeur de chacune de ces deux tensions
$U_{1}=U_{2}=6.0V$
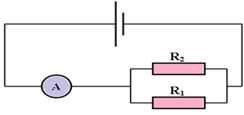
2.3 Calcul de l'intensité du courant $I_{1}$ traversant $R_{1}$
$\begin{array}{rcl} I_{1}&=&\dfrac{U_{1}}{R_{1}}\\&=& \dfrac{6.0}{10}\\ \Rightarrow\;I_{1}&=&0.60A \end{array}$
2.4 Calcul de l'intensité du courant $I_{2}$ traversant $R_{2}$
$\begin{array}{rcl} I_{2}&=&\dfrac{U_{2}}{U_{2}}\\&=& \dfrac{6.0}{20}\\ \Rightarrow\;I_{2}&=&0.30A \end{array}$
e. Déduisons l'intensité $I^{\prime}$ du courant mesurée par l'ampèremètre en précisant la loi utilisée.
On applique la loi des nœuds.
$\begin{array}{rcl} I'&=&I_{1}+I_{2}\\&=&0.60+0.30\\ \Rightarrow\;I'&=&0.90A \end{array}$
f. Calcul du rapport $\left(U_{\text{générateur}}/I'\right)$ et comparons le avec la résistance $R'_{\text{eq}}$ équivalent
$\begin{array}{rcl} U_{\text{Générateur}}/I'&=&\dfrac{6}{0.90}\\&=&6.7\Omega\\ \Rightarrow\;U_{\text{Générateur}}/I'&=&R'_{\text{eq}} \end{array}$
3. Comparons les intensités du courant $I$ et $I^{\prime}$
L'intensité $I^{\prime}$ délivrée par le générateur dans un montage série est supérieure à celle $I$ d'un montage en dérivation.
Exercice 10
1. Recopions le schéma avec le sens conventionnel du courant électrique
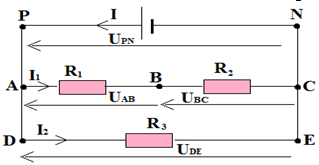
2. Calcul du nombre d'électrons traversant une section de la branche $PN$ pendant une seconde.
$\begin{array}{rcl} Q&=&ne\\&=&It\\ \Rightarrow\;n&=&\dfrac{It}{e}\\&=&\dfrac{69.5\cdot10^{-3}\times 1}{1.6\cdot10^{-19}}\\ \Rightarrow\;n&=&43\cdot10^{16}\text{élections} \end{array}$
3. Représentation des tensions positives aux bornes de chacun des dipôles (Voir figure)
Le courant électrique circule d'un état électrique élevé vers un état électrique moins élevé
4. Détermination des intensités $I_{1}$ et $I_{2}$
$\begin{array}{rcl} I_{2}&=&\dfrac{U_{DE}}{R_{3}}\\&=&\dfrac{U_{PN}}{R_{3}}\\&=& \dfrac{6.20}{220}\\ \Rightarrow\;I_{2}&=&28.2mA \end{array}$
$\begin{array}{rcl} I&=&I-I_{2}\\&=&69.5-28.21_{1}\\&=&41.3mA \end{array}$
5. Détermination des résistance $R_{1}$ et $R_{2}$ des conducteurs ohmiques de la branche $ABC$
$\begin{array}{rcl} R_{1}&=&\dfrac{U_{AB}}{I_{1}}\\&=& \dfrac{4.13V}{41.2\cdot 10^{-3}}\\ \Rightarrow\;R_{1}&=&100\Omega \end{array}$
$\begin{array}{rcl} R_{2}&=&\dfrac{U_{BC}}{I_{1}}\\&=&\dfrac{U_{PN}-U_{AB}}{I_{1}}\\&=&\dfrac{6.20-4.13}{41.2\cdot10^{-3}}\\ \Rightarrow\;R_{2}&=&50.2\Omega \end{array}$
Exercice 11
1. Rappel la définition de la caractéristique d'un dipôle.
La caractéristique d'un dipôle est le graphique sur lequel on représente les variations de la tension aux bornes d'un dipôle en fonction de l'intensité du courant ou inversement.
Les appareils de mesure nécessaires à sa détermination sont ; un voltmètre et ampèremètre
2. Représentation du schéma du montage électrique correspondant
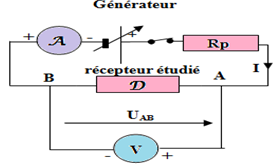
3. Tracé de la représentation graphique $U=f(I)$
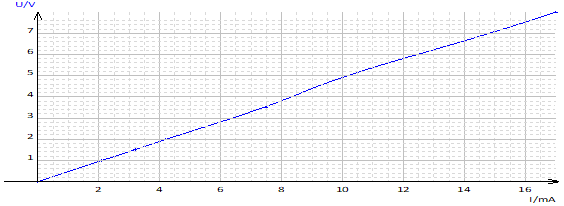
4. La courbe est une droite linéaire Qu'en déduit-on sur la nature du dipôle $D$ est un résistor ou un conducteur ohmique dont sa caractéristique est de la forme $U=aL$
5. Détermination de la valeur de la grandeur caractérisant le dipôle $D$
$\begin{array}{rcl} a&=&\dfrac{\Delta U}{\Delta I}\\&=&R\\\Rightarrow\;R&=&\dfrac{5-0}{10^{-3}-0}\\ \Rightarrow\;R&=&5\cdot10^{3}\Omega \end{array}$
Exercice 12
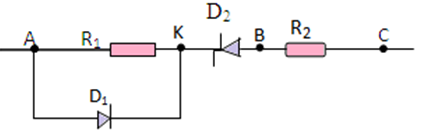
1. Le rôle de $D_{1}$ est de protéger le résistor de résistance $R_{1}$
Calcul de la résistance $R_{2}$ minimale pour que la diode $D_{2}$ soit protégée.
$\begin{array}{rcl} U_{BC}&=&U_{AC}-U_{RZ}\\ \Rightarrow\;R_{2}I_{RZ}&=&U_{AC}-U_{RZ}\\ \Rightarrow\;R_{2}&=&\dfrac{U_{AC}-U_{RZ}}{I_{RZ}}\\&=& \dfrac{12-8}{60\cdot10^{-3}}\\ \Rightarrow\;R_{2}&=&66.7\Omega \end{array}$
La diode $D_{1}$ est alors protégée
2. Calcul de la résistance $R_{1}$ pour que la diode $D_{2}$ soit protégée
$\begin{array}{rcl} U_{R_{1}}&=&U_{RM}\\&=&R_{1}I_{FM}\\ \Rightarrow\;R_{1}&=&\dfrac{U_{RM}}{I_{FM}}\\&=& \dfrac{100}{100\cdot10^{-3}}\\ \Rightarrow\;R_{1}&=&10^{3}\Omega \end{array}$
Exercice 14
1.Tracé la caractéristique de la VDR
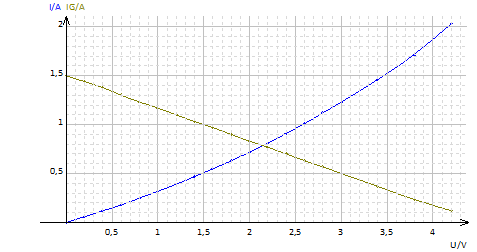
2. Relation qui existe entre l'intensité et la tension pour ce générateur
$\begin{array}{rcl} U_{G}&=&E-rI\\ \Rightarrow\;rI&=&-U_{G}+E\\ \Rightarrow\;I&=&-\dfrac{U_{G}}{r}+\dfrac{E}{r} \end{array}$
Tracé de la caractéristique de ce générateur (Voir graphe ci-dessous)
3. Détermination graphique de la valeur de l'intensité circulant dans le circuit et celles des tensions aux bornes de chacun des deux composants.
$U=U_{G}=2.15V$ ;
$I=I_{G}=0.75A$
4. Détermination de la relation entre l'intensité et la tension pour les deux branches générateur – conducteur $R$
$\begin{array}{rcl} U_{R}&=&U_{G}\\ \Rightarrow\;RI&=&E-rI\\ \Rightarrow\;(R+r)I&=&E\\ \Rightarrow\;I&=&\dfrac{E}{R+r} \end{array}$
$\begin{array}{rcl} I_{R}&=&\dfrac{E}{R+r}\quad\text{or}\quad U_{R}=RI_{R}\\&=&R\dfrac{E}{R+r}\\&=&0.87\times\dfrac{4.5}{0.87+3}\\ \Rightarrow\;U_{R}&=&U_{VDR}\\&=&U_{G}\\&=&1.01V \end{array}$
$\begin{array}{rcl} I_{R}&=&\dfrac{E}{R+r}\\&=&\dfrac{4.5}{0.87+3}\\ \Rightarrow\;I_{R}&=&1.16A \end{array}$
$\begin{array}{rcl} U_{G}&=&E-rI_{G}\\ \Rightarrow\;I&=&\dfrac{E-U_{G}}{r}\\&=& \dfrac{4.5-1.01}{3}\\ \Rightarrow\;I_{G}&=&1.16A \end{array}$
$\begin{array}{rcl} I_{VDR}&=&I_{G}-I_{G}\\&=&1.16-1.16\\ \Rightarrow\;I_{VDR}&=&0A \end{array}$
Exercice 15
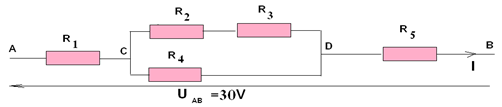
1. Détermination de la résistance équivalente du dipôle $CD$
$\begin{array}{rcl} R_{CD}&=&\dfrac{\left(R_{2}+R_{3}\right)R_{4}}{R_{2}+R_{3}+R_{4}}\\&=& \dfrac{(50+50)\times 50}{50+50+50}\\ \Rightarrow\;R_{CD}&=&33.3\Omega \end{array}$
2. Déduisons la résistance totale du dipôle $AB$
$\begin{array}{rcl} R_{AB}&=&R_{1}+R_{CD}+R_{5}\\&=&25+33.3+25\\ \Rightarrow\;R_{AB}&=&83.3\Omega \end{array}$
3. Détermination de l'intensité du courant $I$
$\begin{array}{rcl} I&=&\dfrac{U_{AB}}{R_{AB}}\\&=& \dfrac{30}{83.3}\\ \Rightarrow\;I&=&0.36A \end{array}$
4. Déduction des intensités $I_{2}$ et $I_{3}$ passant respectivement par $R_{4}$ et $\left(R_{2}+R_{3}\right)$
$\begin{array}{rcl} U_{CD}&=&U_{AB}-\left(R_{1}+R_{2}\right)I\\&=&30-(25+25)\times0.36\\ \Rightarrow\;U_{CD}&=&12V \end{array}$
$\begin{array}{rcl} I_{2}&=&\dfrac{U_{CD}}{R_{4}}\\&=& \dfrac{12}{50}\\ \Rightarrow\;I_{2}&=&0.24\Omega \end{array}$
$\begin{array}{rcl}I_{2}&=&\dfrac{U_{CD}}{R_{2}+R_{3}}\\&=& \dfrac{12}{50+50}\\ \Rightarrow\;I_{2}&=&0.12A \end{array}$
Exercice 16
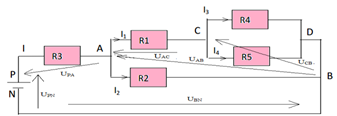
1. Représentons $U_{AB}$, $U_{PN}$, $U_{PA}$, $U_{CA}$, $U_{BN}$ et $U_{CB}$
2. $U_{BN}=0V$
3. Représentons le sens des courants (voir figure)
4. Calcul de $U_{PA}$
$\begin{array}{rcl} U_{PA}&=&U_{BA}+U_{PN}\\&=&-U_{AB}+U_{PN}\\&=&-8+12\\ \Rightarrow\;U_{PA}&=&4V \end{array}$
5. Calcul de $I$
$\begin{array}{rcl} U_{PA}&=&R_{3}I\\ \Rightarrow\;I&=&\dfrac{U_{PA}}{R_{3}}\\&=&\dfrac{4}{200}\\ \Rightarrow\;I&=&2\cdot10^{-2}A\\ \Rightarrow\;I&=&20mA \end{array}$
6. Calcul de $I_{2}$
$\begin{array}{rcl} I&=&I_{1}+I_{2}\\ \Rightarrow\;I_{2}&=&I-I_{1}\\&=&20-15\\ \Rightarrow\;I_{2}&=&5mA \end{array}$
7. Calcul de $R_{2}$
$\begin{array}{rcl} U_{AB}&=&R_{2}I_{2}\\ \Rightarrow\;R_{2}&=&\dfrac{U_{AB}}{I_{2}}\\&=&\dfrac{8}{5\cdot10^{-3}}\\ \Rightarrow\;I&=&1.6\cdot10^{3}A \end{array}$
8. Calcul de $R_{1}$
$\begin{array}{rcl} R_{1}&=&\dfrac{U_{AB}}{I_{1}}\\&=&\dfrac{6}{15\cdot10^{-3}}\\ \Rightarrow\;R_{1}&=&400\Omega \end{array}$
9. Calcul de $U_{CB}$
$\begin{array}{rcl} U_{CB}&=&U_{AB}-U_{AC}\\&=&8-6\\ \Rightarrow\;U_{CB}&=&2V \end{array}$
10. Calcul de $I_{3}$
$\begin{array}{rcl} I_{3}&=&\dfrac{U_{CB}}{R_{4}}\\&=&\dfrac{2}{200}\\ \Rightarrow\;I_{3}&=&10mA \end{array}$
11. Calcul de $I_{4}$
$\begin{array}{lll} I_{4}&=&I_{1}-I_{1}\\&=&15-10\\ \Rightarrow\;I_{4}&=&5mA \end{array}$
12. Calcul de $R_{5}$
$\begin{array}{rcl} U_{CB}&=&U_{AB}-U_{AC}\\&=&R_{5}I_{4}\\ \Rightarrow\;R_{5}&=&\dfrac{U_{AB}-U_{AC}}{I_{4}}\\&=&\dfrac{8-6}{5\cdot10^{-3}}\\ \Rightarrow\;R_{5}&=&400\Omega \end{array}$
13. Calcul de $R_{\text{éq}}$ la résistance équivalente
$\begin{array}{rcl} R_{CD}&=&\dfrac{R_{4}R_{3}}{R_{3}+R_{4}}\\&=&\dfrac{200\times 200}{200+200}\\ \Rightarrow\;R_{CD}&=&100\Omega \end{array}$
$\begin{array}{rcl} R_{AD}&=&R_{1}+R_{CD}\\&=&400+100\\ \Rightarrow\;R_{AD}&=&500\Omega \end{array}$
$\begin{array}{rcl} R_{AD}^{\prime}&=&\dfrac{R_{2}R_{AD}}{R_{2}+R_{AD}}\\&=&\dfrac{1600\times 500}{1600+500}\\ \Rightarrow\;R'_{AD}&=&381\Omega \end{array}$
$\begin{array}{rcl} R_{\text{équi}}&=&R_{3}+R^{\prime}_{AD}\\&=&200+381\\\Rightarrow\;R_{\text{équi}}&=&581\Omega \end{array}$
Exercice 17
$\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|} \hline U(V)&0&2.0&5.0&5.2&5.5&5.6&5.7&5.8&5.82&5.86&5.90\\ \hline I(mA)&0&0&1.0&2.0&5.0&10&20&30&60&100&150\\ \hline \end{array}$
1. Tracé de la caractéristique courant-tension de cette diode
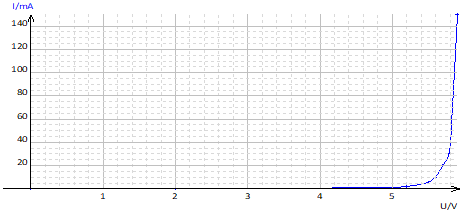
2. La valeur de $R$ pour que la tension aux bornes de la diode
$\begin{array}{lll} R&=&\dfrac{U}{I}\\&=& \dfrac{5.6}{10^{-3}}\\ \Rightarrow\;R&=&5.6\cdot10^{3}\Omega \end{array}$

Ajouter un commentaire