Solution des exercices : Effet Photoélectrique - Ts

 

a) Calcul du travail d'extraction $W_{O}$

 

$\begin{array}{lll} W_{0}&=&E-E_{C}\\\\&=&\dfrac{h_{C}}{\lambda}-E_{C}\\\\&=&\dfrac{6.62\cdot 10^{-34}\times 3.00\cdot 10^{8}}{0.150\cdot 10^{-6}\times 1.6\cdot 10^{-19}}-4.8\\\\\Rightarrow\,W_{0}&=&3.5eV \end{array}$

 

b) Nature du métal 

 

$\begin{array}{lll} \lambda_{0}&=&\dfrac{h_{C}}{W_{0}}\\\\&=&\dfrac{6.62\cdot 10^{-34}\times 3.00\cdot 10^{8}}{3.5\times 1.6\cdot 10^{-19}}\\\\\Rightarrow\lambda_{0}&=&3.5\cdot 10^{-7}\\\\&=&0.35\mu m \end{array}$

 

La longueur d'onde seuil correspond à celle du zinc ; le métal est le zinc

 

c) Tension nécessaire pour arrêter cette émission

 

$\begin{array}{lll} e\left|U\right|&=&E_{C}\\\\\Rightarrow\,e\left|U\right|&=&4.8eV\\\\\Rightarrow\left|U\right|&=&4.8V\\\\\Rightarrow\,U&=&-4.8V \end{array}$

 

d) Pour augmenter la vitesse maximale d'émission, il faut changer la longueur d'onde de la lumière en la diminuant. 

1) Description d'une cellule photoélectrique dite cellule photoémissive à vide.

 

 

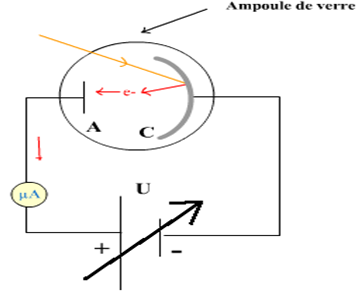
a) Énergie d'extraction $W_{O}$ d'un électron 

 

$\begin{array}{lll} W_{0}&=&\dfrac{h_{C}}{\lambda_{0}}\\\\&=&\dfrac{6.62\cdot 10^{-34}\times 3\cdot 10^{8}}{0.66\cdot 10^{-6}}\\\\\Rightarrow\,W_{0}&=&3.0\cdot 10^{-19}J \end{array}$ 

 

b) Détermination de l'énergie cinétique maximale $E_{C}$ d'un électron émis au niveau de la cathode. 

 

$\begin{array}{lll} E_{C}&=&\dfrac{h_{C}}{\lambda}-W_{0}\\\\&=&\dfrac{6.62\cdot 10^{-34}\times 3\cdot 10^{8}}{0.44\cdot 10^{-6}}-3.0\cdot 10^{-19}\\\\\Rightarrow\,E_{C}&=&4.5\cdot 10^{-19}J\\\\E_{C}&=&\dfrac{4.5\cdot 10^{-19}}{1.6\cdot 10^{-19}}\\\\\Rightarrow\,E_{C}&=&2.0eV \end{array}$

1) Expression de l'énergie cinétique de l'électron en fonction de la fréquence $\lambda$ et du travail d'extraction $W_{O}$

 

$E_{C}=\dfrac{h_{C}}{\lambda}-W_{0}$

 

2) Schéma du montage utilisé.

 

 

Expression de la tension d'arrêt en fonction de $\lambda$ et $W_{0}$

 

\begin{eqnarray} eU &=&hv-W_{0}\nonumber\\\\\Rightarrow\,U&=&\dfrac{h}{e}v-\dfrac{W_{0}}{e} \end{eqnarray}

 

3) Calcul des fréquences $\lambda$ des radiations utilisées  

 

\begin{eqnarray} v&=&\dfrac{c}{\lambda}\nonumber\\\\&=&\dfrac{3.0\cdot 10^{8}}{0.60\cdot 10^{-6}}\nonumber\\\\\Rightarrow\,v&=&5\cdot 10^{14}Hz\ ; \end{eqnarray}

 

$v=6\cdot 10^{14}Hz$ ;

 

$v=7.5\cdot 10^{14}Hz$ ;

 

$v=10\cdot 10^{14}Hz$ 

   

4) Tracer la courbe représentant la fonction $U=f(υ)$ 

$$\begin{array}{|l|c|c|c|c|} \hline U(V)&0.19&0.60&1.22&2.26\\ \hline v(Hz)&5\cdot 10^{14}&6\cdot 10^{14}&7.5\cdot 10^{14}&10\cdot 10^{14}\\ \hline \end{array}$$

 

 

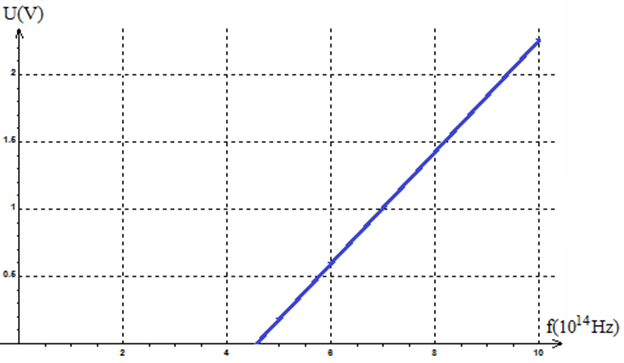
Fréquence $υ_{0}$ du seuil photoélectrique du césium.

 

$v_{0}=5\cdot 10^{14}Hz$

 

Longueur d'onde $\lambda_{0}$ du seuil photoélectrique.

 

\begin{eqnarray} \lambda_{0}&=&\dfrac{c}{v_{0}}\nonumber\\\\&=&\dfrac{3\cdot 10^{8}}{5\cdot 10^{14}}\nonumber\\\\\Rightarrow\lambda_{0}&=&0.6\cdot 10^{-6}m \end{eqnarray}

1) Expression de l'énergie d'un photon de fréquence $\lambda$

 

$E=\dfrac{h_{C}}{\lambda}$ 

  

Expression de l'énergie maximale des électrons émis par la cathode en fonction de $U_{0}$

 

$E_{\text{max}}=eU_{0}$

 

$\begin{array}{lll} E&=&E_{\text{max}}+W_{0}\\\\\Rightarrow\,hv&=&eU_{0}+W_{0}\\\\\Rightarrow\,U_{0}&=&\dfrac{h}{e}v-\dfrac{W_{0}}{e} \end{array}$ 

 

2) Représentation graphique des variations de $U_{0}$ en fonction de $v$

 

 

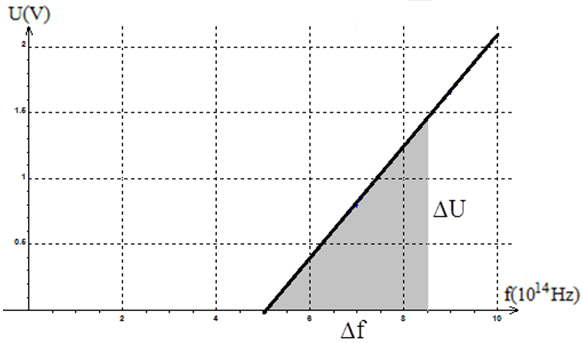
En déduire le seuil de fréquence $v_{0}$ de la cellule, la constante de Planck $h$ et $W_{0}$ (exprimé en électron-volt)

 

$v_{0}=5\cdot 10^{14}Hz$

 

$U_{0}=\dfrac{h}{e}v-\dfrac{W_{0}}{e}$ C'est une droite de coefficient directeur $\dfrac{h}{e}.$

 

$\begin{array}{lll} \dfrac{h}{e}&=&\dfrac{\Delta U_{0}}{\Delta f}\\\\\Rightarrow\,h&=&e\times\dfrac{\Delta U_{0}}{\Delta f}\\\\&=&1.6\cdot 10^{-19}\times\dfrac{1.52-0}{8.5\cdot 10^{14}-5\cdot 10^{14}}\\\\\Rightarrow\,h&=&6.95\cdot 10^{-34}J\cdot s \end{array}$

1) Détermination graphique l'équation de la courbe représentant $\left|U_{0}\right|=f\left(\dfrac{1}{\lambda}\right)$

 

 

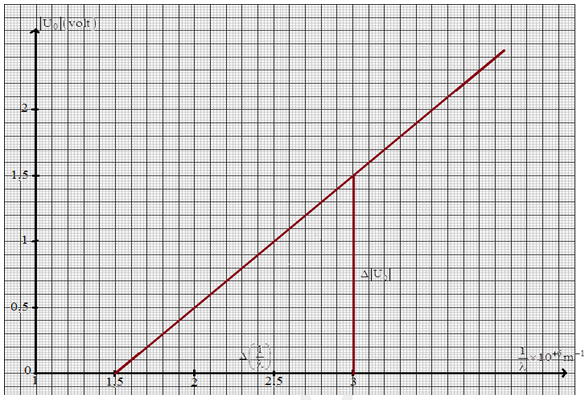
C'est une de la forme : $\left|U_{0}\right|=a\dfrac{1}{\lambda}+b$

 

$\begin{array}{lll} a&=&\dfrac{\Delta\left|U_{0}\right|}{\Delta\left(\dfrac{1}{\lambda}\right)}\\\\&=&\dfrac{1.5-0}{(3-1.5)\times 10^{6}}\\\\\Rightarrow\,a&=&10^{-6} \end{array}$                                                                                                                                                                                                                                                                                                                                  

 

$\begin{array}{lll} \left|U_{0}\right|&=&0\\\\\Rightarrow\,a\dfrac{1}{\lambda}+b&=&0\\\\\Rightarrow\,b&=&-a\dfrac{1}{\lambda}\\\\&=&-10^{-6}\times 1.5\cdot 10^{6}\\\\\Rightarrow\,b&=&-1.5V\\\\\Rightarrow\left|U_{0}\right|&=&10^{-6}\dfrac{1}{\lambda}-1.5 \end{array}$

 

2) a) Relation entre le potentiel d'arrêt $U_{0}$, le travail d'extraction $W_{0}$ d'un électron du métal de la cathode et l'énergie $W$ d'un photon incident.

 

$W=W_{0}+E_{C}=e\left|U_{0}\right|+W_{0}$

 

Expression de $\left|U_{0}\right|$ en fonction de $\dfrac{1}{\lambda}$ 

 

$\begin{array}{lll} W&=&e\left|U_{0}\right|+W_{0}\\\\\Rightarrow\dfrac{h_{C}}{\lambda}&=&e\left|U_{0}\right|+W_{0}\\\\\Rightarrow\left|U_{0}\right|&=&\dfrac{h_{C}}{e}\dfrac{1}{\lambda}-\dfrac{W_{0}}{e} \end{array}$

 

b) Détermination de la valeur approchée de la constante de Planck $h$

 

$\left|U_{0}\right|=10^{-6}\dfrac{1}{\lambda}-1.5\ ;$

 

$\begin{array}{lll} \left|U_{0}\right|&=&\dfrac{h_{C}}{e}\dfrac{1}{\lambda}-\dfrac{W_{0}}{e}\\\\\Rightarrow\dfrac{h_{C}}{e}&=&a\\\\\Rightarrow\,h&=&\dfrac{ae}{c}\\\\&=&\dfrac{10^{-6}\times 1.6\cdot 10^{-19}}{3\cdot 10^{8}}\\\\\Rightarrow\,h&=&5.4\cdot 10^{-34}J\cdot s\end{array}$ 

 

Calcul de $W_{0}$

 

$-\dfrac{W_{0}}{e}=-1.5\Rightarrow\,W_{0}=1.5eV$

 

3) a) Calcul de l'énergie $W$

 

$\begin{array}{lll} W&=&\dfrac{h_{C}}{\lambda}\\\\&=&\dfrac{6.62\cdot 10^{-34}\times 3\cdot 10^{8}}{0.588\cdot 10^{-6}}\\\\\Rightarrow\,W&=&3.4\cdot 10^{-19}J \end{array}$

 

d) Calcul de la vitesse maximale d'émission d'un électron par la cathode

 

$\begin{array}{lll} E_{C}&=&W-W_{0}\\\\\Rightarrow\dfrac{1}{2}mv^{2}\Rightarrow\,v&=&\sqrt{\dfrac{2}{m}\left(W-W_{0}\right)}\\\\&=&\sqrt{\dfrac{2}{9.1\cdot 10^{-31}}\left(3.4\cdot 10^{-19}-1.5\times 1.6\cdot 10^{-19}\right)}\\\\\Rightarrow\,v&=&4.7\cdot 10^{5}m\cdot s^{-1} \end{array}$

1) Valeur $\lambda_{0}$ de la longueur d'onde du seuil photoélectrique

 

$\begin{array}{lll} W_{0}&=&\dfrac{h_{C}}{\lambda_{0}}\\\\\Rightarrow\lambda_{0}&=&\dfrac{h\times c}{W_{0}}&=&\dfrac{6.62\cdot 10^{-34}\times 3\cdot 10^{8}}{2.5\times 1.6\cdot 10^{-19}}\\\\\Rightarrow\lambda_{0}&=&497nm \end{array}$

 

2) a) Les valeurs de $\lambda_{1}$ et $\lambda_{2}$

 

Les électrons sont extraits du métal que si les longueurs d'onde des photons incidents sont inférieures à la longueur d'onde seuil $\lambda\leq\lambda_{0}$

 

$\lambda_{1}=413.7nm$ ;

 

$\lambda_{2}=451.4nm$ ;

  

b) Montrons que l'expression du potentiel d'arrêt s'écrit $U_{0}=-\dfrac{E_{C}}{e}$

 

Le théorème de l'énergie cinétique appliqué l'électron s'écrit :

 

$\begin{array}{lll} \Delta E_{C}&=&\sum\,W_{\overrightarrow{F}}\\\\\Rightarrow\,E_{C}-0&=&-eU_{0}\\\\\Rightarrow\,U_{0}&=&-\dfrac{E_{C}}{e} \end{array}$

  

a) Calcul de la valeur du potentiel d'arrêt correspondant à chacune des deux radiations

 

$\begin{array}{lll} U_{01}&=&\dfrac{h_{C}}{e}\dfrac{1}{\lambda_{1}}-\dfrac{W_{0}}{e}\\\\&=&\dfrac{6.62\cdot 10^{-34}\times 3\cdot 10^{8}}{413.7\cdot 10^{-9}\times 1.6\cdot 10^{-19}}-2.5\\\\\Rightarrow\,U_{01}&=&0.50V \end{array}$

 

$\begin{array}{lll} U_{02}&=&\dfrac{h_{C}}{e}\dfrac{1}{\lambda_{2}}-\dfrac{W_{0}}{e}\\\\&=&\dfrac{6.62\cdot 10^{-34}\times 3\cdot 10^{8}}{451.4\cdot 10^{-9}\times 1.6\cdot 10^{-19}}-2.5\\\\\Rightarrow\,U_{02}&=&0.25V \end{array}$

 

3) Détermination de la valeur du potentiel d'arrêt correspondant à cette expérience

 

$U_{0}=U_{01}=0.50V.$ Car c'est la valeur la plus élevée.