Solution des exercices : Les alcanes - 1er s
Classe:
Première
Exercice 1
1. Nommons les alcanes suivants
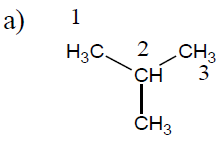
$2-$méthylpropane ou méthylpropane
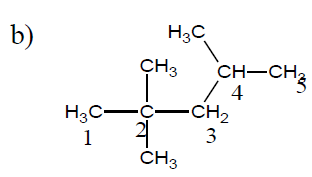
$2\;,\ 2\;,\ 4-$trimétylpentane
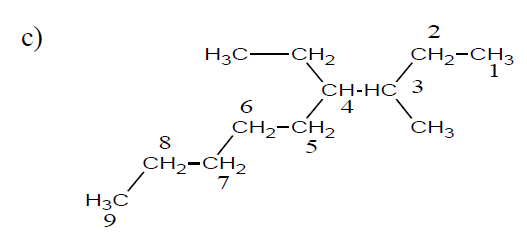
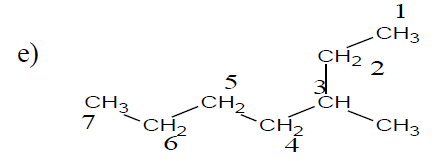
$4-$éthyl$-3-$méthylnonane
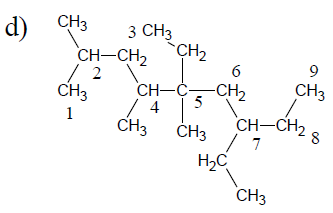
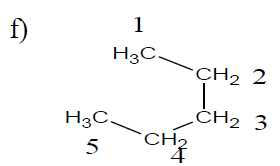
$5\;,\ 7-$diéthyl$-2\;,\ 4\;,\ 5-$triméthylnonane
$3-$méthylhéptane
Pentane
$4$éthyl$-3-$méthylhexane
$6-$éthyl$-2\;,\ 3-$diméthyldécane
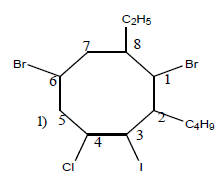
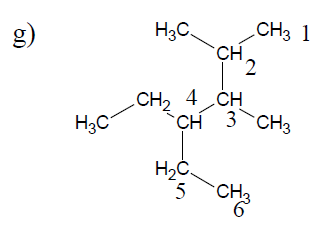
$1\;,\ 6-$dibromo$-2-$butyl$-4-$chloro$-8-$éthyl$-3-$iodocyclooctane
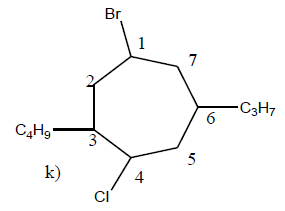
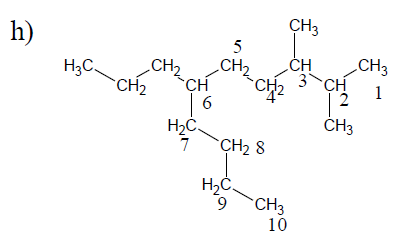
$1-$bromo$-3-$butyl$-4-$chioro$-6-$propyjhéptane
2. Écriture des formules semi développées des hydrocarbures suivants :
2.1. $\ 3-$éthyl$-2-$methylhexane :
$CH_{3}-CH_{2}-CH_{2}-CH\left(C_{2}H_{5}\right)-CH\left(CH_{3}\right)-CH_{3}$
2.2. $\ 2\;,\ 3-$dimethylpentane
$CH_{3}-CH_{2}-CH\left(CH_{3}\right)-CH\left(CH_{3}\right)-CH_{3}$
2.3. $\ 4-$éthyl$-2\;,\ 5-$méthylheptane
$CH_{3}-CH\left(CH_{3}\right)-CH\left(C_{2}H_{5}\right)-CH_{2}-CH\left(CH_{3}\right)-CH_{3}$
2.4. $\ 3\;,\ 4-$diéthylhexane
$CH_{3}-CH_{2}-CH\left(C_{2}H_{5}\right)-CH\left(C_{2}H_{5}\right)-CH_{2}-CH_{3}$
2.5. $\ 3-$éthyl$-2\;,\ 3-$diméthylhexane
2.6. $\ 2\;,\ 2-$diméthyl$-5\;,\ 6-$dipropylnonane
2.7. $\ 4-$éthyl$-3-$méthyl$-5-$propyloctane
2.8. $\ 2\;,\ 2\;,\ 3\;,\ 3-$tétraméthylpentane
3. Les formules semi-développées qui correspondent aux noms suivants.
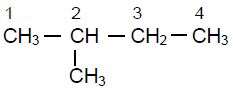
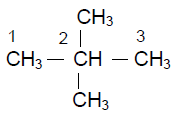
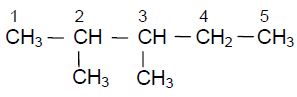
a) $4-$propyldécane
$CH_{3}-CH_{2}-CH_{2}-CH\left(C_{3}H_{7}\right)-\left(CH_{2}\right)_{5}-CH_{3}$
b) $3-$éthyl $4-$méthylnonane
$CH_{3}-CH_{2}-CH\left(C_{2}H_{5}\right)-CH\left(CH_{3}\right)-\left(CH_{2}\right)_{4}-CH_{3}$
c) $2\;,\ 2-$diméthylbutane
$CH_{3}-CH\left(CH_{3}\right)_{2}CH_{2}-CH_{3}$
d) $4-$éthylnonane
$CH_{3}-CH_{2}-CH_{2}-CH\left(C_{2}H_{5}\right)-\left(CH_{2}\right)_{4}-CH_{3}$
e) $4\;,\ 4\;,\ 6\;,\ 6-$tétraméthyloctane
$CH_{3}-CH_{2}-CH_{2}-CH\left(CH_{3}\right)_{2}-CH_{2}-CH_{2}-CH\left(CH_{3}\right)_{2}-CH_{3}$
Le nom est incorrect ; le nom correct est $2\;,\ 2\;,\ 5\;,\ 5-$tétraméthyloctane
f) $1\;,\ 3-$diéthylpropane
$CH_{3}\left(C_{2}H_{5}\right)_{2}-CH_{2}-CH_{3}\left(C_{2}H_{5}\right)_{2}$
Le nom est incorrect ; le nom correct est $4-$éthyl$-5-$méthyl octane
h) $4-$méthyl$-1\;,\ 3-$diéthylpentane
$CH_{3}-CH\left(CH_{3}\right)-CH\left(C_{2}H_{5}\right)-CH_{2}-CH_{2}\left(C_{2}H_{5}\right)$
Le nom est incorrect ; le nom correct est le $2-$méthyl$-3-$méthylheptane
i) $2-$éthyl$-3-$méthyl$-4-$propylnonane
$CH_{3}-CH\left(C_{2}H_{5}\right)-CH\left(CH_{3}\right)-CH\left(C_{3}H_{7}\right)-\left(CH_{2}\right)_{4}-CH_{3}$
j) $2\;,\ 3\;,\ 4-$triméthylpentane
$CH_{3}-CH\left(CH_{3}\right)-CH\left(CH_{3}\right)-CH\left(CH_{3}\right)-CH_{3}$
k) $2-$méthylbutane
$CH_{3}-CH\left(CH_{3}\right)-CH_{2}-CH_{3}$
l) $3\;,\ 5-$diméthylnonane
$CH_{3}-CH_{2}-CH\left(CH_{3}\right)-CH_{2}-CH\left(CH_{3}\right)-\left(CH_{2}\right)_{3}-CH_{3}$
Exercice 2
1.1. Des isomères sont des corps de même formule brute mais dont les formules développées sont différentes.
Les molécules ont donc des structures différentes et des propriétés différentes, parfois même très différentes.
1.2. Les isomères du pentane sont :
$CH_{3}-CH_{2}-CH_{2}-CH_{2}-CH_{3}$
Pentane
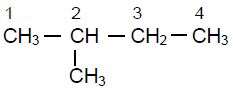
$2-$méthylbutane
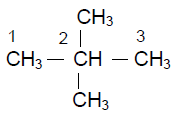
$2\;,\ 2-$diméthylpropane ou diméthylpropane
2. La molécule proposée :
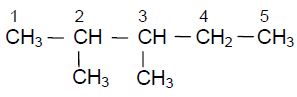
est du $2\;,\ 3-$diméthylpentane.
3.
3.1. La formule générale d'un alcane à chaîne ouverte et à $n$ atomes de carbone est : $C_{n}H_{2n+2}.$
3.2. La masse molaire $M$ de l'alcane peut s'exprimer en fonction de $n$ :
$M=n\cdot M_{C}+(2n+2)\cdot M_{H}.$
$M=n\times 12+(2n+2)\times 1$
$\boxed{M=14n+2}$
3.3. Pour l'alcane considéré la masse molaire est $114\,g\cdot mol^{-1}.$
On peut donc écrire :
$14n+2=114$
$\Rightarrow 14n=112$
d'où $n=8$
La formule brute de l'alcane est $C_{8}H_{18}.$
3.4. L'alcane de formule $C_{8}H_{18}$ est l'octane
Exercice 3
1. Rappel de la définition d'un hydrocarbure aliphatique.
Un hydrocarbure aliphatique est un composé organique constitué d'atomes de carbone et d'hydrogène à chaine ouverte.
2. Équation de la réaction.
$C_{x}H_{y}+\left(x+\dfrac{y}{4}\right)O_{2}\rightarrow x CO_{2}+\dfrac{y}{2}H_{2}O$
3. a) Calcul du nombre de moles de $(A)$ présent dans l'échantillon
$n_{A}=\dfrac{m_{A}}{M_{A}}=\dfrac{0.72}{72}\Rightarrow n_{A}=0.01\,mol$
b) Montrons que $(A)$ a pour formule brute $C_{5}H_{12}.$
Déterminons le nombre de dioxyde de carbone et de l'eau
$n_{CO_{2}}=\dfrac{V_{CO_{2}}}{V_{M}}=\dfrac{1.2}{24}\Rightarrow n_{CO_{2}}=0.05\,\text{mol}$
$n_{H_{2}O}=\dfrac{m_{H_{2}O}}{M_{H_{2}O}}=\dfrac{1.08}{18}\Rightarrow n_{A}=0.06\,\text{mol}$
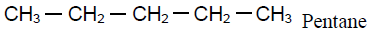
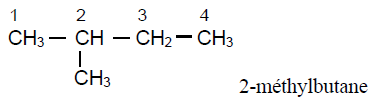
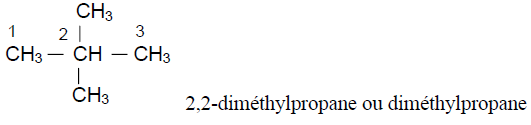
D'après le bilan molaire :
$\begin{array}{rcl} n_{A}=\dfrac{n_{CO_{2}}}{x}=\dfrac{n_{H_{2}O}}{\dfrac{y}{2}}&\Rightarrow & \left\lbrace\begin{array}{lcl}\dfrac{n_{H_{2}O}}{\dfrac{y}{2}} &=&n_{A}\\\\\dfrac{n_{CO_{2}}}{x} &=&n_{A} \end{array}\right.\\\\&\Rightarrow &\left\lbrace\begin{array}{lcl}\dfrac{2\times 0.06}{0.01} &=&y\\\\\dfrac{0.05}{0.01} &=&x \end{array}\right.\\\\&\Rightarrow &\left\lbrace\begin{array}{lcl}y &=&12\\\\\ x &=&5 \end{array}\right.\\\\ &\Rightarrow & C_{5}H_{12} \end{array}$
4. Formules semi - développées des isomères de $(A)$ et leur nom respectif.
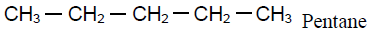
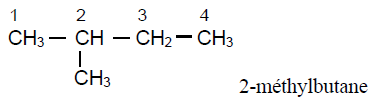
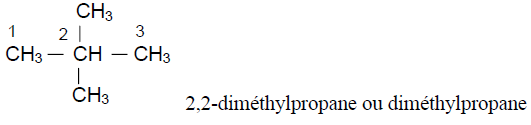
Exercice 4
1. Équation-bilan de la réaction de combustion en fonction de $x$ et $y.$
$C_{x}+H_{y}+\left(x+\dfrac{y}{4}\right)\;O_{2}\ \rightarrow\ xCO_{2}\ +\ \dfrac{y}{2}H_{2}O$
2. Le volume de dioxygène en excès
$V_{5}=V_{3}-V_{4}+65-40$
$\Rightarrow V_{5}=25\,cm^{3}$
Déduction du volume de dioxygène réagi.
$V_{6}=V_{2}-V_{5}+90-25$
$\Rightarrow V_{6}=65\,cm^{3}$
3. Montrons que la formule moléculaire brute de l'hydrocarbure $A$ est $C_{4}H_{10}.$
D'après le bilan volumique :
$\begin{array}{rcl} V_{1} = \dfrac{V_{2}}{x}=\dfrac{V_{6}}{x+\dfrac{y}{4}}&\Rightarrow&\left\lbrace \begin{array}{lcl} V_{1} &=& \dfrac{V_{2}}{x} \\ V_{1} &=&\dfrac{V_{6}}{x+\dfrac{y}{4}} \end{array}\right.\\\\&\Rightarrow&\left\lbrace \begin{array}{lcl} x&=&\dfrac{V_{2}}{V_{1}}\\ x+\dfrac{y}{4} &=&y\dfrac{V_{6}}{V_{1}} \end{array}\right.\\\\&\Rightarrow&\left\lbrace \begin{array}{lcl} x &=&\dfrac{40}{10}\\ x+\dfrac{y}{4} &=&\dfrac{65}{10} \end{array}\right.\\\\&\Rightarrow&\left\lbrace \begin{array}{lcl} x&=&\dfrac{40}{10}\\ y&=&\left(\dfrac{65}{10}-x\right)\end{array}\right.\\\\&\Rightarrow&\left\lbrace \begin{array}{lcl} y&=& 4\\x&=&10 \end{array}\right.\\\\&\Rightarrow&\boxed{C_{4}H_{10}}\end{array}$
4. Formule semi-développée exacte et nom de l'alcane $A$ sachant qu'il contient une chaine carbonée ramifiée.
$$CH_{3}-CH\left(CH_{3}\right)-CH_{3}$$
5.1 Rappel des conditions expérimentales : il faut la lumière comme catalyseur et utiliser une solution de sel
Équation-bilan de la réaction en utilisant les formules brutes.
$C_{4}H_{10}\ +\ Cl_{2}\ \rightarrow\ C_{4}H_{9}Cl\ +\ HCl$
5.2. Les formules et les noms des deux dérivés monochlorés qui se forment
$CH_{2}Cl-CH\left(CH_{3}\right)-CH_{3}$ : $1-$Chloro$-2-$méthylpropane
$CH_{3}-CCl\left(CH_{3}\right)-CH_{3}$ : $2-$Chloro$-2-$méthylpropane
Exercice 5
1. Écriture d'une première relation entre les volumes $V_{1}$ et $V_{2}.$
$V_{1}+V_{2}=10L$
2. Équations-bilans des réactions de combustions du méthane et du propane avec le dioxygène.
$$CH_{4}\ +\ 2O_{2}\ \rightarrow\ CO_{2}\ +\ 2H_{2}O$$
$$C_{3}H_{8}\ +\ 5O_{2}\ \rightarrow\ 3CO_{2}\ +\ 4H_{2}O$$
3.1 Exprimons en fonction de $V_{1}$ et $V_{2}.$
les volumes de dioxygène consommés par la combustion complète des volumes $V_{1}$ et $V_{2}.$
D'après le bilan volumique :
$\left\lbrace\begin{array}{lcl}V_{1}&=&\dfrac{V_{01}}{2}\\\\ V_{2}&=&\dfrac{V_{02}}{5} \end{array}\right.\Rightarrow\left\lbrace\begin{array}{lcl}V_{01}&=&2V_{1}\\V_{02}&=&5V_{2} \end{array}\right.$
3.2 Déduction du volume $V_{0}$ de dioxygène nécessaire à la combustion complète du mélange en fonction de $V_{1}$ et $V_{2}.$
$V_{0}=V_{01}+V_{02}=2V_{1}+5V_{2}$
4. Déduction des valeurs de $V_{1}$ et $V_{2}.$
$\begin{array}{rcl}\left\lbrace\begin{array}{lcl} V_{1}+V_{2} &=& 10L\\ 2V_{1}+5V_{2} &=& 38L \end{array}\right.&\Rightarrow&\left\lbrace\begin{array}{lcl} 2\left(V_{1}+V_{2}\right) &=&10L\\ 2V_{1}+5V_{2} &=&38L\end{array}\right.\\\\&\Rightarrow&\left\lbrace\begin{array}{lcl} 2V_{1}+2V_{2} &=&20L\\ 2V_{1}+5V_{2} &=&38L\end{array}\right.\\\\&\Rightarrow&\left\lbrace\begin{array}{lcl} V_{1}&=&4L\\ V_{2}&=&6L \end{array}\right.\end{array}$
5. Détermination de la composition centésimale volumique du mélange étudié.
$\begin{array}{rcl} \% CH_{4} &=&\dfrac{V_{1}\times 100}{V_{1}+V_{2}}\\\\ &=& \dfrac{4\times 100}{4+6}\\\\\Rightarrow\% CH_{4} &=&40\ ; \end{array}$
$\begin{array}{rcl} \% C_{3}H_{8} &=&\dfrac{V_{2}\times 100}{V_{1}+V_{2}}\\\\ &=& \dfrac{6\times 100}{4+6}\\\\\Rightarrow\% C_{3}H_{8} &=&60 \end{array}$

Commentaires
Anonyme (non vérifié)
sam, 12/07/2024 - 18:50
Permalien
Merci mais je veux la
Anonyme (non vérifié)
sam, 12/07/2024 - 18:59
Permalien
Merci mais je veux avoir La
Anonyme (non vérifié)
sam, 12/21/2024 - 06:44
Permalien
Merci beaucoup
Kouraba (non vérifié)
mar, 01/07/2025 - 20:37
Permalien
Être meilleur
Anonyme
mar, 01/07/2025 - 20:39
Permalien
Apprendre
Pages
Ajouter un commentaire