solution des exercices : travail et puissant mécanique - 1er S

 

Exercice 8

 

a. Bilan des forces extérieurs s'appliquant au traîneau 

 

$\overrightarrow{T}$ : force des traction exercée par les chiens, 

 

$\overrightarrow{R}$ : réaction du plan inclinée, 

 

$\overrightarrow{f}$ : force de frottement 

 

et $\overrightarrow{P}$ : Poids du traîneau

 

Représentation des forces sur un schéma 

 

 

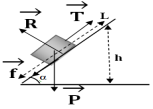
b. Résultante de ces forces

 

Le système évolue à vitesse constante, le principe de l'inertie s'écrit :

$$\overrightarrow{T}+\overrightarrow{P}+\overrightarrow{R}+\overrightarrow{f}=\overrightarrow{O}$$

 

La résultante de ces forces est donc nulle

 

c. Calcule du travail du poids $\overrightarrow{P}$ et du travail de la force de frottement $\overrightarrow{f}$

 

$\begin{array}{rcl} W\left(\overrightarrow{P}\right)&=&-mgh\\ &=&-mgL\sin\alpha&=&-110\times 500\times\dfrac{6.0}{100}&\rightarrow&\\ W\left(\overrightarrow{P}\right)&=&\\ -33.10^{3}J \end{array}$

 

$\begin{array}{rcl} W\left(\overrightarrow{f}\right)&=&-70\times 500\\ &\Rightarrow&W\left(\overrightarrow{f}\right)&=&-35\cdot 10^{3}J \end{array}$

 

d. Déduction du travail de la force de traction $\overrightarrow{T}$ exercée par les chiens sur le traîneau pour un déplacement de longueur $L$

 

$\begin{array}{rcl} \overrightarrow{T}+\overrightarrow{P}+\overrightarrow{\mathbb{R}}+\overrightarrow{f}&=&0\\ &\Rightarrow&\overrightarrow{T}\overrightarrow{L}+\overrightarrow{P}\overrightarrow{L}+\overrightarrow{R}\overrightarrow{L}+\overrightarrow{f}\overrightarrow{L}&=&\overrightarrow{O}\overrightarrow{L}\\ &\Rightarrow&W(T)+W\left(\overrightarrow{P}\right)+W\left(\overrightarrow{R}\right)+W\left(\overrightarrow{f}\right)&=&0

\end{array}$

 

Or

 

$\begin{array}{rcl} W\left(\overrightarrow{T}\right)&=&0\\ &\Rightarrow&W\left(\overrightarrow{T}\right)+W\left(\overrightarrow{P}\right)+W\left(\overrightarrow{f}\right)&=&\\ &\Rightarrow&W\left(\overrightarrow{T}\right)&=&-W\left(\overrightarrow{P}\right)-W\left(\overrightarrow{f}\right)&=&-\left(-33\cdot10^{3}\right)-\left(-35\cdot10^{3}\right)\\&\Rightarrow&W\left(\overrightarrow{T}\right)\\68\cdot10^{3}\,J \end{array}$

 

Puissance moyenne de cette force

 

$P_{m}\left(\overrightarrow{T}\right)=\overrightarrow{T}\overrightarrow{V}&=&TV\text{ or }T=\dfrac{W(T)}{L}\\ &\Rightarrow&P_{m}\left(\overrightarrow{T}\right)&=&\dfrac{W(T)}{L}V&=&\dfrac{68\cdot10^{3}}{500}\times 6.94\\&\Rightarrow&P_{m}\left(\overrightarrow{T}\right)&=&9.4\cdot10^{2}W$

 

Exercice 9

 

 

 

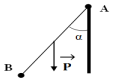
a. Calculer du travail du poids de l'échelle lors de cette opération.

 

$\begin{array}{rcl} W\left(\overrightarrow{P}\right)&=&-mg\dfrac{L}{2}&=&-10\times10\times\dfrac{3.0}{2}\\ &\Rightarrow&W\left(\overrightarrow{P}\right)\\

&=&-1.5\cdot10^{2}J \end{array}$

 

b. Calcul du travail du poids de l'échelle lors de cette opération.

 

$\begin{array}{rcl} W\left(\overrightarrow{P}\right)&=&-mg\dfrac{L}{2}\cos\alpha&=&-10\times10\times\dfrac{3.0}{2}\cos30^{\circ}\\ &\Rightarrow&w\left(\overrightarrow{P}\right)&=&-1.3\cdot10^{2}J \end{array}$

 

Exercice 10

 

 

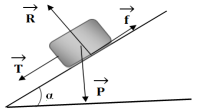
a. Bilan des forces extérieures s'appliquant à la caravane et représentation de ces forces

 

$\overrightarrow{T}$ : force de traction exercée par la voiture

 

$\overrightarrow{R}$ : réaction du plan incliné 

 

$\overrightarrow{f}$ : Force de frottement

 

$\overrightarrow{P}$ : poids de la caravane 

 

b. Résultante de ces forces

 

Le système évolue à vitesse constante, le principe de l'inertie s'écrit : 

 

$\overrightarrow{T}+\overrightarrow{P}+\overrightarrow{R}+\overrightarrow{f}=\overrightarrow{O}$

 

La résultante de ces forces est donc nulle

 

c. Calcul du travail du poids $\overrightarrow{P}$ et du travail de la force de frottement $\overrightarrow{f}$ pour un déplacement de longueur $L$

 

$\begin{array}{rcl} W\left(\overrightarrow{P}\right)&=&mgL\sin\alpha&=&500\times10\times200\times\dfrac{6.0}{100}&=&0\\ \RightarrowW\left(\overrightarrow{P}\right)&=&6\cdot10^{4}J \end{array}$

 

or

 

$\begin{array}{rcl} W\left(\overrightarrow{R}\right)&=&0\\ &\Rightarrow&W\left(\overrightarrow{T}\right)+W\left(\overrightarrow{P}\right)+W\left(\overrightarrow{f}\right)&=&0\\ &\Rightarrow&W\left(\overrightarrow{T}\right)&=&-W\left(\overrightarrow{P}\right)-W\left(\overrightarrow{f}\right)&=&-6\cdot10^{4}J-\left(-2.0\cdot10^{5}J\right)\\ &\Rightarrow&W\left(\overrightarrow{R}\right)=14\cdot10^{4}J \end{array}$

 

$\begin{array}{rcl} W\left(\overrightarrow{f}\right)&=&-fT&=&-1.0\cdot10^{3}\times200\\ &\Rightarrow&W\left(\overrightarrow{f}\right)\\ &=&-2.0\cdot10^{5}J \end{array}$

 

d. Déduction du travail de la force de la force de traction $\overrightarrow{T}$ exercée par la voiture sur la caravane 

 

$W\left(\overrightarrow{T}\right)+W\left(\overrightarrow{P}\right)+W\left(\overrightarrow{R}\right)+W\left(\overrightarrow{f}\right)=0$

 

La puissance moyenne de cette force

 

$\begin{array}{rcl} P_{m}\left(\overrightarrow{T}\right)&=&\overrightarrow{T}\overrightarrow{V}&=&TV\text{ or }T&=&\dfrac{W\left(\overrightarrow{T}\right)}{L}\\ &\Rightarrow&P_{m}\left(\overrightarrow{T}\right)&=&\dfrac{W\left(\overrightarrow{T}\right)}{L}V&=&\dfrac{14\cdot10^{4}}{200}\times19.4\\ &\Rightarrow&P_{m}\left(\overrightarrow{T}\right)\\ &=&1.36\cdot10^{2}W \end{array}$

 

e. La pente de la côte devrait être montante pour que le travail de $\overrightarrow{T}$ change de signe

 

La signification physique de ce changement de signe permet de préciser la nature du travail de $\overrightarrow{T}$