Espèce et variation - 2nd S
Classe:
Seconde s
Série:
S
Introduction
Le monde vivant renferme une grande diversité d'animaux et de végétaux qu'il faut identifier et placer dans des groupes plus ou moins homogènes.
C'est ainsi que les scientifiques ont défini des critères précis pour classer et nommer les différents êtres vivants.
Les êtres vivants issus d'un même parent ne se ressemblent souvent pas et ces différences sont traduites par le mot variation.
A. La notion l'espèce
I. Les critères d'identification d'une espèce
1. critères de ressemblance
a. Ressemblance morphologie
Les êtres vivants de la même espèce se ressemble entre eux plus qu'ils ne le sont avec ce d'une espèce voisine.
Ce critère a des limites
b. Ressemblance physiologique :
L'ascaris de l'homme ne pourrait vivre dans l'intestin du cheval et inversement.
Ces $2$ espèces sont morphologiquement identiques et pourtant ils ne sont pas de la même espèce car ils parasitent $2$ espèces différentes
c. Ressemblance chromosomique :
Les êtres vivant d'une même espèce possèdent normalement le même nombre et les mêmes formes de chromosomes exemple :
L'homme a $2n chr=46$
Ce critère connait des limites car des êtres vivants qui ne sont pas de la même espèce peuvent avoir le même nombre de chromosome.
Exemple le lion la panthère et le chat ont le même nombre de chromosome
$2n=38$
2. Critère d'interfécondite
Les individus de la même espèce se reproduisent entre eux et donnent des descendants fertiles.
Le brasage entre l'âne et la jument qui ne sont pas de la même espèce donne un hybride mâle (mulet) qui est stérile
3. Critère écologique
Pour que $2$ espèces se reproduisent elles doivent partager le même milieu écologique.
Exemple le cas des grimpereaux.
II. Définition de l'espèce
L'espèce peut être définie comme un ensemble d'être vivant qui se ressemblent morphologiquement, physiologiquement ayant le même nombre chromosomique, la même distribution écologique et pouvant se reproduire entre eux et dont leurs descendants sont fertiles.
B. La variation
I. Notion de variation
Les individus d'une même espèce ne sont jamais rigoureusement identiques.
Il existe entre eux un certains nombres de différence qui permettent de caractériser un individu au sein de sa population.
II. Définition de la variation
La variation traduit les différences des caractères c'est-à-dire des traits spécifiques, entre les individus qui constituent une espèce.
Notion de génome, de génotype et de phénotype
Chaque espèce est caractérisée par un ensemble d'information génétique qui constitue son patrimoine héréditaire.
Le gène est une portion de la molécule D'ADN qui gouverne un caractère.
Exemple le gène qui est responsable de la couleur des yeux.
Le génome d'une espèce correspond à l'ensemble des gènes de cette espèce.
Le génotype d'un individu indique les types d'allèles qui constituent chaque gène étudié de cet individu.
Le phénotype d'un individu correspond à l'ensemble des caractères apparents qui détermine l'identité de cet individu.
Le phénotype d'un individu dépend de son génotype et de son environnement.
1. Différents types de variation
a. Variation somatique (somation)
Ce sont des modifications (variation) lentes se développant progressivement sous l'action du milieu.
Ces modifications sont non héréditaires. Elles affectent le phénotype (caractère anatomique, morphologique, physiologique etc...) caractérisant un être vivant et non le génotype.
Ces modifications sont acquises au cours de la vie sous l'influence des facteurs du milieu.
b. Variation génétique (mutation)
Une mutation est une modification brusque d'un gène.
Elle donne naissance à un allèle nouveau.
Autrement dit la mutation est le processus de base par lequel un allèle naît d'un allèle, par modification d'un allèle préexistant.
Les mutations sont des modifications du phénotype dues à des modifications du génotype.
Les mutations se produisent, au hasard, n'importe quand et dans n'importe quelle cellule de l'organisme.
Les mutations somatiques sont individuelles alors que les mutations germinales sont héréditaires.
Les nouveaux allèles formés au cours de mutations somatiques disparaissent à la mort de l'organisme.
Seules peuvent se transmettre, au cours des générations futures, les nouveaux allèles formés à la suite de mutations germinales.
III. Étude statistique de la variation : la biométrie
C'est l'application des statistiques à la biologie
a. Analyse d'une distribution de fréquence
Le tableau de distribution de fréquence exprime le nombre de fois que chaque valeur, ou classe est rencontrée dans la population étudiée.
Autrement dit la fréquence de chaque classe dans la population.
Deux cas peuvent se présenter :
$\bullet\ $ou bien la variable est discontinue, c'est à-dire ne peut prendre que des valeurs déterminées qui se traduisent par des nombres entiers (nombre de graines, nombre de nervures etc.)
$\bullet\ $ou bien la variable est continue et dans ce cas le nombre de valeurs est infini et ces valeurs sont exprimées par des nombres décimaux (taille, poids etc.)
Exemple de série discontinue
Établissons le tableau de distribution de fréquence à partir des donnés d'une série discontinue.
Exemple de série continue
Arbitrairement choisissons des classes d'intervalle $4un$ , puis établissons le tableau de distribution de fréquence et déterminons la valeur centrale de chaque classe.
Les variables possibles étant infinies, elles sont regroupées en classes par des intervalles d'égale étendue, soit $4um$ par classe.
Chaque classe est définie par sa valeur centrale.
Le nombre de valeurs comprises dans la classe correspond à la fréquence de la classe.
Représentation graphique des résultats.
Pour traduire les résultats de manière simple et pratique, on utilise des représentations graphiques.
Il existe quatre types de représentation graphique.
b. Le digramme en bâton
On porte les classes en abscisse et en ordonnée les fréquences correspondantes.
Chaque classe est représentée à partir de sa valeur par un trait vertical ou bâton dont la hauteur correspond à sa fréquence.
Le diagramme en bâton est souvent utilisé pour représenter des séries discontinues.
Mais il est aussi utilisé pour des séries continues, chaque trait vertical aurait alors pour abscisse la valeur centrale de la classe qu'il représente.
c. Le polygone de fréquence
Il est tracé, soit à partir du diagramme en bâton, en reliant les sommets des bâtons par des segments de droites, soit à partir de l'histogramme de fréquence, en unissant les milieux des largeurs supérieures des rectangles par des segments de droites.
d. L'histogramme de fréquence
Il représente la variation continue ou discontinue par une série de rectangles de même largeur et dont les hauteurs sont proportionnelles aux fréquences des classes.
Chaque classe est représentée par un rectangle dont la base est la valeur de l'intervalle correspondant à la classe et la hauteur la fréquence de la classe.
1. Les paramètres caractéristiques d'une distribution de fréquence
Ces paramètres sont de deux catégories.
Les uns définissent la position et correspondent aux valeurs centrales autour desquelles sont réparties les variables ; les autres définissent la dispersion et permettent d'évaluer l'ampleur de la variation.
a. Les paramètres de position
On utilise ici le mode et la moyenne arithmétique
a. Le mode de la variation d'un caractère est la valeur de la classe qui correspond à la plus grande fréquence ; autrement dit la classe renfermant le plus grand nombre d'individus.
Ex : la classe $163.5-167.5$ pour la taille des paramécies.
La classe 11 pour le nombre de nervures.
$\bullet\ $La moyenne arithmétique :
C'est le rapport de la somme des variables fournies par les individus au nombre total d'individus.
Elle est donnée par la formule :
$\overline{X}=\dfrac{\Sigma f\bullet X}{\Sigma f}$
Pour les séries continues X= valeur centrale.
Remarque :
Si le polygone de fréquence est parfait le mode et la moyenne sont confondus.
b. Les paramètres de dispersion
Ces paramètres permettent d'évaluer l'amplitude de la variation.
On définit la dispersion à partir des écarts par à rapport la moyenne.
Plus les écarts seront petits plus la dispersion est faible.
$\bullet\ $La variance ou fluctuation : C'est la moyenne des carrés des écarts par rapport à la moyenne arithmétique.
Elle est exprimée par la formule :
$v=\dfrac{\Sigma f\left(X-\overline{X}\right)^{2}}{\sigma f}$
L'écart type :
C'est l'écart moyen par rapport à la moyenne arithmétique.
Il est exprimé par la formule :
$\delta=\sqrt{\dfrac{\Sigma f\left(X-\overline{X}\right)^{2}}{\Sigma f}}$
Tableau récapitulatif des chiffres permettant de calculer les paramètres de dispersion dans le cas des $271$ feuilles.
Voir annexe
$K=\dfrac{\delta\bullet 100}{\overline{X}}$
2. Interprétation des résultats de la biométrie
a. Interprétation des paramètres de dispersion.
$\bullet\ $Lorsque la variance et l'écart type ont des valeurs élevées cela signifie que le caractère est très variable ou fluctuant. On dit que la dispersion est forte.
$\bullet\ $Lorsque la variance et l'écart type ont des valeurs faibles cela signifie que le caractère est peu fluctuant.
On dit que la dispersion est faible la série est groupée ou apparemment homogène.
En somme lorsque la variance est supérieure à la moyenne, la dispersion est forte, la série est apparemment hétérogène.
Ce qui est le cas lorsque le coefficient de variabilité est supérieur à $30\%.$
Par contre si le coefficient de variabilité est inférieur $30\%$ ou la variance inférieure à la moyenne, la dispersion est faible, la série est apparemment homogène
b. Interprétation de polygones de fréquences
$\blacktriangleright$ Interprétation de polygone de fréquences uni modal.
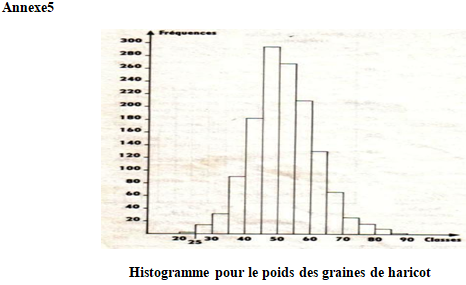
Le polygone de fréquence représentant la variation de poids des graines de haricot est uni modal avec un mode situé entre $46$ et $50.$
La population qu'elle représente serait apparemment homogène voir annexe-
$\blacktriangleright$Interprétation de polygone de fréquences bimodal.
Étudions maintenant la distribution de poids de fruits dans une population de tomates récoltée dans un champ.
La mesure des poids de chacun des fruits a permis de réaliser le polygone de fréquences suivant : voir annexe
Le polygone de fréquence présente deux modes : à la classe $95-105$ et à la classe $165-175.$
On parle de polygone bimodal, qui traduit une hétérogénéité de la population étudiée.
Chaque mode correspond à une valeur centrale caractéristique d'une race, c'est-à-dire une variété, aux caractères héréditaires, constitutive de l'espèce.
En somme le polygone bimodal représente une population hétérogène et le polygone uni modal une population apparemment homogène.
Cependant le polygone uni modal cache souvent une hétérogénéité que seule la sélection permet de déceler.
3. Application de la biométrie : cas de la sélection
La sélection consiste à opérer un choix au sein d'individus présentant des caractères précis ; les élus sont préservés par l'élimination des types ne possédant pas le caractère voulu, et par la pratique de l'auto-fécondation.
Choix, séparation, isolement, élimination sont à la base de la sélection.
Dans la nature, il existe une sélection naturelle, reposant sur une compétition vitale qui laisse survivre les individus les mieux adaptés aux conditions de vie.
Avec les graines de haricots, la sélection s'est révélée efficace, car elle a permis d'isoler deux types : un type lourd et un type léger.
En semant les graines lourdes $(36 – 90)$, les générations qui se suivent se ressemblent (poids oscillant entre 36 et 90 cg).
De ce fait les graines lourdes constituent une lignée pure, ou une race pure.
Il en est de même des graines légères.
Une lignée pure pour un caractère, est l'ensemble des individus ne présentant que ce caractère, et pouvant par conséquent transmettre que ce caractère.
Dans une lignée pure la sélection est inefficace
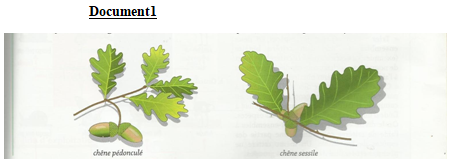
Consignes: observer attentivement ces $2$ photos
1. Ces photos sont-elles identiques morphologiquement ?
2. Peut-on dire que ces 2 espèces appartiennent à la même espèce ?
Document 2
L'ascaris de l'homme et du cheval sont morphologiquement identique mais ils ne parasitent pas la même hôte.
L’ascaris de l'homme ne peut pas vivre chez le cheval et inversement.

Consignes: lire le texte ci-dessus et observer attentivement ces $2$ photos.
1. Ces $2$ Ascaris appartiennent-elles à la même espèce et pourquoi?
2. Quel critère peut-on énoncer à partir de ces observations
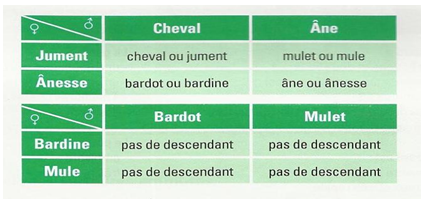
Consignes
Observer bien ces croisements entre cheval et ânesse d'une part et âne jument d'autre part
1. Quels sont les croisements qui donnent des descendants fertiles et ceux qui donnent des descendants infertiles ?
2. Ane et cheval sont de la même espèce et pourquoi ?
Document 4
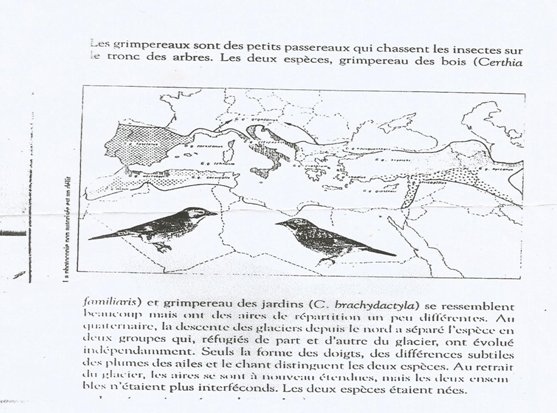
Consignes :
Lire attentivement le texte et observer bien le schéma.
1. Ces $2$ oiseaux se ressemblent-ils ?
2. Ont-ils la même répartition géographique
3. Ces $2$ oiseaux appartiennent-ils à la même espèce et pourquoi ?
Document 5 : Les organismes vivants présentent une structure
cellulaire : ils sont constitués de cellules.
Les cellules d'un organisme peuvent être catégorisées en deux groupes :
$\bullet\ $les cellules germinales ou cellules reproductrices, qui sont à l'origine des gamètes.
Elles constituent la lignée germinale ou le germen.
$\bullet\ $les cellules somatiques correspondent aux autres cellules, qui forment le corps ou soma. Elles constituent la lignée somatique.
Ces cellules renferment chacune un noyau, à l'intérieur duquel sont localisés les chromosomes.
Les chromosomes portent l'information génétique, les gênes
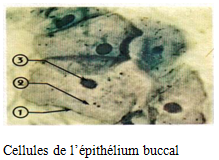
1. où se localise le gène et quel est son rôle? Comment appelle-t-on un ensemble de gêne?
2. Qu'est ce qui est à l'origine du caractère apparent d'un individu? Comment appelle-t-on ce caractère apparent.
Document 6 Les topinambours sont des plantes herbacées présentant des tubercules. Découpons en plusieurs portions, un tubercule de topinambour prélevé d'un pied.
Ces portions sont cultivées les unes en plaine, les autres en montagne


1. Comparez ces deux plants de Topinambours.
2. Que pouvez-vous dire du génotype de ces Topinambours.
3. Comment expliquez-vous ces phénotypes.
4. Définissez les notions de variation somatique.
Document 7
On rassemble les feuilles d'un arbrisseau, puis on compte le nombre de nervures de chaque feuille.
Pour $100$ feuilles examinées, on obtient les résultats suivants :

Le nombre de fois que la classe est rencontrée dans l'échantillon étudié constitue, la fréquence de la classe (nombre de feuilles ayant le même nombre de nervures)
Consignes Établir le tableau de distribution de fréquence sachant que chaque valeur du nombre de nervures trouvée constitue une classe $(5,6,7\ldots\ldots)$
Document 8
On mesure au micromètre prés la taille des différents individus d'une population de paramécies.
Les mesures suivantes sont trouvées

Consignes Les mesures trouvées peuvent être disposées en classes. Choisir arbitrairement des classes d'intervalle $4\,µm$, puis établir le tableau de distribution de fréquence et déterminer la valeur centrale de chaque classe.
Document 9
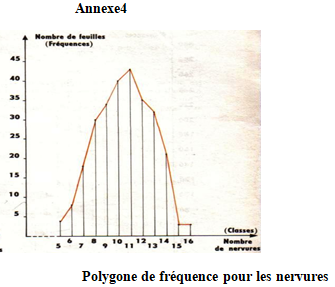
On a étudié la variation du nombre de nervures sur $271$ feuilles de baobab.
Voici le tableau de distribution de fréquences
$\begin{array}{|l|c|c|c|c|c|c|c|c|c|c|c|c|} \hline \text{Classes }&5&6&7&8&9&10&11&12&13&14&15&16\\ \hline \text{fréquences} &4&8&18&30&34&40&43&35&32&21&3&3\\ \hline \end{array}$
Consigne Tracer le diagramme en bâton
Document 10
Consigne Pour le même tableau de distribution de fréquence, tracer le polygone de fréquence (document 9)
Document 11
On a étudié variation de poids de graines de haricot de même espèce.
Voici le tableau de distribution de fréquences
$\begin{array}{|l|c|c|c|c|c|c|c|c|c|c|c|c|c|c|} \hline \text{Poids de }&21&26&31&36&41&46&51&56&61&66&71&76&81&86\\ \text{graines }&\text{à }&\text{ à }&\text{ à }&\text{ à }&\text{ à }&\text{ à }&\text{ à }&{ à }&\text{ à }&\text{ à }&\text{ à }&\text{ à }&\text{ à }&\text{ à}\\ (\text{en})cg&25&30&35&40&45&50&55&60&65&70&75&80&85&90\\ \hline \text{Fréquences }&2&14&32&89&182&293&267&209&130&66&26&17&9&1\\ \hline \end{array}$
Consigne Construire l'histogramme de fréquence
Document 12
Consigne Tracer la courbe de fréquence à partir du document 9
Document 13
La mesure des poids des fruits de tomate a permis de réaliser le polygone de fréquence ci-dessous.
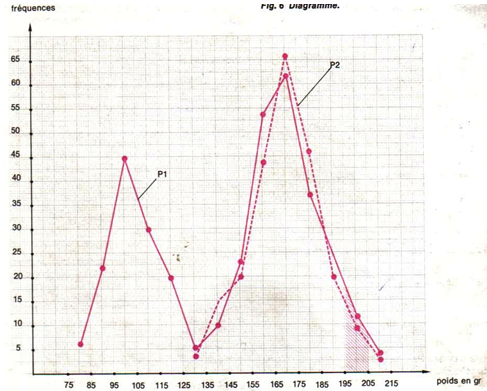
Consignes
1. Que représente ce graphe
2. Analyser et interpréter le graphe
3. Qu'est-ce qui le différencie avec le polygone de fréquence représentant la variation de poids des graines de haricot
4. Comment peut-on qualifier ce polygone
Annexe 1 Tableau de distribution de fréquences série discontinue
$\begin{array}{|l|c|c|c|c|c|c|c|c|c|c|c|c|} \hline \text{Classes }&&&&&&&&&&&&\\ \text{(nombre de nervures)}&5&6&7&8&9&10&11&12&12&14&15&16\\ \hline \text{Fréquences }&&&&&&&&&&&&\\ \text{(nombre de feuilles)}&1&2&4&8&14&17&20&15&10&6&2&1\\ \hline \end{array}$
Annexe 2 Tableau de distribution de fréquence série continue
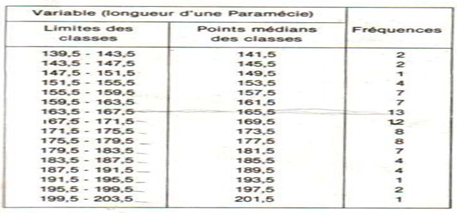
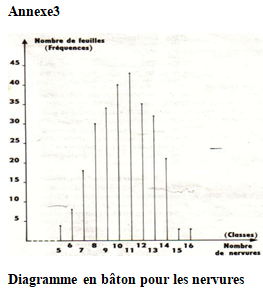
Diagramme en bâton pour les nervures
Polygone de fréquence pour les nervures

Ajouter un commentaire