Bac Maths C et E, Benin 2015

Assiba, étudiante en agronomie, a effectué un stage dans un Groupement Régional à Vocation Coopérative qui produit des huiles végétales. Plusieurs équipes de femme participe aux activités dont le stockage des huiles dans les cuves. si les $N$ femme de ce $GRVC$ se constituent en équipe de $6$ pour remplir les cuves, il en reste $4$ pour s'occuper des divers activités d'entretien. Mais pour qu'elles forment des équipes de $11$ en nombre  suffisant, elles ont recours aux services de $9$ stagiaires. Cette intégration des stagiaires aux équipes offre à Assiba l'occasion d'étudier l'évolution du bénéfice de la coopérative. Pour élaborer son rapport de stage, Assiba se fait aider de son jeune frère Gawé, élève en classe de terminale C, à qui elle confie la détermination de l'entier naturel $N(120<N<240)$, l'étude des caractéristiques des cuves, ainsi que l'évolution des bénéfices engrangées par le $GRVC.$

Tu es invité(e) à trouver une réponse aux préoccupations de Assiba en aidant Gawé à résoudre les trois problèmes suivant.

1. a) Justifie que $N$ vérifie le système
$$\left\lbrace\begin{array}{lcl} N&\equiv&4[6]\\ N&\equiv&2[11] \end{array}\right.$$

b) Déduis-en l'existence de deux entiers naturels $p$ et $q$ tels que : $N=6p+4$ et $11p−6q=2.$

2. a) Résous dans $\mathbb{Z^{2}}$ l'équation $11x−6y=2.$

b) Déduis-en la valeur de $N.$

c) Vérifie que $N$ s'écrit $\overline{262}$ en base $8.$

L'une des cuves servants à conserver l'huile a la forme d'un cylindre ayant à l'intérieur une partie tétraédrique $KOIJ$, une ouverture et deux robinets $R_{1}$ et $R_{2}.$ Le point $O$ est le centre du disque de base sur lequel repose le cylindre; le triangle $OIJ$ est isocèle et rectangle en $O$ ; le segment $[OK]$ est la hauteur du cylindre ; $OI=1\,m$ et $OK=2\,m$ :

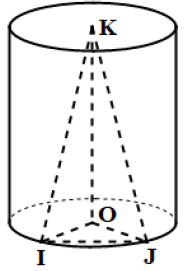
Le robinet $R_{1}$ est placé au point $A$ tel que : $\overrightarrow{OA}=\dfrac{1}{2}\overrightarrow{OI}+\dfrac{\sqrt{3}}{2}\overrightarrow{OJ}+\dfrac{1}{2}\overrightarrow{OK}.$

L'ouverture sur la base supérieure est délimitée par l'ensemble $(\Gamma)$ des points $M$ du plan rapporté au repère $(K\;,\ \overrightarrow{OI}\;,\ \overrightarrow{OJ})$ tels que : $2ME^{2}−4MF^{2}+2MG^{2}−4MH^{2}=-5$ avec $EFGH$ un carré de centre $K$ et $KG=1.$

Gawé munit l'espace du repère orthonormé direct $(O\;,\ \vec{i}\;,\ \vec{j}\;,\ \vec{k})$ tel que $\vec{i}=\overrightarrow{OI}\;,\ \vec{j}=\overrightarrow{OJ}\ \text{et}\ \vec{k}=\dfrac{1}{2}\overrightarrow{OK}$

3. Détermine les coordonnées du point $A.$

4. Le robinet $R_{2}$ est placé au point $B$, image du point $A$ par l'application $s_{1}\circ s_{2}$ où $s_{1}$ est la réflexion du plan $(KOI)$ et $s_{2}$ est la réflexion du plan $(KOJ).$

a) Justifie que $s_{1}\circ s_{2}$ est un demi-tour dont tu préciseras l'axe $(\Delta).$

b) Détermine les coordonnées du point $B.$

5. La partie tétraédrique contient un liquide de refroidissement et l'huile est stockée dans la partie restante du cylindre.

Calcule le volume d'huile qu'on peut stocker dans la cuve.

6. a) Justifie que $K$ est le barycentre des points pondérées $(E\;,\ 2)$ ; $(F\;,\ -4)$ ; $(G\;,\ 2)$ et $(H\;,\ -4).$

b) Détermine l'ensemble $(\Gamma).$

Une étude a permis de savoir qu'en fonction du nombre d'années $x$ d'existence de ce $GRVC$, le bénéfice réalisé en millions de franc $CFA$ est donné par : $f(x)=\mathrm{e}^{\dfrac{2x-1}{x}}-x$ avec $x>0.$

7. Démontre que $f$ admet un prolongement par continuité en $0.$

On note $g$ ce prolongement par continuité, et on note $(\mathcal{C})$ la courbe représentative de $g$ dans le plan muni du repère orthonormé $(O\;,\ \vec{i}\;,\ \vec{j}).$

8. a) Démontre que $g$ est continue sur $[0\ ;\ +\infty[.$

b) Étudie la dérivabilité de $g$ à droite en $0$ et donne une interprétation du résultat.

c) Calcule $g'(x)$ et $g''(x)$ pour $x$ élément de $[0\ ;\ +\infty[.$

9. a) Étudie le sens de variation de $g'$ sur $[0\ ;\ +\infty[.$

b) Démontre que $\lim\limits_{x\rightarrow 0^{+}}g'(x)=-1$

c) Dresse le tableau de variation de $g'.$

d) Démontre que l'équation $g'(x)=0$ admet deux solutions $\alpha$ et $\beta$ tels que : $$0.1<\alpha<0.2\quad\text{et}\quad 2.1<\beta<2.2.$$

e) Détermine le signe de $g'(x)$ pour tout $x$ élément de $]0\ ;\ +\infty[.$

10. a) Étudie les variations de $g.$

b) Démontre que $f(\alpha)=\alpha^{2}−\alpha\quad\text{et}\quad f(\beta)=\beta^{2}−\beta.$

Déduis-en un encadrement de chacun des nombres $f(\alpha)$ et $f(\beta).$

c) Trace la courbe $(\mathcal{C})$ sur l'intervalle $[0\ ;\ 7].$

11. Précise l'année au cour de laquelle la coopérative réalise son bénéfice maximum, ainsi que ce bénéfice.