Bac Maths D, Tunisie 2017

Exercice 1

L'espace est rapporté à un repère orthonormé direct $(O\;,\ \vec{i}\;,\ \vec{j}\;,\ \vec{k}).$

On considère les points $A(2\;,\ 2\;,\ 1)$, $B(0\,\ -2\;,\ 4)$ et $C(2\;,\ 0\;,\ -4 ).$

1. a) Déterminer les composantes du vecteur $\overrightarrow{OB}\wedge\overrightarrow{BC}.$

b) On note $\mathcal{P}$ le plan $(OBC).$

En remarquant que $\overrightarrow{OB}\wedge\overrightarrow{BC}=4\overrightarrow{OA}$, justifier que la droite $(OA)$ est perpendiculaire au plan $\mathcal{P}$ en $O.$

c) Montrer que la distance du point $O$ à la droite $(BC)$ est égale à $\sqrt{2}.$

2. Soit $(\mathcal{S})$ l'ensemble des points $M(x\ ;\ y\ ;\ z)$ de l'espace tels que : $$x^{2}+y^{2}+z^{2}-4x-4y-2z-2=0.$$

Montrer que $(\mathcal{S})$ est la sphère de centre $A$ et de rayon $\sqrt{11}.$

3. a) Calculer la distance $OA.$

b) En déduire que le plan $\mathcal{P}$ coupe la sphère $(\mathcal{S})$ suivant un cercle $(\mathcal{C})$ de centre $O$ et de rayon $\sqrt{2}.$

c) Montrer que la droite $(BC)$ est tangente au cercle $(\mathcal{C}).$

4. On considère le point $H(1\;,\ -1\;,\ 0).$

a) Montrer que $H$ est le point de contact de la droite $(BC)$ et du cercle $(\mathcal{C}).$

b) Détermine une équation cartésienne du plan $\mathcal{Q}$ tangente à $(\mathcal{S})$ en $H.$

Exercice 2

1. On considère dans $\mathbb{C}$ l'équation $(E)\ :\ z^{2}-(\sqrt{5}+2\mathrm{i})z+1+4\sqrt{5}\mathrm{i}=0.$

a) Calculer $(\sqrt{5}+2\mathrm{i})^{2}.$

b) Vérifier que le discriminant de l'équation $(E)$ est $\Delta=-3(\sqrt{5}+2\mathrm{i})^{2}.$

c) En déduire que les solutions de $(E)$ sont : $\alpha=(\sqrt{5}+2\mathrm{i})\left(\dfrac{1+\mathrm{i}\sqrt{3}}{2}\right)$ et

$\beta=(\sqrt{5}+2\mathrm{i})\left(\dfrac{1-\mathrm{i}\sqrt{3}}{2}\right).$

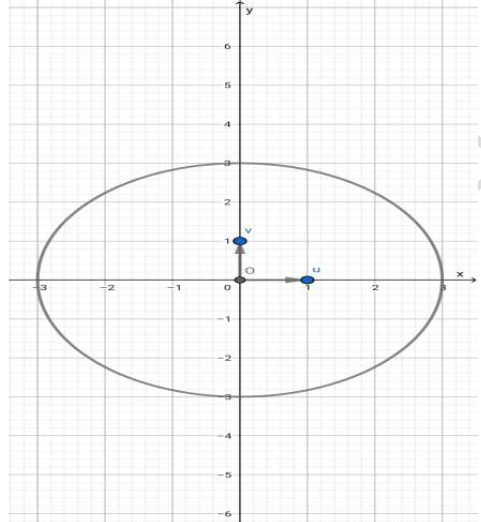
Dans la figure $1$ de l'annexe ci-jointe, $(O\;,\ \vec{u}\;,\ \vec{v})$ est un repère orthonormé direct du plan, $(\mathcal{C})$ est le cercle de centre $O$ et de rayon $3.$

2. Soit $Q$ le point d'affixe $\sqrt{5}+2\mathrm{i}.$

a) Montrer que le point $Q$ appartient à $(\mathcal{C}).$

b) Construire alors le point $Q.$

3. Soient $A$ et $B$ les points d'affixes respectives les nombres complexes $a$ et $b.$

a) Montrer que les points $A$ et $B$ appartiennent au cercle $(\mathcal{C}).$

b) Vérifier que $\overrightarrow{OA}+\overrightarrow{OB}=\overrightarrow{OQ}.$

c) En déduire que le quadrilatère $OAQB$ est un losange.

d) Construire alors les points $A$ et $B.$

Exercice 3

Soient $f$ la fonction définie sur $\mathbb{R}$ par $f(x)=(1+x^{2})\mathrm{e}^{-x}$ et $(\mathcal{C})$ sa courbe représentative dans un repère orthogonal $(O\;,\ \vec{i}\;,\ \vec{j}).$

1. a) Calculer $\lim\limits_{x\to -\infty}f(x).$

b) Montrer que $\lim\limits_{x\to -\infty}\dfrac{f(x)}{x}=-\infty$ et interpréter graphiquement le résultat.

c) Montrer que $\lim\limits_{x\to +\infty}f(x)=0$, et interpréter graphiquement le résultat.

2. a) Montrer que pour tout réel $x\;,\ f'(x)=−(x-1)2\mathrm{e}^{-x}.$

b) Dresser le tableau de variation de $f.$

3. a) Déterminer une équation cartésienne de la tangente à $(\mathcal{C})$ au point $J$ d'abscisse $0.$

b) Soient $A$ et $B$ les points de $(\mathcal{C})$ d'abscisse respectives $1$ et $3.$

Montrer que $A$ et $B$ sont deux points d'inflexion de $(\mathcal{C}).$

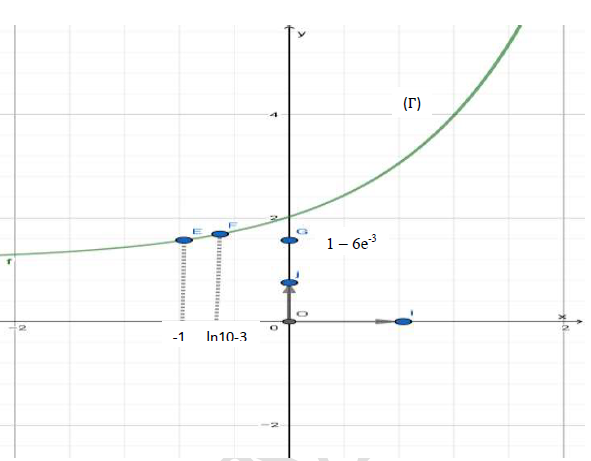
4. Dans la figure 2 de l'annexe ci-jointe :

$-\ (\Gamma)$ est la courbe représentative dans le repère $(O\;,\ \vec{i}\;,\ \vec{j})$ de la fonction $g$ définie sur $\mathbb{R}$ par $g(x)=\mathrm{e}^{x}.$

$-\ E$ et $F$ sont les points de $(\Gamma)$ d'abscisses respectives $(-1)$ et $\ln 10^{-3}.$

$-\ G$ est le point de coordonnées $(0\ ;\ 1\ - 6\mathrm{e}^{-3}).$

a) Exprimer $f(1)$ en fonction de $g(-1)$ et $f(3)$ en fonction de $g(3).$

b) En remarquant que $10g(-3)=g(\ln 10-3)$, placer les points $A$ et $B$ dans l'annexe.

5. a) Soit $K$ le point de coordonnées $\left(\dfrac{11}{2}\;,\ 0\right).$

Montrer que la droite $(BK)$ est la tangente à la courbe $(\mathcal{C})$ au point $B.$

b) Tracer la courbe $(\mathcal{C})$ dans l'annexe.

$($On placera les tangentes à $(\mathcal{C})$ en $A$, en $J$ et en $B).$

6. Soit $\mathcal{S}$ l'aire en $(u.a)$ de la partie $E$ du plan limitée par la courbe $(\mathcal{C})$, l'axe des abscisses et les droites d'équations cartésienne $x=0$ et $x=3.$

a) Hachurer $E.$

b) Soit $F$ la fonction définie sur $\mathbb{R}$ par $f(x)=−(x^{2}+2x+3)\mathrm{e}^{-x}.$

Montrer que $F$ est une primitive de $f$ sur $\mathbb{R}.$

c) Calculer $\mathcal{S}.$

d) Vérifier que la valeur moyenne de $f$ sur l'intervalle $[0\ ;\ 3]$ est à $1-6\mathrm{e}^{-3}.$

e) Tracer dans la figure 2 un rectangle d'aire égale à $\mathcal{S}.$

Exercice 4

Si une femme enceinte porte un seul fœtus, on dit qu'elle a une grossesse unique, sinon on dit qu'elle a une grossesse multiple. Dans une ville, une étude faite sur une population de femme enceinte montre que :

$\bullet\ $Le pourcentage des femmes ayant une grossesse multiple est de $5\%.$

$\bullet\ $Parmi les femmes ayant une grossesse multiple, $55\%$ finissent par accoucher dans le délai prévu.

$\bullet\ $Parmi les femmes ayant une grossesse unique, $92\%$ finissent par accoucher dans le délai prévu.

On choisit au hasard une femme de cette population. On désigne par $U$ et $D$ les évènements suivants : $U$ : « la femme a une grossesse unique ». $D$ : « la femme accouche dans le délai prévu ».

1. a) Déterminer $p(U).$

b) En utilisant les évènements $U$ et $D$, traduire en terme de probabilité les pourcentages $92\%$ et $55\%.$

2. a) Calculer $p(D).$

b) Une femme a accouché dans le délai prévu, montrer que la probabilité que sa grossesse soit unique est égale à $0.9694.$

3. Le service de maternité de cette ville prévoit qu'en Juillet $2017$, $n$ femmes enceintes devraient accoucher dans le délai prévu, $(n\geq 2).$

On note $p_{n}$ la probabilité qu'au moins une de ces femmes ait une grossesse multiple.

a) Exprimer $p_{n}$ en fonction de $n.$

b) Quel est le nombre minimal des femmes qui devront accoucher en Juillet $2017$ dans le délai prévu pour que la probabilité $p_{n}$ soit supérieur à $0.9$ ?