Bac Maths du 1er groupe S2 S4 S5 - 2018

 

1) On considère la fonction de répartition $F$ de la variable aléatoire $x$,

 

\begin{eqnarray} F\ :\ \mathbb{R}& \rightarrow &[0\;,\ 1]\nonumber\\ x& \mapsto &p(X\leq x)\nonumber \end{eqnarray} 

 

$p$ étant une probabilité définie sur un univers fini et non vide.

 

Dans un repère orthogonal, la représentation graphique de $F$ est la suivante :

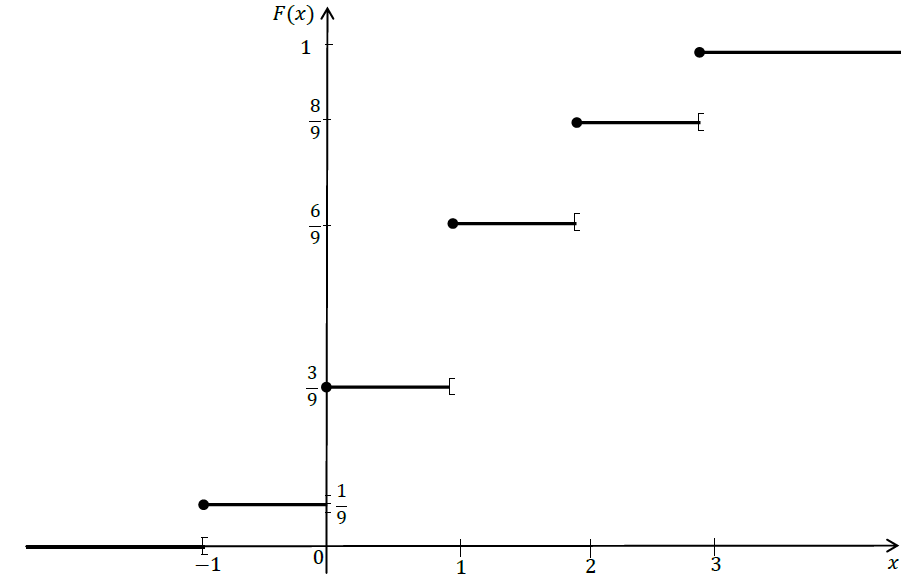
a) Déterminer $\lim_{x\rightarrow -\infty}F(x)$ et $\lim_{x\rightarrow +\infty}F(x).\quad(0.5\;pt)$

 

b) Déterminer la loi de probabilité de $X.\quad(1\;pt)$

 

c) Calculer les probabilités $p(X\leq 0)$ et $p(X\geq 1).\quad(0.5+0.5\;pt)$

 

d) Calculer l'espérance mathématique $E(X)$ de $X.\quad(0.5\;pt)$

 

e) Vérifier que l'écart type $\sigma(X)$ de $X$ est égal à $\dfrac{\sqrt{12}}{3}.\quad(0.5\;pt)$

 

2) On dispose de deux urnes $U_{1}$ et $U_{2}$ contenant chacune 3 boules. 

 

Les boules de $U_{1}$ sont numérotées respectivement $1\;,\ 2\;,\ 3$ et celles de $U_{2}$ portent respectivement les nombres $-2\;,\ -1\;,\ 0.$ 

 

On tire au hasard une boule de chaque urne et on effectue la somme $Y$ des numéros des boules tirées.

 

a) Dresser un tableau à double entrée permettant d'obtenir les valeurs possibles de $Y.\quad(0.75\;pt)$

 

b) En déduire que $X$ et $Y$ ont la même loi de probabilité.

1) Calculer $\left(\dfrac{\sqrt{2}}{2}+\dfrac{\sqrt{2}}{2}\mathrm{i}\right)^{2}.$

 

En déduire dans l'ensemble $\mathbb{C}$ des nombres complexes les solutions de l'équation $z^{2}-\mathrm{i}=0.\quad(0.25+0.5\;pt)$

 

2) On pose $P(z)=z^{3}+z^{2}-\mathrm{i}z-\mathrm{i}$ où $z$ est un nombre complexe.

 

a) Démontrer que l'équation $P(z)=0$ admet une solution réelle que l'on déterminera.$\quad(0.25\;pt)$

 

b) Résoudre l'équation $P(z)=0$ dans l'ensemble des nombres complexes.$\quad(0.5\;pt)$

 

3) Le plan est muni d'un repère orthonormé $(O\;,\ \vec{u}\;,\ \vec{v})$ d'unité graphique $2\;cm.$

 

On considère les points $A\;,\ B$ et $C$ d'affixes respectives $Z_{A}=\dfrac{\sqrt{2}}{2}(1+\mathrm{i})\;,\ z_{B}=\dfrac{-\sqrt{2}}{2}(1+\mathrm{i})\text{ et }Z_{C}=-1.$

 

a) Déterminer la forme exponentielle de $Z_{A}$ et celle de $Z_{B}.\quad(0.5\;pt)$

 

b) Placer avec précision les points $A\;,\ B$ et $C$ dans le plan complexe.$\quad(0.75\;pt)$

 

4) Soit $D$ le symétrique du point $A$ par rapport à l'axe réel.

 

a) Donner l'affixe $Z_{D}$ du point $D$ sous forme algébrique.$\quad(0.25\;pt)$

 

b) Démontrer que :

 

$\dfrac{z_{D}-z_{C}}{z_{A}-z_{C}}=\mathrm{e}^{-\mathrm{i}\frac{\pi}{4}}.$

 

En déduire la nature du triangle $ACD.\quad(0.25\times 2\;pt)$

 

5) Soit $E$ le point d'affixe $\dfrac{\sqrt{2}}{2}\mathrm{i}$ et $F$ sont symétrique par rapport à $O.$ 

 

On considère la similitude directe $S$ qui transforme $E$ en $A$ et $F$ en $B.$

 

a) Déterminer l'écriture complexe de $S$ et ses éléments caractéristiques.$\quad(0.25\times 4\;pt)$

 

b) Soit $(\mathcal{C})$ le cercle de centre $E$ et de rayon 1. 

 

Déterminer l'image $(\mathcal{C'})$ de $(\mathcal{C})$ par $S.\quad(0.5\;pt)$

Partie A

 

1) Soit l'équation différentielle $$(E)\ :\ y''+4y'+4y=0$$

 

Déterminer les solutions $h$ de $(E)$ définies sur $\mathbb{R}.\quad(0.5\;pt)$

 

2) On considère l'équation différentielle $$(F)\ :\ y''+4y'+4y=-4x$$

 

a) Déterminer les réels $a$ et $b$ tels que la fonction $\phi\ :\ x\mapsto ax+b$ soit solution de $(F).\quad(0.5\;pt)$

 

b) Montrer qu'une fonction $f$ est solution de $(F)$ si et seulement si $(f-\phi)$ est solution de $(E).\quad(0.75\;pt)$

 

c) En déduire toutes les solutions de $(F).\quad(0.5\;pt)$

 

d) Donner la solution $f$ de $(F)$ qui vérifie : $f(0)=2$ et $f'(0)=-2.\quad(0.5\;pt)$

 

Partie B
 

On considère la fonction $f$ définie sur l'intervalle $]-\infty\;;\ -1[\bigcup[0\;;\ +\infty[$ par :

$$f(x)=\left\lbrace\begin{array}{lcl} \ln\left(\dfrac{x+1}{x}\right)&\text{si}&x<-1\\ \\ x\mathrm{e}^{-2x}+\mathrm{e}^{-2x}-x+1&\text{si}&x\geq 0 \end{array}\right.$$

 

et $(\mathcal{C}_{f})$ sa courbe représentative dans un repère orthonormé $(O\;,\ \vec{i}\;,\ \vec{j})$ d'unité graphique $2\;cm.$

 

1) a) Calculer les dérivées $f'$ et $f''$ de la fonction $f$ sur $[0\;;\ +\infty[.\quad(1\;pt)$

 

b) Étudier les variations de $f'$, puis dresser le tableau de variation de $f'$ sur $[0\;;\ +\infty[.\quad(0.5+0.5\;pt)$

 

c) En déduire le signe de $f'$ sur $[0\;;\ +\infty[.\quad(0.5\;pt)$

 

2) Étudier les variations de $f$ sur $]-\infty\:;\ -1[.\quad(0.5\;pt)$

 

3) Dresser le tableau de variation de $f.\quad(0.5\;pt)$

 

4) Montrer que l'équation $f(x)=0$ admet une solution unique $\alpha$ et que $1\leq\alpha\leq 2.\quad(0.5+0.5\;pt)$

 

5) Montrer que la courbe $(\mathcal{C}_{f})$ admet une asymptote oblique $(\mathcal{D})$ que l'on déterminera, puis étudier la position de $(\mathcal{D})$ par rapport à la courbe $(\mathcal{C}_{f}).\quad(0.5+0.5\;pt)$

 

6) Construire les asymptotes, puis la courbe $(\mathcal{C}_{f}).$