Vous êtes ici

Bac Physique chimie 1er Groupe S2 S2A S4 S5 2007

Exercice 1 (04.5 points)

Les alcools sont présents dans la nature, ils entrent dans la constitution de divers organes végétaux et animaux.

Ils sont d'une importance toute particulière dans le monde industriel avec la préparation de détergents et autres composés tensioactifs.

Au laboratoire, ils sont principalement utilisés comme solvants et comme intermédiaires de synthèse.

Aldéhydes, cétones, acides carboxyliques, esters... autant de composés qui peuvent être obtenus des alcools.

1.1 Au cours d'une séance de travaux pratiques on veut identifier trois alcools notés $A$, $B$ et $C.$

On donne trois formules moléculaires brutes $C_{2}H_{6}O$ ; $C_{3}H_{8}O$ et $C_{4}H_{10}O.$

Chacune de ces formules peut être celle de l'alcool $A$, de l'alcool $B$ ou de l'alcool $C.$

Pour identifier ces alcools on a réalisé les tests suivants :

$\bullet$ Premier test :

On fait l'oxydation ménagée des alcools à l'aide du dichromate de potassium en milieu acide et on constate que :

- $A$ ne donne pas de réaction.

- $B$ et $C$ réagissent pour donner respectivement les produits organiques $B'$ et $C'.$

$\bullet$ Deuxième test :

Les produits $B'$ et $C'$ donnent avec la dinitrophénylhydrazine (DNPH) un précipite jaune ; mais seul $B'$ rosit le réactif de Schiff.

1.1.1 Donner, en justifiant, les fonctions chimiques de $B'$ et $C'$ (0.50 point)

1.1.2 En déduire les classes des alcools $A$, $B$ et $C.$ (0.75 point)

1.1.3 Identifier les alcools en donnant leurs formules semi-développées et leurs noms. (0.75 point)

1.1.4 Écrire les demi-équations électroniques des couples $B'/B$ et $Cr_{2}O_{7}^{2-}/Cr^{3+}$ puis l'équation-bilan de la réaction de $B$ avec l'ion dichromate. (0.75 point)

1.2 On étudie ensuite la cinétique de la réaction entre l'acide éthanoïque et l'alcool $C_{2}H_{6}O.$

On réalise un mélange contenant $1$ mole d'alcool et $1$ mole d'acide et quelques gouttes d'acide sulfurique concentré.

Le mélange est réparti dans $10$ tubes à essais que l'on place ensuite dans un

bain-marie à la température de $100^{\circ}C.$

A une date $t$, on prend un tube que l'on place dans de l'eau glacée et le contenu est dosé par une solution d'hydroxyde de sodium de concentration connue afin de déterminer le nombre $n_{ac}$ de mole d'acide restant.

1.2.1 Trouver dans le protocole expérimental les moyens utilisés pour augmenter la vitesse de la réaction. (0.25 point)

1.2.2 Pourquoi utilise-t-on l'eau glacée ? (0.25 point)

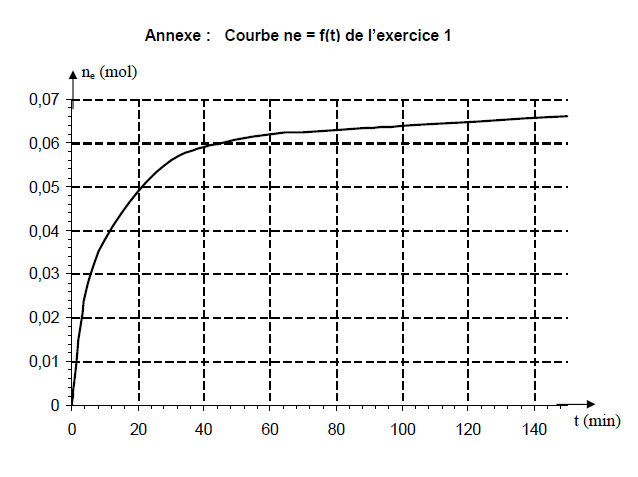
1.2.3 La connaissance de la quantité de matière $n_{ac}$ d'acide restant a permis de déterminer la quantité de matière $n_{e}$ d'ester formé au cours du temps et par suite de tracer la courbe d'estérification $n_{r}=f(t)$ jointe en annexe (page 4).

a) Définir la vitesse instantanée de formation de l'ester. (0.25 point)

b) Déterminer cette vitesse à $t=20\,min$ puis à $t=80\,min.$

Comment évolue la vitesse au cours du temps ?

Pourquoi ? (01 point)

Exercice 2 (03.5 points)

Les protéines participent au fonctionnement des organismes vivants, de l'être humain en particulier, en intervenant dans un grand nombre de réactions biochimiques d'importance capitale.

Ce sont des macromolécules de natures diverses ; et pourtant elles ne sont constituées qu'à partir d'une vingtaine de maillons élémentaires : les acides $\alpha$-aminés.

Le nombre et l'ordre dans lesquels ces maillons sont liés caractérisent ces protéines.

2.1 Dans ce qui suit on considère les acides $\alpha$-aminés de formule brute $C_{6}H_{13}O_{2}N.$

L'un de ces acides $\alpha$-aminés, l'acide $2$-amino-$3$-méthylpentanoïque, usuellement appelé isoleucine, possède deux carbones asymétriques.

2.1.1 Écrire la formule semi-développée de l'isoleucine et marquer d'une croix chaque carbone asymétrique. (0.50 point).

2.1.2 Écrire les formules semi-développées et donner les noms de trois acides $\alpha$-aminés isomères de l'isoleucine. (01.5 point).

2.2 En solution aqueuse, l'isoleucine donne un ion dipolaire appelé zwittérion qui coexiste avec un cation et un anion en des proportions différentes selon le pH de la solution.

Écrire les équations des deux réactions du zwittérion sur l'eau.

Attribuer aux couples acide-base du zwittérion les valeurs de $pKA$ : $pK_{1}=2.2$ et $pK_{2}=9.6.$

Quelle est l'espèce prépondérante dans le duodénum où le $pH$ est voisin de $7.4$ ? (0.50 point)

2.3 On réalise une réaction de condensation entre l'isoleucine et la glycine de formule $H_{2}N\ -\ CH_{2}\ -\ CO_{2}H.$

2.3.1 Montrer que cette réaction de condensation conduit à deux dipeptides isomères $P_{1}$ et $P_{2}.$

Donner leur formule semi-développée en mettant en évidence la liaison peptidique. (0.50 point)

2.3.2 On désire synthétiser un des dipeptides $P_{1}$ ou $P_{2}.$

Décrire le principe de la synthèse. (0.50 point)

Exercice 3 (04.5 points)

En travaux pratiques un groupe d'élèves utilisent deux méthodes différentes pour déterminer la constante de raideur $K$ d'un ressort à spires non jointives.

$\bullet$ 3.1. La méthode statique :

L'extrémité supérieure du ressort est fixée.

A son extrémité libre, sont suspendues successivement des masses de différentes valeurs (figure a).

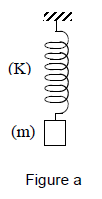
Pour chaque masse $m$ l'allongement $\Delta\ell$ du ressort est mesuré à l'aide d'une règle (non représentée sur la figure).

Le tableau de valeurs suivant est obtenu :

$$\begin{array}{|c|c|c|c|c|c|c|c|c|} \hline m(kg)&0.1&0.2&0.3&0.4&0.5&0.6&0.7&0.8\\ \hline \Delta\ell(cm)&2.5&5.0&7.5&10&12.4&15.1&17.5&19.8\\ \hline \end{array}$$

3.1.1 Tracer le graphe de l'allongement $\Delta\ell$ en fonction de la masse $m.$

En déduire la relation numérique entre $\Delta\ell$ et $m.$ (0.75 point)

3.1.2 Sur un schéma, représenter les forces s'exerçant sur la masse $m.$

Traduire alors la condition d'équilibre et en déduire l'expression de $K$ en fonction de $m$, $\Delta\ell$ et l'intensité de la pesanteur $g.$ (0.75 point).

3.1.3 En déduire la valeur de la constante de raideur $K.$

On prendra $g=9.81\,m\cdot s^{-2}.$ (0.50 point)

$\bullet$ 3.2. La méthode dynamique :

Dans cette partie le ressort précédent est utilisé pour réaliser un oscillateur horizontal.

Le solide de masse $M$, de valeur inconnue, solidairement lié au ressort, se déplace sur un support horizontal (figure b).

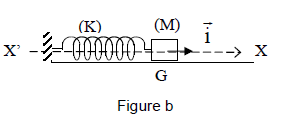
Tous les frottements sont négligés.

On utilise un axe $X'X$ horizontal orienté par le vecteur unitaire $\vec{i}$ et on repère la position du centre d'inertie $G$ du solide par son abscisse $X$ sur cet axe.

A l'équilibre le ressort n'est ni comprimé, ni allongé et l'abscisse $X$ est nulle (le point $G$ est confondu avec l'origine de l'axe $X'X).$

A un instant choisi comme origine des temps, la masse est écartée de sa position d'équilibre, et lâchée sans vitesse initiale.

3.2.1 Faire l'inventaire des forces qui s'exercent sur la masse $M$ à un instant $t$ donné et les représenter sur un schéma. (0.50 point)

3.2.2 Par application du théorème du centre d'inertie appelé aussi deuxième loi de Newton, établir l'équation différentielle du mouvement.

En déduire l'expression de la période $T_{0}$ des oscillations en fonction de la constante de raideur $K$ et de $M.$ (0.50 point)

3.2.3 La mesure de $10$ oscillations donne $10.6\,s.$

Calculer $T_{0}.$ (0.25 point)

3.2.4 L'objet précédent de masse $M$ est surchargé d'une masse $m_{1}=20\,g$ fixée sur lui.

Le système est à nouveau mis en oscillation comme précédemment.

Cette fois la durée de $10$ oscillations donne $10.7\,s.$

Exprimer la nouvelle période $T$ en fonction de $K$, $m_{1}$ et $M.$ (0.25 point)

3.2.5 En déduire l'expression de $K$ en fonction de $T_{0}$, $T$ et $m_{1}.$ (0.50 point)

3.2.6 Calculer $K.$

Comparer avec le résultat obtenu par la méthode statique.

Expliquer. (0.50 point)

Exercice 4 (04 points)

4.1 On réalise une expérience d'interférences en lumière monochromatique de longueur d'onde $\gamma.$

On utilise pour cela une fente source horizontale avec laquelle on éclaire deux fentes horizontales très fines $F_{1}$ et $F_{2}$ distantes de $a=200\mu m$ et situées à égale distance de la source.

A la distance $D=1\,m$ des fentes $F_{1}$ et $F_{2}$ on place un écran qui leur est parallèle et qui permet d'observer le phénomène d'interférences.

On considère sur l'écran un axe $Ox$ vertical, le point $O$ se trouvant dans le plan médiateur des fentes $F_{1}$ et $F_{2}.$

4.1.1 Décrire et expliquer qualitativement l'aspect de l'écran. (0.25 point)

4.1.2 Pourquoi utilise-t-on une fente source avant les fentes $F_{1}$ et $F_{2}$ ? (0.25 point)

4.1.3 Établir pour un point $M$ de l'axe $Ox$ d'abscisse $x$, la différence de marche $\delta$ entre les rayons provenant de $F_{1}$ et $F_{2}.$ (0.50 point)

4.1.4 Exprimer en fonction de $\gamma$, $D$, $a$ et de l'entier $k$, l'abscisse d'un point de l'écran appartenant à une frange sombre et en déduire l'expression de l'interfrange $i.$ (0.50 point)

4.1.5 On mesure $i=2.74\,mm.$

Quelle est la longueur d'onde de la lumière utilisée ? (0.25 point)

4.2 On utilise maintenant des filtres permettant de sélectionner différentes radiations monochromatiques.

Pour chaque radiation, on mesure la distance correspondant à sept $(7)$ interfranges et on consigne les résultats obtenus dans le tableau suivant :

$$\begin{array}{|c|c|c|c|c|c|} \hline \gamma(\mu m)&0.470&0.520&0.580&0.610&0.650\\ \hline 7\,i(mm)&16.5&18.2&20.3&21.4&22.8\\ \hline i& & & & &\\ \hline \end{array}$$

4.2.1 Pourquoi mesure-t-on la distance correspondant à $7$ interfranges plutôt que celle de l'interfrange $i$ ? (0.25 point)

4.2.2 Compléter le tableau puis tracer la courbe représentative de la fonction $i=f(\gamma).$ (0.50 point)

Échelle : $1\,cm\rightarrow 0.05\mu m$ en abscisses ;

$1\,cm\rightarrow 0.2\,mm$ en ordonnées

4.2.3 L'expression de l'interfrange établie à la question 4.1.4 est elle en accord avec la courbe obtenue ?

Justifier. (0.25 point)

4.2.4 A partir de la courbe, c'est-à-dire graphiquement, déterminer :

a) L'interfrange obtenue à partir d'une radiation de longueur d'onde $\gamma_{1}=0.600\mu m.$ (0.25 point)

b) La longueur d'onde donnant un interfrange $i_{2}=2.5\,mm.$ (0.25 point)

4.3 On opère maintenant en lumière blanche.

4.3.1 Décrire sommairement l'aspect de l'écran. (0.25 point)

4.3.2 On place dans le plan de l'écran, parallèlement aux fentes $F_{1}$ et $F_{2}$, la fente d'un spectroscope à $12\,mm$ du point $O.$

Calculer le nombre de radiations manquantes et les longueurs d'ondes correspondantes.

Les limites du spectre visible sont $0.4\mu m$ et $0.8\mu m.$ (0.50 point)

Exercice 5 (03.5 points)

Une bobine circulaire $PQ$ de résistance $R_{2}=8$ ohms comportant $N_{2}=50$ spires de diamètre $d_{2}=5\,cm$ est placée comme indiqué sur la figure à l'intérieur d'un solénoïde de longueur $\ell_{1}=50\,cm$, comportant $N_{1}=1000$ spires.

L'axe de la bobine est parallèle à celui du solénoïde.

5.1 Un générateur de courant continu débite un courant d'intensité $I=4A$ à travers le solénoïde.

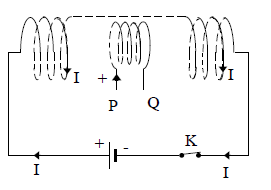
Déterminer alors les caractéristiques du champ magnétique $\overrightarrow{B}$ créé à l'intérieur du solénoïde et représenter ce vecteur sur un schéma. (01 point)

On donne : perméabilité du vide : $\mu_{0}=4\pi\cdot 10^{-7}$ SI

5.2 Sans modifier le circuit, on réunit les extrémités $P$ et $Q$ de la bobine, puis on ouvre l'interrupteur $K.$

5.2.1 Justifier le passage d'un courant induit dans la bobine $PQ$ pendant l'ouverture du circuit et préciser son sens sur un schéma (le sens positif d'orientation de $PQ$ est indiqué sur le schéma du montage). (0.75 point)

5.2.2 Calculer la quantité d'électricité induite qui traverse la bobine $PQ.$ (0.50 point)

5.3 Le générateur linéaire est remplacé par un générateur basse fréquence qui délire une intensité variable $i=5\sin(100\pi)t$, expression où $i$ est exprimée en ampère et $t$ en seconde.

5.3.1 Montrer que l'expression de la f.e.m d'induction qui apparaît dans la bobine est $e=-\dfrac{\mu_{0}N_{1}N_{2}\ \pi\mathrm{d}_{2}^{2}}{4\ell_{1}}\dfrac{\mathrm{d}i}{\mathrm{d}t}$, relation où $\dfrac{\mathrm{d}i}{\mathrm{d}t}$ est la dérivée par rapport au temps de l'intensité $i$ du courant (0.50 point)

5.3.2 On sépare les bornes $P$ et $Q$ de la bobine puis on relie la borne $Q$ à la masse d'un oscilloscope, la borne $P$ à la voie de déviation verticale $YY'$ afin de visualiser la tension $U_{PQ}.$

Représenter la courbe observée sur l'écran en tenant compte des données ci-dessous : (0.75 point)

- largeur de l'écran : $10\,cm$ balayage horizontal : $5\,ms/cm$

- hauteur de l'écran : $08\,cm$ sensibilité verticale : $0.2\,V/cm.$

Commentaires

Diop (non vérifié)

mer, 04/08/2020 - 03:04