Corrigé Bac Maths S2 2e groupe 2015

1) a) Ensemble de définition de $f$

 

Pour plus de clarté, nous reproduisons la courbe de $f.$

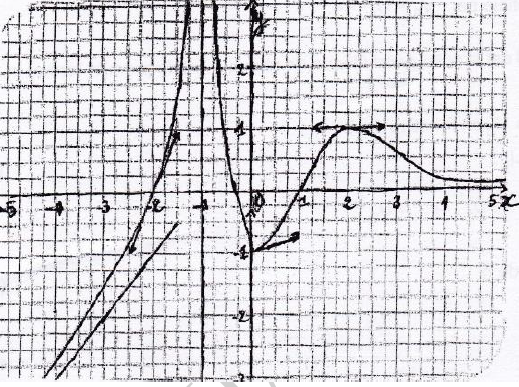
Au vu de cette figure, il apparaît que toute droite "verticale" (c'est-à-dire parallèle à l'axe des $y)$ coupe la courbe $(C_{f})$ en un unique point, sauf la droite d'équation $x=-1.$ On peut donc considérer que $f$ est définie partout sur $\mathbb{R}$ sauf en $x_{0}=-1.$ Par conséquent, $$D_{f}=\mathbb{R}\setminus\{-1\}=]-\infty\;,\ -1[\cup]-1\;,\ +\infty[$$

 

2) Lecture graphique de certaines limites

• $\lim_{x\rightarrow -\infty}f(x)=-\infty$ car quand on regarde vers le côté gauche du dessin, c'est-à-dire les points de $(C_{f})$ pour des valeurs négatives de la variable $x$, la courbe semble se diriger vers le bas autrement dit les valeurs correspondantes de $f(x)$ deviennent de plus en plus grandes en valeur absolue mais négatives.

 

• $\lim_{x\rightarrow +\infty}f(x)=0$ car quand on regarde vers le côté droit du dessin, c'est-à-dire les points de $(C_{f})$ pour des valeurs de plus en plus grandes de la variable $x$, la courbe semble se rapprocher indéfiniment de l'axe des abscisses.

 

• $\lim_{x\rightarrow -1}f(x)=+\infty$ (en fait on a $\lim_{x\rightarrow -1+}f(x)=+\infty$ et $\lim_{x\rightarrow -1^{-}}f(x)=+\infty$) car quand on considère les points de la courbe dont les abscisses sont proches de 1, qu'elles soient inférieures ou supérieures à 1, on constate que leurs ordonnées deviennent de plus en plus grandes et positives (la courbe semble se diriger vers le haut).

 

• $\lim_{x\rightarrow +\infty}\dfrac{x}{f(x)}=+\infty$ car quand $x$ tend vers $+\infty$, on a évidemment $x\rightarrow +\infty$ mais $f(x)\rightarrow 0^{+}$, d'où le résultat d'après les théorèmes généraux sur la limite d'un quotient.

 

• $\lim_{x\rightarrow -\infty}f\left(\dfrac{3}{x^{2}}\right)=-1$ car $\lim_{x\rightarrow -\infty}\left(\dfrac{3}{x^{2}}\right)=0$ et $\lim_{x\rightarrow 0}f(x)=-1$ d'où le résultat par composition des limites.

 

• $\lim_{x\rightarrow 0^{-}}\dfrac{f(x)+1}{x}=-\infty$; en effet, cette limite est celle du taux de variation de $f$ en 0 par valeurs inférieures et l'examen de la courbe montre que $(C_{f})$ admet une demi-tangente verticale dirigée vers le haut à gauche de 0.

 

c) Nature des branches infinies de $(C_{f})$

 

• Au voisinage de $-\infty\;,\ (C_{f})$ admet d'après la figure une asymptote oblique $(\Delta).$ Pour déterminer une équation de $(\Delta)$, on cherche les coordonnées de deux points par lesquelles elle passe. En examinant la figure, on voit que $(\Delta)$ passe (bien regarder et compter les carreaux, la figure de l'énoncé étant malheureusement de mauvaise qualité) par $A\begin{pmatrix} -2\\ -1 \end{pmatrix}$ et $B\begin{pmatrix} -3\\ -2 \end{pmatrix}$. Son équation est de la forme $y=ax+b$ avec $a=\dfrac{-2-(-1)}{-3-(-2)}=\dfrac{-1}{-1}=1$ et puisque $A\in(\Delta)$, ses coordonnées vérifient l'équation de $(\Delta)$, d'où $-1=a\times(-2)+b=1\times(-2)+b$, et par conséquent $b=1.$ 

 

$(\Delta)$ a donc pour équation $y=x+1.$

 

• La droite d'équation $x=-1$ est asymptote verticale à $(C_{f})$ car 

 

$\lim_{x\rightarrow -1}f(x)=+\infty$

 

• La droite d'équation $y=0$ est asymptote horizontale à $(C_{f})$ car 

 

$\lim_{x\rightarrow +\infty}f(x)=0$

 

d) Résolution graphique de l'équation $f(x)=0$

 

Ce sont les abscisses des points où la courbe intersecte l'axe des abscisses. Par lecture, on trouve : $$S=\left\{-2\;;\ -\dfrac{1}{4}\;;\ 1\right\}$$

 

2) Lecture graphique de nombres-dérivés

 

• En regardant attentivement le quadrillage, on voit que le vecteur directeur de la tangente au point d'abscisse -2 a pour coordonnées (par exemple) $\begin{pmatrix} \dfrac{1}{2}\\ \\ 1 \end{pmatrix}$, ou encore $\begin{pmatrix} 1\\ 2 \end{pmatrix}.$ Donc $f'(-2)=2.$

 

• On a $f'(2)=0$ car au point d'abscisse 2, la tangente est horizontale.

 

• $f'_{d}(0)=\dfrac{1}{4}$ car la demi-tangente à gauche en 0 a un vecteur directeur de coordonnées $\begin{pmatrix} 1\\ \\ \dfrac{1}{4} \end{pmatrix}.$

 

3) Tableau de variation de $f$

 

Il découle de la figure. On voit clairement que $f$ est croissante sur $]-\infty\;;\ -1[$, décroissante sur $]-1\;;\ 0]$, croissante sur $[0\;;\ 2]$ et décroissante sur $[2\;;\ +\infty[.$

 

$$\begin{array}{|c|lcccccccr|} \hline x&-\infty& &-1& &0& &2& &+\infty \\ \hline f'(x)& &+&||&-&||&+&|&-& \\ \hline & & &+\infty& & & &1& & \\ f& &\nearrow&||&\searrow& &\nearrow& &\searrow& \\ &-\infty& &||& &-1& & & &0 \\ \hline\end{array}$$

Étude de la suite $(U_{n})$ définie par : $\left\lbrace\begin{array}{rcl} U_{0} &=& 0\\ \\ U_{n+1} &=& \dfrac{1}{2}\sqrt{U_{n}^{2}+12} \end{array}\right.$

 

1) Calcul $U_{1}$ et $U_{2}$

 

On a, en remplaçant $n$ par 0 dans la relation de récurrence définissant la suite :

$$U_{1}=\dfrac{1}{2}\sqrt{U_{0}^{2}+12}=\dfrac{\sqrt{12}}{2}=\sqrt{3}\quad\text{et}\quad U_{2}=\dfrac{1}{2}\sqrt{U_{1}^{2}+12}=\dfrac{\sqrt{15}}{2}$$

 

2) Étude de la suite auxiliaire $(V_{n})$ définie par : $V_{n}=U_{n}^{2}-4$ 

 

a) Nature et éléments caractéristiques de $(V_{n})$

 

On a successivement :

$\begin{array}{rcl} V_{n+1}&=&U_{n+1}^{2}-4 \\ &=&\dfrac{1}{4}\left(U_{n}^{2}+12\right)-4\\&=&\dfrac{U_{n}^{2}}{4}+3-4\\&=&\dfrac{U_{n}^{2}}{4}-1\\&=&\dfrac{U_{n}^{2}-4}{4}\end{array}$

 

Soit $V_{n+1}=\dfrac{1}{4}\left(U_{n}^{2}-4\right)=\dfrac{1}{4}V_{n}$

 

Il en résulte que la suite $(V_{n})$ est une suite géométrique de raison $\dfrac{1}{4}$ et de premier terme $V_{0}=U_{0}^{2}-4=-4.$

 

b) Expression de $V_{n}$ , puis de $U_{n}$ en fonction de $n$ et limite de la suite $(U_{n}).$

 

Les formules relatives aux suites géométriques donnent alors :

 

$V_{n}=V_{0}q^{n}=-4\times\left(\dfrac{1}{4}\right)^{n}=-\left(\dfrac{1}{4}\right)^{n-1}$ (simplification par 4), puis :  $U_{n}^{2}=V_{n}+4$, soit puisque la suite $(U_{n})$ est visiblement à termes positifs (on peut le montrer très simplement par récurrence),

$\begin{array}{rcl} U_{n}&=&\sqrt{V_{n}^{2}+4}\\&=&\sqrt{-\left(\dfrac{1}{4}\right)^{n-1}+4}\\&=&\sqrt{4\left[1-\left(\dfrac{1}{4}\right)^{n}\right]}\\&=&2\sqrt{1-\left(\dfrac{1}{4}\right)^{n}}\end{array}$

 

Puisque $\dfrac{1}{4}$ est compris entre 0 et 1 (donc appartient à $]-1\;;\ 1[$), on a :

 

$\lim_{n\rightarrow +\infty}\left(\dfrac{1}{4}\right)^{n}=0$ et par conséquent $\lim_{n\rightarrow +\infty}U_{n}=2$

 

3) Calcul de $S_{n}=U_{0}^{2}+U_{1}^{2}+\cdots+U_{n}^{2}$ et de $\lim_{n\rightarrow +\infty}\dfrac{S_{n}}{n}$

 

En sommant membre à membre les $(n+1)$ égalités :

$\begin{array}{rcl} V_{n}&=&U_{n}^{2}-4\\ V_{n-1}&=&U_{n-1}^{2}-4\\ \cdots &\cdots&\\ \cdots&\cdots&\\ \cdots&\cdots&\\ V_{0}&=&U_{0}^{2}-4\end{array}$

 

On obtient $\sum_{i=0}^{i=n}V_{i}=\sum_{i=0}^{i=n}U_{i}^{2}-4(n+1).$

 

Or d'après la formule relative à la somme des termes d'une suite géométrique, on a :

$\begin{array}{rcl} \sum_{i=0}^{i=n}V_{i}&=&-4\times\dfrac{1-\left(\dfrac{1}{4}\right)^{n+1}}{1-\dfrac{1}{4}} \\&=&\sum_{i=0}^{i=n}U_{i}^{2}-4(n+1)\end{array}$

 

D'où 

$\begin{array}{rcl} \sum_{i=0}^{i=n}U_{i}^{2}&=&4\left[(n+1)-\dfrac{4}{3}\left[1-\left(\dfrac{1}{4}\right)^{n+1}\right]\right] \\ &=&4\left[n-\dfrac{1}{3}+\dfrac{4}{3}\left(\dfrac{1}{4}\right)^{n+1}\right]\end{array}$

 

Soit $$S_{n}=4\left[n-\dfrac{1}{3}+\dfrac{1}{3}\left(\dfrac{1}{4}\right)^{n}\right]$$

 

Il en résulte que $\dfrac{S_{n}}{n}=4\left[1-\dfrac{1}{3n}+\dfrac{1}{3n}\left(\dfrac{1}{4}\right)^{n}\right].$

 

Des relations $\lim_{n\rightarrow +\infty}\left(\dfrac{1}{3n}\right)=0$ et $\lim_{n\rightarrow +\infty}\left(\dfrac{1}{4}\right)^{n}=0$, et des opérations sur les limites de suites, il découle alors que : $$\lim_{n\rightarrow +\infty}\dfrac{S_{n}}{n}=4$$

1) Tout parcours est, d'après l'énoncé, assimilable à une 7-liste de l'ensemble $\{R\;,\ V\;,\ O\}.$ Le nombre de tels parcours est donc 37 = 2187.

 

2) a) Les parcours tels que "Tous les feux sauf le premier sont au rouge" sont les 7-listes de $\{R\;,\ V\;,\ O\}$ du type $(X\;,\ R\;,\ R\;,\ R\;,\ R\;,\ R\;,\ R)$, où $X$ est l'une des couleurs $V$ ou $O.$ Le nombre de telles listes est donc, d'après le Principe Multiplicatif : $2\times 1^{6}=2.$

 

b) Les parcours tels que "Le premier des feux est au vert" sont les 7-listes de $\{R\;,\ V\;,\ O\}$ pour lesquels il y a 1 choix possible pour la première composante (c'est nécessairement un $V)$ et 3 choix possibles pour chacune des 6 autres composantes (cela peut être n'importe laquelle des 3 couleurs $R\;,\ V$ ou $O)$, d'où $1\times 3^{6}=729$ parcours de ce genre.

 

c) Les parcours tels que "Tous les feux sauf un sont au rouge" sont au nombre de : 7 (choix de l'emplacement du feu qui n'est pas rouge)$\times$ 2 (choix de la couleur de ce feu)$\times 1^{6}$=14 parcours de ce genre.

 

d) Les parcours où l'automobiliste s'arrête $k$ fois $(k\geq 5)$ sont au nombre de : $C_{7}^{k}$ (choix de l'emplacement des feux qui ne sont pas verts)$\times 2^{k}$(choix des couleurs de ces feux)$\times 1^{7-k}.$

Les parcours où l'automobiliste s'arrête au moins 5 fois sont donc au nombre de : $$C_{7}^{5}\times 2^{5}\times 1^{2}+C_{7}^{6}\times 2^{6}\times 1^{6}+C_{7}^{7}\times 2^{7}=1248$$

1) Les nombres complexes $(1+\mathrm{i})$ et $(1-\mathrm{i})$ sont conjugués, donc il en est de même de $(1+\mathrm{i})^{2015}$ et $(1-\mathrm{i})^{2015}$ d'après la propriété : $\bar{z^{n}}=\bar{z}^{n}$ et par conséquent la somme $Z=(1+\mathrm{i})^{2015}+(1-\mathrm{i})^{2015}$ est un réel d'après la propriété : $z+\bar{z}\in\mathbb{R}.$

 

2) On a sous forme exponentielle : $1+\mathrm{i}=\mathrm{e}^{\mathrm{i}\frac{\pi}{4}}$ et $1-\mathrm{i}=\mathrm{e}^{-\mathrm{i}\frac{\pi}{4}}$, d'où d'après la formule de Moivre : 

$\begin{array}{rcl} (1+\mathrm{i})^{2015}&=&\left(\mathrm{e}^{\mathrm{i}\frac{\pi}{4}}\right)^{2015}\\&=&\mathrm{e}^{\mathrm{i}\frac{2015\pi}{4}}\\&=&\mathrm{e}^{\mathrm{i}\frac{(2016-1)\pi}{4}}\\&=& \mathrm{e}^{\mathrm{i}\left(504\pi-\frac{\pi}{4}\right)} \\ &=& \mathrm{e}^{\mathrm{i}504\pi}\times\mathrm{e}^{-\mathrm{i}\frac{\pi}{4}} \\ &=&\mathrm{e}^{-\mathrm{i}\frac{\pi}{4}}\end{array}$
 

car 504 est pair et l'on a $\mathrm{e}^{\mathrm{i}2k\pi}=1\;,\ \forall\;k\in\mathbb{Z}.$

 

Il en résulte aussitôt, d'après 1), que : $(1-\mathrm{i})^{2015}=\mathrm{e}^{\mathrm{i}\frac{\pi}{4}}.$

 

On en déduit alors que :  $Z=\mathrm{e}^{-\mathrm{i}\frac{\pi}{4}}+\mathrm{e}^{\mathrm{i}\frac{\pi}{4}}=2\Re\left(\mathrm{e}^{\mathrm{i}\frac{\pi}{4}}\right)=2\times\dfrac{\sqrt{2}}{2}=\sqrt{2}.$