Corrigé Bac Maths S2-S2A-S4-S5 1er groupe - 2021

 

 

2) $p(A)=\dfrac{1}{2}$ ; 

 

$$\begin{eqnarray} p(\overline{A}&=&1-p(A)\nonumber\\\\&=&1-\dfrac{1}{6}\nonumber\\\\&=&\dfrac{5}{6} \end{eqnarray}$$

 

3) Soit $\Omega$ l'univers

 

$B\subset\Omega\Rightarrow\;b=\cap\Omega$ ; 

 

$A\cup\overline{A}=\Omega$ ; 

 

$B=B\cap\left(A\cup\overline{A}\right)$ 

 

$\Rightarrow\;B=(B\cap\;A)\cup\left(B\cap\overline{A}\right)$ ;

 

$$\begin{eqnarray} (B\cap\;A)\cap\left(B\cap\overline{A}\right)&=&B\cap\;A\cap\overline{A}\nonumber\\\\&=&B\cap\phi\nonumber\\\\&=&\phi \end{eqnarray}$$

 

$$\begin{eqnarray} p(B)&=&p(B\cap\;A)+p\left(B\cap\;\overline{A}\right)\nonumber\\\\&=&p(A)p(B/A)+p\left(\overline{A}\right)p\left(B/\overline{A}\right) \end{eqnarray}$$

 

$$\begin{eqnarray} p(B)&=&\dfrac{1}{6}\times\dfrac{3}{7}+\dfrac{5}{6}\times\dfrac{2}{5}\nonumber\\\\&=&\dfrac{1}{14}+\dfrac{1}{3}\nonumber\\\\&=&\dfrac{17}{42} \end{eqnarray}$$

 

$$\begin{eqnarray} 4)\quad p(A/B)&=&\dfrac{p(A\cap\;B)}{p(B)}\nonumber\\\\&=&\dfrac{p(A)p(B/A)}{p(B)}\nonumber\\\\&=&\dfrac{\dfrac{1}{6}\times\dfrac{3}{7}}{\dfrac{17}{42}}\nonumber\\\\p(A/B)&=&\dfrac{\dfrac{3}{22}}{\dfrac{17}{42}}\nonumber\\\\&=&\dfrac{3}{17} \end{eqnarray}$$

 

5) a) On a une suite d'épreuves de Bernoulli. L'expérience est répétée $5$ fois et n'a que $2$ issues :

 

le succès ou l'échec.

 

Le succès $(S)$ : « obtenir une boule blanche »

 

L'échec $(E)$ : « obtenir une boule non blanche »

 

$p(S)=p=p(B)=p\dfrac{17}{42}$ ; 

 

$p(E)=1-p$

 

Soit $\mathcal{U}$ l'ensemble des valeurs possibles de $X.$

 

$\mathcal{U}=\{0\;,\ 1\;,\ 2\;,\ 3\;,\ 4\;,\ 5\}$

 

$\begin{array}{lll} \forall\;k\in\mathcal{U}\;,\ p(X=k)&=&C_{5}^{k}p^{k}(1-p)^{5-k}\\\\&=&C_{5}^{k}\left(\dfrac{17}{42}\right)^{k}\left(1-\dfrac{17}{42}\right)^{5-k}\\\\p(X=k)&=&C_{5}^{k}\left(\dfrac{17}{42}\right)^{k}\left(\dfrac{25}{42}\right)^{5-k}\ ;\ k\in\mathcal{U} \end{array}$

 

$\begin{array}{lll} \text{b)}\quad E(X)&=&n\;p\\\\&=&5\times\dfrac{17}{42}\\\\&=&\dfrac{85}{42}\ ;\end{array}$

 

$\begin{array}{lll} V(X)&=&n\;p(1-p)\\\\&=&5\times\dfrac{17}{42}\times\dfrac{25}{42}\\\\&=&\dfrac{2125}{1764} \end{array}$

 

6) Soit $C$ l'événement "obtenir au moins une boule blanche".

 

Alors $\overline{C}$ est l'événement "obtenir $n$ boules non blanche"

 

$$\begin{eqnarray} p(\overline{C})&=&(1-p)^{n}\nonumber\\\\&=&\left(\dfrac{25}{42}\right)^{n} \end{eqnarray}$$

 

$$\begin{eqnarray} p(C)&=&1-p(\overline{C})\nonumber\\\\&=&1-\left(\dfrac{25}{42}\right)^{n} \end{eqnarray}$$

 

$$\begin{eqnarray} p(C)>0.99&\Leftrightarrow &1-\left(\dfrac{25}{42}\right)^{n}>0.99\nonumber\\\\&\Leftrightarrow &1-0.99>\left(\dfrac{25}{42}\right)^{n}\nonumber\\\\&\Leftrightarrow &0.01>\left(\dfrac{25}{42}\right)^{n}\nonumber\\\\&\Leftrightarrow &\ln(0.01)>\ln\left(\dfrac{25}{42}\right)^{n}\nonumber\\\\&\Leftrightarrow &\ln(0.01)>n\ln\left(\dfrac{25}{42}\right)\nonumber\\\\ &\Leftrightarrow &\dfrac{\ln(0.01)}{\ln\left(\dfrac{25}{42}\right)}<n\nonumber\\\\ &\Leftrightarrow &n>8.876\ldots \end{eqnarray}$$

 

$\text{or }n\in\mathbb{N}\;,\ \text{donc }n\geq 9.$

 

La valeur minimale de $n$ est $n_{0}=9.$

$$\begin{eqnarray} 1)\quad\text{a)}\quad a(1+\mathrm{i})&=&1+3\mathrm{i}\nonumber\\\\\Rightarrow\;a &=&\dfrac{1+3\mathrm{i}}{1+\mathrm{i}}\nonumber\\\\ &=&\dfrac{(1+3\mathrm{i})(1-\mathrm{i})}{(1+\mathrm{i})(1-\mathrm{i})}\nonumber\\\\ &=&\dfrac{4+2\mathrm{i}}{2}\nonumber\\\\ &=&2+\mathrm{i}\nonumber\\\\\;\mathrm{i}a^{2}&=&\mathrm{i}(2+\mathrm{i})^{2}\nonumber\\\\ &=&\mathrm{i}(3+4\mathrm{i})\nonumber\\\\ &=&-4+3\mathrm{i} \end{eqnarray}$$

 

$$\begin{eqnarray} \text{b)}\quad a^{2}-(1+3\mathrm{i})a-4+3\mathrm{i}&=&(2+\mathrm{i})^{2}-(1+3\mathrm{i})(2+\mathrm{i})-4+3\mathrm{i}\nonumber\\\\ &=&3+4\mathrm{i}+1-7\mathrm{i}-4+3\mathrm{i}\nonumber\\\\ &=&0 \end{eqnarray}$$

 

donc $a$ est solution de l'équation.

 

$$\begin{eqnarray} (\mathrm{i}a)^{2}-(1+3\mathrm{i})(\mathrm{i}a)-4+3\mathrm{i}&=&-a^{2}-\mathrm{i})^{2}-(1+3\mathrm{i})(2+\mathrm{i})-4+3\mathrm{i}\nonumber\\\\ &=&-3-4\mathrm{i}+\mathrm{i} (1-7\mathrm{i})-4+3\mathrm{i}\nonumber\\\\&=&-3-4\mathrm{i}+\mathrm{i}+7-4+3\mathrm{i}\nonumber\\\\ &=&0 \end{eqnarray}$$

 

donc $\mathrm{i}a$ est une solution de l'équation.

 

2) a)

 

 

 

 

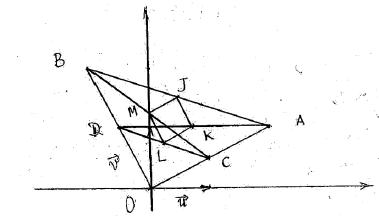
$$\begin{eqnarray} 3)\quad\text{a)}\quad OCD\text{ est isocèle et }\left(\widehat{\overrightarrow{OC}\;,\ \overrightarrow{OD}}\right) &=&\dfrac{\pi}{2}\nonumber\\\\\Rightarrow\;OC &=&OD\nonumber\\\\\text{et }\left(\widehat{\overrightarrow{OC}\;,\ \overrightarrow{OD}}\right) &=&\dfrac{\pi}{2}\nonumber\\\\\Rightarrow|c|&=&|d|\nonumber\\\\\text{et arg}\left(\dfrac{d}{c}\right)&=&\dfrac{\pi}{2}\nonumber\\\\\Rightarrow\dfrac{|d|}{||c}&=&1\nonumber\\\\\text{et arg}\left(\dfrac{d}{c}\right)&=&\dfrac{\pi}{2}\nonumber\\\\\Rightarrow\left|\dfrac{d}{c}\right|&=&1\nonumber\\\\\text{et arg}\left(\dfrac{d}{c}\right)&=&\dfrac{\pi}{2}\nonumber\\\\\Rightarrow\dfrac{d}{c}&=&\mathrm{e}^{\mathrm{i}\dfrac{\pi}{2}}\nonumber\\\\\Rightarrow\dfrac{d}{c}&=&\mathrm{i}\nonumber\\\\\;d&=&\mathrm{i}c\nonumber\\\\\Rightarrow\;d&=&\mathrm{i}\left(1+\dfrac{1}{2}\mathrm{i}\right)\nonumber\\\\\Rightarrow\;d&=&-\dfrac{1}{2}+\mathrm{i} \end{eqnarray}$$

 

$$\begin{eqnarray} \text{b)}\quad j\text{ milieu de }[AB]\Rightarrow\;z_{J}&=&\dfrac{1}{2}(a+b)\nonumber\\\\ &=&\dfrac{1}{2}(2+\mathrm{i}-1+2\mathrm{i})\nonumber\\\\ &=&\dfrac{1}{2}(1+3\mathrm{i})\nonumber\\\\ &=&\dfrac{1}{2}+\dfrac{3}{2}\mathrm{i} \end{eqnarray}$$

 

$$\begin{eqnarray} K\text{ milieu de }[DA]\Rightarrow\;z_{K}&=&\dfrac{1}{2}(a+d)\nonumber\\\\ &=&\dfrac{1}{2}\left(2+\mathrm{i}-\dfrac{1}{2}+\mathrm{i}\right)\nonumber\\\\ &=&\dfrac{1}{2}\left(\dfrac{3}{2}+2\mathrm{i}\right)\nonumber\\\\ &=&\dfrac{3}{4}+\mathrm{i} \end{eqnarray}$$

 

$$\begin{eqnarray} L\text{ milieu de }[CD]\Rightarrow\;z_{L}&=&\dfrac{1}{2}(c+d)\nonumber\\\\ &=&\dfrac{1}{2}\left(1+\dfrac{1}{2}\mathrm{i}-\dfrac{1}{2}+\mathrm{i}\right)\nonumber\\\\ &=&\dfrac{1}{2}\left(\dfrac{1}{2}+\dfrac{3}{2}\mathrm{i}\right)\nonumber\\\\ &=&\dfrac{1}{4}+\dfrac{3}{4}\mathrm{i} \end{eqnarray}$$

 

$$\begin{eqnarray} M\text{ milieu de }[BC]\Rightarrow\;z_{M}&=&\dfrac{1}{2}(b+c)\nonumber\\\\ &=&\dfrac{1}{2}\left(-1+2\mathrm{i}+1+\dfrac{1}{2}\mathrm{i}\right)\nonumber\\\\ &=&\dfrac{1}{2}\left(\dfrac{5}{2}\mathrm{i}\right)\nonumber\\\\ &=&\dfrac{5}{4}\mathrm{i} \end{eqnarray}$$

 

$$\left.\begin{array}{lllll} z_{J}-z_{K}&=&\dfrac{1}{2}+\dfrac{3}{2}\mathrm{i}-\dfrac{3}{4}-\mathrm{i}&=&-\dfrac{1}{4}+\dfrac{1}{2}\mathrm{i}\\\\ z_{M}-z_{L}&=&\dfrac{5}{4}\mathrm{i}-\dfrac{1}{4}-\dfrac{3}{4}\mathrm{i}&=&-\dfrac{1}{4}+\dfrac{1}{2}\mathrm{i} \end{array}\right\rbrace$$

 

$$\begin{eqnarray} \Rightarrow\;z_{J}-z_{K}&=&z_{M}-z_{L}\nonumber\\\\\Rightarrow\overrightarrow{KJ}&=&\overrightarrow{LM}\nonumber\\\\\;KJ&=&\left|z_{J}-z_{K}\right|\nonumber\\\\ &=&\sqrt{\left(-\dfrac{1}{4}\right)^{2}+\left(\dfrac{1}{2}\right)^{2}}\nonumber\\\\ &=&\sqrt{\dfrac{1}{16}+\dfrac{1}{4}}\nonumber\\\\ &=&\sqrt{\dfrac{5}{16}}\nonumber\\\\ KJ&=&\dfrac{\sqrt{5}}{4} \end{eqnarray}$$

 

$$\begin{eqnarray} KL&=&\left|z_{L}-z_{K}\right|\nonumber\\\\ &=&\left|\dfrac{1}{4}+\dfrac{3}{4}\mathrm{i}-\dfrac{3}{4}-\mathrm{i}\right|\nonumber\\\\ &=&\left|-\dfrac{1}{2}-\dfrac{1}{4}\mathrm{i}\right|\nonumber\\\\ &=&\sqrt{\left(-\dfrac{1}{2}\right)^{2}+\left(-\dfrac{1}{4}\right)^{2}}\nonumber\\\\ KL&=&\sqrt{\dfrac{1}{4}+\dfrac{1}{16}}\nonumber\\\\ &=&\dfrac{\sqrt{5}}{4} \end{eqnarray}$$

 

$KJ=\dfrac{\sqrt{5}}{4}\quad\text{et}\quad KL=\dfrac{\sqrt{5}}{4}\ ;\ \text{donc }KJ=KL$