BFEM Mathématiques 2010
Exercice 1 (5 points)
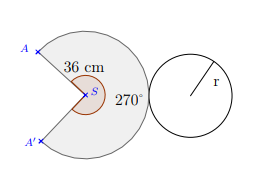
Le schéma ci-contre représente le patron d'un cône de révolution de sommet S, de rayon de base r.
La génératrice [SA] a pour longueur 36cm.
1) Justifie que la circonférence de sa base mesure 54πcm.(1pt)
2) Montre que son rayon de base r vaut 27cm.(1pt)
3) Justifie que la hauteur de ce cône est égale à 9√7cm(1pt)
4) Calcule l'aire de la surface totale de ce cône.(1.5pt)
On prendra π=3.14
Exercice 2 (5 points)
ABC est un triangle rectangle en A tel que :
AB+AC+BC=72cm et 4AB=3AC
1) Sans calculer les longueurs des cotés du triangle ABC, montre que :
a) 7AB+3BC=216cm;(1.5pt)
b) 3BC−5AB=0.(1.5pt)
2) En utilisant les résultats de la question 1), calcule AB et BC ; déduis-en AC.(2pt)
Exercice 3 (6 points)
Un commerçant fixe le prix de vente de chacun de ses articles en prévoyant un bénéfice de 25 pour cent.
Soit x le prix d'achat d'un article et p son prix de vente.
1) Justifie que :
p=54x(1pt)
2) Calcule le prix de vente d'un article acheté à 400 F.(1pt)
3) Calcule le prix d'achat d'un article vendu à 1250 F.(1pt)
4) Représente graphiquement dans un repère orthonormal (O, →i, →j), où 1cm représente 100 F, l'application qui à x associe p.(2pt)
5) Détermine graphiquement le prix d'achat d'un article vendu à 750 F.(1pt)
Exercice 4 (4 points)
On donne l'expression
A(x)=(2x+1)(5x+1)−(4x+2)(x−2)
A(x)=(2x+1)(5x+1)−(4x+2)(x−2)
1) Développe et réduis A(x).(1pt)
2) Factorise A(x).(1pt)
3) Résous dans R l'inéquation :
Commentaires
seck (non vérifié)
dim, 06/06/2021 - 20:57
Permalien
Exercice 1
Alimatou ndao (non vérifié)
mer, 07/13/2022 - 14:15
Permalien
D après notre professeur de
Ajouter un commentaire