BFEM Mathématiques 2019

 

Exercice 1 (5 points)

1) Dis comment obtenir la valeur de la médiane d'une série statistique ordonnée à caractère quantitatif discret et d'effectif total $N.$
 
2) Le tableau ci-dessous donne la répartition des salaires mensuels en $\text{F CFA}$ et leurs proportions pour le personnel d'une entreprise.
$$\begin{array}{|l|c|c|} \hline \text{Fonctions}&\text{Fréquences en pourcentage}&\text{Salaires}\\ \hline \text{Cadres supérieurs}&5&450\, 000\\ \hline \text{Agents de production}&45&350\,000\\ \hline \text{Personnels administratifs}&15&200\,000\\ \hline \text{Chauffeurs}&5&150\,000\\ \hline \text{Agents de sécurité}&10&100\,000\\ \hline \text{Agents commerciaux}&20&175\,000\\ \hline \end{array}$$
 
a) Indique le caractère étudié et sa nature.
 
b) Calcul le salaire moyen mensuel dans cette entreprise.
 
3) Calcul le salaire médian de cette entreprise sachant qu'il y a exactement $2$ cadres qui y travaillent.
 
4) Construis le diagramme des fréquences cumulées croissantes de cette série.
 

Exercice 2 (05 points)

Soit $ABCD$ un rectangle tel que $AB=12\;cm\ $ et $\ BC=x\;cm\ $ avec $\ 0<x<12.$
 
1) Calcule le périmètre $P$ du rectangle en fonction de $x.$
 
2) Dans quel intervalle peut-on choisir $x$ pour que $P$ soit supérieur à $33\;cm\ ?$
 
3) Calcul l'aire $\mathcal{A}$ de la surface de ce rectangle en fonction de $x.$
 
4) Dans quel intervalle peut-on choisir $x$ pour que $\mathcal{A}$ soit inférieur à $81\;cm^{2}\ ?$
 
5) On donne $x=9\ $ et $\ A'B'C'D'$ un carré dont l'aire est égale à celle du rectangle $ABCD.$
 
a) Calcule le côté du carré.
 
b) Compare le périmètre $P$ du rectangle et celui $P'$ du carré.

Exercice 3 (5 points)

Le plan est muni d'un repère orthonormal $(O\;;\ \vec{i}\;;\ \vec{j}).$
 
1) Place les points $A(-3\;;\ 3)\;,\ B(5\;;\ -1)\ $ et $\ C(5\;;\ 9).$
 
2) Trouve une équation de la droite $(\Delta)$ hauteur du triangle $ABC$ passant par le point $C.$
 
Soit le point $K$ milieu de $[BA].$
 
a) Vérifie que $K$ appartient à $(\Delta).$
 
b) Déduis-en la nature du triangle $ABC$ et celle du triangle $AKC.$
 
3) Soit $(\mathcal{C})$ le cercle circonscrit au triangle $AKC.$
 
a) Détermine les cordonnées de son centre $L$ et calcule son rayon $R.$
 
b) Montre que $M(6\;;\ 6)$ appartient au cercle $(\mathcal{C})$
 
c) Justifie que $\widehat{AMK}\ $ et $\ \widehat{ACK}$ ont la même mesure
 
d) Montre que $\widehat{CAK}\ $ et $\ \widehat{AMK}$ sont complémentaires
 

Exercice 4 (5 points)

1) Le schéma ci-dessous représente le patron de la partie latérale d'un cône de révolution.
 
 
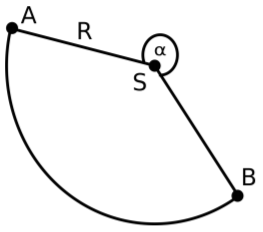
Justifie que le rayon $r$ de la base du cône vaut $r=R\times\left(1-\dfrac{\alpha}{360^{\circ}}\right).$
 
2) Démontre que la hauteur $h$ du cône vaut : $h=R\times\sqrt{1-\left(1-\dfrac{\alpha}{360}\right)^{2}}.$
 
3) Exprime l'aire du cône en fonction de $R\ $ et $\ \alpha.$
 
4) On pose $\alpha=270^{\circ}\;,\ R=50\;cm\ $ et $\ \pi\backsimeq 3.14.$
 

 

Commentaires

Faye Abdoulaye (non vérifié)

lun, 03/02/2020 - 22:16

Les gosses ne comprennent plus le français . C'est la raison pour laquelle beaucoup ont mordu leur stylo.

Anonyme (non vérifié)

lun, 05/25/2020 - 16:03

Merci Intéressant

Anonyme (non vérifié)

dim, 08/02/2020 - 20:20

C'est très intéressant pour les élèves

Mouhamed (non vérifié)

dim, 09/13/2020 - 11:33

merci beaucoup

Seynabou(non vé... (non vérifié)

mer, 12/09/2020 - 22:49

Merci ses gentil

Seynabou(non vé... (non vérifié)

mer, 12/09/2020 - 22:49

Merci ses gentil

Abibatou diaw (non vérifié)

lun, 07/12/2021 - 11:47

Je fais la classe de troisième et je veux traiter ces exercices de maths .MERCI

Abibatou diaw (non vérifié)

lun, 07/12/2021 - 11:50

Je fais la classe de troisième et je veux traiter ces exercices de maths. MERCI

Anonyme (non vérifié)

jeu, 07/15/2021 - 13:51

Merci c'est intéressant

Anonyme (non vérifié)

dim, 11/14/2021 - 11:59

Montrer les tabeaux

Laurent Dupont (non vérifié)

jeu, 06/09/2022 - 20:53

tres pratique pour les revisions en vue du bfem et il faut neanmoins reconnaitre que je ne sais rien lol mais comme dirait Socrates a ses disciples non seulement vous ne savez pas mais vous croyez savoir car il faut souligner que la premiere etape du savoir scientifique est de reconnaitre que l'on ne sait pas Laurent DUPONT Paris

Ajouter un commentaire