Pour chacune des questions dans le tableau ci-dessous, trois réponses $A\;,\ B\ $ et $\ C$ sont proposées dont une seule est correcte.

 

Pour répondre, tu porteras sur ta copie, le numéro de la question suivi de la lettre correspondant à la réponse choisie.

 

Chaque réponse correcte est notée $0.75$ points.

 

Une réponse fausse ou une absence de réponse est notée $0$ point.

$$\begin{array}{|c|l|c|c|c|} \hline N^{\circ}&\qquad\quad\text{Questions}&\text{Réponse A}&\text{Réponse B}&\text{Réponse C}\\\hline&\text{On considère deux angles }\widehat{A}\text{ et }\widehat{B}\text{ tels que :}&&&\\1&\widehat{A}=90-\widehat{B}&\cos\widehat{A}=\cos\widehat{B}&\cos\widehat{A}=\sin\widehat{B}&\sin\widehat{A}=\sin\widehat{B}\\&\text{Quelle relation a-t-on ?}&&&\\\hline&\text{Soit }MNP\text{ un triangle rectangle en }N\text{ tel que :}&&&\\2&MN=6\;cm\text{ et }\widehat{MPN}=30^{\circ}&3\;cm&12\;cm&6\;cm\\&\text{Quelle est la mesure de la longueur de }[MP]\ ?&&& \\\hline &\text{On donne une droite }(D)\text{ d'équation :}&&&\\3&3y=6x+2\text{ dans un repère orthonormal.}&\dfrac{3}{2}&\dfrac{2}{3}&2\\&\text{Quel est le coefficient directeur de la droite }(D)\ ?&&&\\\hline&\text{Soient }\vec{u}\begin{pmatrix} -3\\1\end{pmatrix}\text{ et }\vec{v}\begin{pmatrix} 2\\y\end{pmatrix}\text{ deux vecteurs du plan.}&&&\\4&\text{Pour quelle valeur de }y\text{ les vecteurs }\vec{u}\text{ et }\vec{v}&y=-\dfrac{2}{3}&y=-\dfrac{3}{2}&y=-6\\&\text{sont-ils colinéaires ?}&&&\\\hline&\text{Dans un repère orthonormal, pour quelles valeurs de}&&&\\5&n\text{, les vecteurs }\vec{u}\begin{pmatrix} n\\1\end{pmatrix}\text{ et }\vec{v}\begin{pmatrix} n\\-4\end{pmatrix}&n=1\text{ ou }n=4&n=4\text{ ou }n=-4&n=2\text{ ou }n=-2\\&\text{sont-ils orthogonaux ?}&&&\\\hline&\text{Quelle est l'aire latérale }A_{l}\text{ d'un cône de révolution}&&&\\6&\text{de génératrice }g,\text{ de hauteur }h&\pi gh&\pi r^{2}g&rg\pi\\&\text{et de rayon de base }r\ ?&&&\\ \hline \end{array}$$

1) Résous dans $\mathbb{R}$ l'équation $6x^{2}-4x+5=-x^{2}-4x+9.$

 

2) On considère l'inéquation $2(x-3)(2x+3)\leq 0.$

 

a) Détermine le signe de $12-18\sqrt{3}$ puis déduis-en que le réel $3-\sqrt{3}$ est une solution de cette inéquation.

 

b) Résous dans $\mathbb{R}$ l'inéquation $2(x-3)(2x+3)\leq 0.$

 

3) Montre que $4\sqrt{3}-2\sqrt{75}+4\sqrt{12}-\sqrt{27}+\sqrt{9}=3-\sqrt{3}.$

 

4) Donne un encadrement de $3-\sqrt{3}$ à $10^{-2}$ près, sachant que $1.732<\sqrt{3}<1.733.$

A la suite des brillants résultats obtenus par ses enfants, un père de famille décide d'organiser une fête en leur honneur.

 

Connaissant les vertus de la viande, il décide d'acheter des pintades et des pigeons.

 

Sur le marché, un pigeon coûte $2\,000\;F$ et une pintade coûte $5\,000\;F.$

 

On désigne par $x$ le nombre de pigeons et $y$ celui de pintades.

 

1) Le père veut acheter $10$ volailles avec une somme de $32\,000\;F.$

 

a) Traduis cette situation par un système d'équations.

 

b) Calcule $x\ $ et $\ y.$

 

2) Voyant que le nombre d'invités peut augmenter, le père décide d'acheter plus de $12$ volailles mais ne compte pas dépenser plus de $36\,000\;F.$

 

a) Traduis cette situation par un système d'inéquations.

 

b) Résous graphiquement ce système d'inéquations.

 

En se servant du graphique, détermine :

 

i) les nombres possibles de pintades qu'il peut avoir s'il décide d'acheter $13$ pigeons ?

 

ii) toutes les possibilités d'achat de ces volailles.

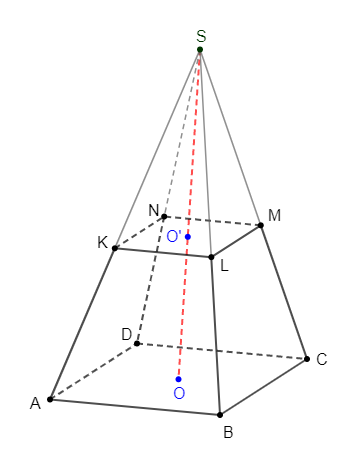
On considère une pyramide régulière $SABCD$, de sommet $S$ et de base $ABCD.$

 

On sectionne cette pyramide par un plan parallèle à sa base passant par $O'$ comme indiqué sur la figure ci-dessous.

 

La pyramide $SABCD$ a une hauteur $SO=6\,dm$ et un volume $V_{1}=32\,dm^{3}.$

 

Le carré $KLMN$ a pour coté $3\,dm.$

1) Justifie que l'aire de la base $ABCD$ est égale à $16\,dm^{2}.$

 

2) Montre que le coefficient de réduction de la pyramide $SABCD$ en la pyramide $SKLMN$ est $\dfrac{3}{4}.$

 

3) Calcule le volume $V_{2}$ de la pyramide $SKLMN.$

 

4) Un entrepreneur veut fabriquer des bornes en béton identiques ayant la même forme et les mêmes dimensions que le solide $ABCDKLMN.$

 

Combien pourrait-il en faire s'il dispose d'une quantité de $1.85\,m^{3}$ de béton ?

$\begin{array}{c}\blacktriangleright\ \boxed{\text{Correction BFEM 2022}}\end{array}$