Corrigé BFEM mathématique 1er groupe - 2024

 

Pour chacune des questions dans le tableau ci-dessous, trois réponses $A$, $B$, et $C$ sont proposées dons une seule est correcte.

 

Pour répondre, tu pourras sur ta copie, le numéro de la question suivie de la lettre correspondant à la réponse choisie.

 

Chaque réponse correcte est notée $0.75$ 

 

$\begin{array}{|c|c|c|c|} \hline N^{\circ}&\text{Questions}&\text{Réponses }A&\text{Réponses }B&\text{Réponses }C\\ 1&\text{Quelle est la valeur du réel }M=\sqrt{\dfrac{2-\sqrt{3}}{2+\sqrt{3}}}?&&2-\sqrt{3}&\\ \hline 2&\text{Quel est l'ensemble des solutions }&&&\\ &\text{dans }\mathbb{R}\text{ de l'inéquation }(-4x+8)(3x-5)\geq 0?&&&\left(\dfrac{5}{3}\;,2\right)\\ \hline &\text{Pour quelles valeurs de }m\text{ le couple }\left(-2\;,m^{2}\right)&m=-2&&\\ 3&\text{est solution de l'équation }-x-y+2=0?&\text{ ou }&&\\ &&m=2&&\\ \hline &\text{Les triangles }MOI\text{ et }MAB\text{ sont tels que les }&&&\\ &\text{points }M\;,O\;,A\text{ d'une part et }M\;,I\;,B\text{ d'autre part }&&&\text{Elles sont}\\ 4&\text{soient alignés dans cet ordre. }&&&\text{parallèles}\\ &\text{Si }\dfrac{MA}{MO}=\dfrac{MB}{MI}\;,\text{ quelle est la }&&&\\ &\text{position relative des droites }&&&\\ &(OI)\text{ et }(AB)?&&&\\ \hline &MNP\text{est un triangle rectangle en }&&&\\ 5&M\text{tel que }\sin\left(\overbrace{MPN}\right)=\dfrac{1}{2}&&&60^{\circ}\\ &\text{Quelle est la mesure de l'angle }\overbrace{MNP}?&&&\\ \hline 6&\text{Soit }\alpha\text{ un réel }&&&\\ &\text{Dans le plan est muni d'un repère }&&1&\\ &\text{orthonormé, por quelle valeur de }&&&\\ &\alpha\text{, les vecteurs }\overrightarrow{AB}(\alpha\;,4)&&&\\ &\text{et }\overrightarrow{CD}(-8\;,2)\text{sont-ils orthogonaux ?}&&&\\ \hline 7&\text{Quelle est l'expression de l'application }&&&-\dfrac{1}{3}x+5\\ &\text{affine }h\text{telle que }h(-3)=6?&&&\\ \hline &\text{Quel est le couple de solution du système }&&&\\ 8&\text{d'équations }\left\lbrace\begin{array}{rcl} 2x-y-1&=&0\\ ? 3x+5y&=&21 \end{array}\right.&(2.3)&&\\ \hline \end{array}$ 

 

 

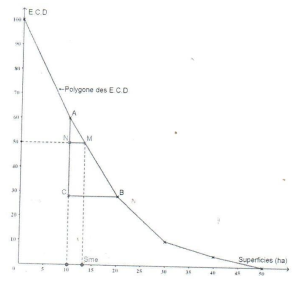
Les données consignées dans le tableau ci-dessous sont celles de superficies en hectares $(ha)$ attribuées à des habitants d'une régions par un Conseil Municipal.

 

$\begin{array}{|c|c|c|c|c|c|} \hline \text{Superficies }(ha)&]0\;,10]&]10\;,20]&]20\;,30]&]30\;,40]&]40\;,50]\\ \hline \text{Effectifs cumulés }&&&&&\\ \text{décroissants }100&60&28&10&4\\ \hline \end{array}$

 

Pour que l'affectation des terres soit valable, elle doit être approuvée par le Sous-préfet, le préfet, ou Gouverneur selon la Superficie $S$ attribuée.

 

 sous-préfet approuve une superficie $S$ telle que $S\leq 10\;,ha.$

 

$\blacktriangleright$ Le préfet approuve une superficie $S$ telle que $10\;,ha\leq 50\;,ha.$

 

$\blacktriangleright$ Le gouverneur approuve une superficie $S$ telle que $S>50\;,ha.$

 

Le Conseil Municipal a besoin de la superficie moyenne $S_{m}.$ et de la superficie médiane $S_{me}.$

 

I. Détermine l'intervalle contenant les superficies attribuées au plus grand nombre d'habitants de la région.

 

 

$\begin{array}{|c|c|c|c|c|c|c|} \hline \text{Superficies }(ha)&]0\;,10]&]10\;,20]&]20\;,30]&]30\;,40]&]40\;,50]&\text{Total}\\ \hline \text{Effectifs cumulés }&100&60&28&10&4&\\ \text{décroisantq }&&&&&&\\ \hline \text{affectifs }&40&32&18&6&4&100\\ \hline \end{array}$

 

L'intervalle contenant les superficies attribuées au plus grand nombres d'habitants de la région est $]0\;,10]$

 

NB : Tout candidat qui déterminerait cet intervalle par une autre méthode correcte obtiendrait le total de $1.5$ point

 

2. En s'appuyant sur les connaissances en statistique, aide ce Conseil Municipal à calculer $S_{m}$ et $S_{me}$

 

$\begin{array}{|c|c|c|c|c|c|c|} \hline \text{Superficies }(ha)&]0\ ;\ 10]&]10\ ;\ 20&]20\ ;\ 30]&]30\ ;\ 40]&]40\ ;\ 50]&\text{Total}\\ \hline \text{Effectifs cumulés décroissants }&100&60&28&10&4&\\ \hline \text{Effectifs }&40&32&18&6&4&100\\ \hline \text{Centre }&5&15&25&35&45&\\ \hline \text{Produits effectifs }\times\text{ centre }&200&480&450&210&180&1520\\ \hline \end{array}$

 

Détermination de la moyenne est : $S_{m}=\dfrac{1520}{100}$

$$S_{m}=15.20\;,ha$$

 

Détermination de la médiane

 

On considère les triangles $AMN$ et $ABC$ où les points $M$ et $N$ appartiennent respectivement aux segments $[AB]$ et $[AC]$ telle que $(MN)$ et $(BC)$ soient parallèles.

 

D'après la conséquence du théorème de Thalès, on a : $$\dfrac{AM}{AB}=\dfrac{AN}{AC}=\dfrac{MN}{BC}$$

 

$\dfrac{AN}{AC}=\dfrac{MN}{BC}\text{équivaut à}\dfrac{S_{me}-10}{20-10}=\dfrac{60-50}{60-28}$

 

$\dfrac{S_{me}-10}{10}=\dfrac{10}{32}\ ;\ S_{me}=\dfrac{100}{32}+10$

 

$S_{me}=13.125\;,ha$

 

3.a. Calcule le pourcentage de personnes dont l'attribution des superficies $S$ est approuvée par le Sous-préfet.

 

Le pourcentage de personnes dont l'attribution des superficies $S$ est approuvée par le Sous-préfet est : 

 

$\dfrac{40}{100}\times\;,\text{ soit }40\%$

 

b. Calcule le pourcentage de personnes dont l'attribution des superficies $S$ est approuvée par le Préfet.

 

Le pourcentage de personnes dont l'attribution des superficies $S$ est approuvée par le préfet est :

 

$\dfrac{(32+18+64)}{100}\times 100=\dfrac{60}{100}\times 100$ soit $60\%$

 

 

On considère le cercle de centre $O$ et de rayon $R=1.2\;,cm.$

 

Les segments $[FA]$ et $[CE]$ sont des diamètres de ce cercle et $\overbrace{OAC}=54^{\circ}$

 

 

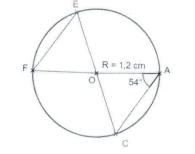
1. Calcule $\overbrace{FOC}$ et $\overbrace{FEC}$

 

$\blacktriangleright$ l'angle $\overbrace{FOC}$ est un angle au centre et $\overbrace{FAC}=\overbrace{OAC}=54^{\circ}$ est un angle inscrit.

 

Ils interceptent le même arc de centre $\overbrace{FC}$ donc $\overbrace{FOC}=2\times \overbrace{OAC}=2\times 54^{\circ}$ $$\overbrace{FOC}=108^{\circ}$$

 

$\blacktriangleright$ Les angles $\overbrace{FAC}\left(=\overbrace{OAC}=54^{\circ}\right)$ et $\overbrace{FEC}$ sont des angles inscrits qui interceptent le même arc de centre $\overbrace{FC}$ ; ils sont donc égaux. $$\overbrace{FEC}=54^{\circ}$$

 

2. Un patron d'un solide est constitué de sa base, un cercle de rayon $r$ et d'un secteur circulaire dont la longueur de l'arc de cercle est égale au périmètre de sa base

 

 

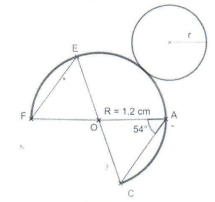
a. Comment appelle-t-on ce solide ?

 

Un tel solide est appelé cône revolution.

 

b. Calcule l'aire latérale $A_{L}$ de la surface $(S)$ de ce solide dont le patron est représenté par cette figure à gauche.

 

L'angle de développent du cône est $\alpha=360^{\circ}-FOC =\overbrace{360^{\circ}}-108^{\circ}=252^{\circ}$

 

Soit $r$ le rayon de la base.

 

On a :$\begin{array}{rcl} \dfrac{r}{R}&=&\dfrac{\alpha}{360^{\circ}}\\ \text{donc }r=R\times\dfrac{\alpha}{360^{\circ}}=1.2\,cm\times \dfrac{252^{\circ}}{360^{\circ}}\\ r=0.84\,cm \end{array}$

 

$A_{L}=\pi r R=\pi\times0.84\times 1.2$

 

$A_{L}=1.008\pi\,cm^{2}$

 

Autre méthode

 

$A_{L}=\dfrac{\pi\mathbb{R}^{2}\alpha}{360}=\dfrac{\pi\times (1.2)^{2}\times 252^{\circ}}{360^{\circ}}$

 

$A_{L}=1.008\pi\,cm^{2}$

 

NB : Tout candidat qui utiliserait rigoureusement une autre méthode correcte obtiendrait le total de $2$ points

 

3. Un groupement d'intérêt Économique $(GIE)$ qui s'active dans la production et la vente de jus locaux veut conserver sa production dans des boites représentées par le solide décrit dans la question précédente à l'échelle de $\dfrac{1}{10}$

 

Sachant que la production journalière en jus remplit un tonneau de forme cylindrique de rayon de base $0.5$ mètre et de hauteur $1.5$, détermine le nombre maximal de boites que le $GIE$ peut remplit journalière ment

 

$\blacktriangleright$ le volume du tonneau est : $V=\pi\times (0.5)^{2}\times 1.5=0.375\pi m^{3}$

 

 

$\blacktriangleright$ Calcul du volume d'une boite

 

On note $h$ la hauteur de sa base du cône représentant la boite.

 

On a : $h=\sqrt{R^{2}-r^{2}}=\sqrt{1.2^{2}-0.84^{2}}=\sqrt{0.7344}$

 

le volume d'une boite est donc : 

 

$\begin{array}{rcl} v&=&\dfrac{1}{3}\times\pi\times r^{2}\times h\\&=&\dfrac{1}{3}\times\pi\times 0.84^{2}\times\sqrt{0.7344}\times 10^{3}\,cm^{3} \end{array}$

 

$\blacktriangleright$ Soit $N$ le nombre maximal de bouteilles.

 

Le nombre $N$ est le plus petit entier inférieur $\dfrac{V}{v}$ $$\dfrac{V}{v}=\dfrac{0.375\pi\times 10^{6}}{\dfrac{1}{3}\times\pi 0.84^{2}\times\sqrt{0.7344}\times 10^{3}}$$

 

Le nombre maximal de bouteilles est $N=1860.$