Corrigé BFEM Maths 2018 2ième groupe

 

1) Les coordonnées du vecteur $\overrightarrow{RT}$ sont, d'après une formule du Cours $\begin{pmatrix} x_{T}&-x_{R}\\ y_{T}&-y_{R} \end{pmatrix}$ en désignant par $x_{M}$ et $y_{M}$ les coordonnées du point $M.$ 

 

En remplaçant par les valeurs données dans l'énoncé, on voit que $\overrightarrow{RT}$ a pour coordonnées $\begin{pmatrix} 1&-(-3)\\ -3&-5 \end{pmatrix}$, soit $\begin{pmatrix} 4\\ -8 \end{pmatrix}$.

 

La bonne réponse est donc la réponse 4)

 

2) La distance $RS$ est donnée par la formule : 

 

$RS=\sqrt{(x_{S}-x_{R})^{2}+(y_{S}-y_{R})^{2}}$, soit en remplaçant les coordonnées de $R$ et $S$ par leurs valeurs données dans l'énoncé, $\begin{array}{lcl}RS&=&\sqrt{(5-(-3))^{2}+(-1-5)^{2}}\\&=&\sqrt{64+36}\\&=&\sqrt{100}\\&=&10.\end{array}$

 

La bonne réponse est donc la réponse 3)

 

3) Le quadrilatère $RTSI$ est un parallélogramme si et seulement si on a l'égalité vectorielle $\overrightarrow{RT}=\overrightarrow{IS}.$ 

 

Or le couple de coordonnées du vecteur $\overrightarrow{RT}$ est $\begin{pmatrix} 4\\ -8 \end{pmatrix}$ (calcul déjà fait à la question 1) et celui du vecteur  $\overrightarrow{IS}$ est, en désignant par $x_{I}$ et $y_{I}$ les coordonnées du point $I$, $\begin{pmatrix} 5&-x_{I}\\ -1&-y_{I} \end{pmatrix}$, soit en remplaçant $x_{S}$ et $y_{S}$ par leurs valeurs respectives $5$ et $-1$, $\begin{pmatrix} 5&-x_{I}\\ -1&-y_{I} \end{pmatrix}.$

 

D'après la propriété d'égalité de deux vecteurs, on a : 

$\left\lbrace\begin{array}{lcl} 5-x_{I}&=&4\\ -1-y_{I}&=&-8 \end{array}\right.\ \Rightarrow$  $\left\lbrace\begin{array}{lcl} x_{I}&=&1\\ y_{I}&=&7 \end{array}\right.$

 

Le point $I$ a donc pour coordonnées $\begin{pmatrix} 1\\ 7 \end{pmatrix}$ et la bonne réponse est donc la réponse 3)

 

4) Il y a plusieurs méthodes pour déterminer une équation de la droite $(ST).$

 

Nous en donnerons deux.

 

$1^{er}$ méthode :

 

Un point $M(x\;;\ y)$ appartient à la droite $(ST)$ si et seulement si les vecteurs $\overrightarrow{ST}$ et $\overrightarrow{SM}$ sont colinéaires, ce qui se traduit, en désignant par $x_{\overrightarrow{u}}$ et $y_{\overrightarrow{u}}$ les coordonnées du vecteur $\overrightarrow{u}$, par :

$$x_{\overrightarrow{ST}}\cdot y_{\overrightarrow{SM}}-y_{\overrightarrow{ST}}\cdot x_{\overrightarrow{SM}}=0$$

 

Or le vecteur $\overrightarrow{ST}$ a pour coordonnées $\begin{pmatrix} x_{T}& x_{S}\\ y_{T}& y_{S} \end{pmatrix}$, soit $\begin{pmatrix} 1&-5\\ -3&-(-1) \end{pmatrix}$ ou encore $\begin{pmatrix} -4\\ -2 \end{pmatrix}$ et le vecteur $\overrightarrow{SM}$ a pour coordonnées $\begin{pmatrix} x&-x_{S}\\ y&-y_{S} \end{pmatrix}$, soit $\begin{pmatrix} x&-5\\ y&-(-1) \end{pmatrix}$ ou encore $\begin{pmatrix} x&-5\\ y&+1 \end{pmatrix}.$

 

La condition précédente s'écrit donc :

 

$-4(y+1)-(-2)(x-5)=0$, soit après simplification : 

 

$x-2y-7=0$, ce qui s'écrit également $2y=x-7$ ou $y=\dfrac{1}{2}x-\dfrac{7}{2}.$

 

$2^{ième}$ méthode :

 

Rappelons tout d'abord que si $\overrightarrow{u}$ $\begin{pmatrix} a\\ b \end{pmatrix}$ est un vecteur directeur de la droite $(AB)$, une équation de cette droite est de la forme $bx-ay+k=0$

 

Le vecteur $\overrightarrow{ST}$ $\begin{pmatrix} -4\\ -2 \end{pmatrix}$ (voir la méthode précédente) est un vecteur directeur de la droite $(ST).$ 

 

Ce vecteur, n'étant pas colinéaire à $\vec{j}$, une équation réduite de la droite $(ST)$ est de la forme :

 

$-2x+4y+k=0.$ 

 

Le point $S$ étant un point de cette droite, ses coordonnées doivent vérifier cette équation, d'où $-2x_{S}+4y_{S}+k=0$, soit en remplaçant :

 

$-2\times 5+4\times (-1)+k=0\Rightarrow -14+k=0\Rightarrow k=14.$

 

Finalement, une équation de $(ST)$ est :

 

$-2x+4y+14=0$, soit en divisant par $(-2)$ :

 

$x-2y-7=0$, ou encore en transposant le terme en $y$ et en divisant par $2$ : 

 

$y=\dfrac{1}{2}x-\dfrac{7}{2}.$

 

Dans toutes les deux méthodes, la bonne réponse est donc la réponse 2)

 

5) La droite $(TR)$ a pour coefficient directeur :

 

$\dfrac{y_{R}-y_{T}}{x_{R}-x_{T}}=\dfrac{5-(-3)}{-3-1}=-2.$

 

La parallèle à $(TR)$ passant par $S$ a même coefficient directeur que $(TR)$ et par conséquent, son équation réduite est de la forme : 

 

$y=-2x+k.$ 

 

$S$ étant un point de cette droite, les coordonnées de $S$ doivent vérifier cette équation, d'où : 

 

$y_{S}=-2x_{S}+k$, ce qui s'écrit : 

 

$-1=-2\times 5+k\Rightarrow k=9.$

 

L'équation de la parallèle à $(TR)$ passant par $S$ est donc, finalement : 

 

$y=-2x+9.$

 

La bonne réponse est la réponse 3)

 

1) Chaque effectif partiel est proportionnel à l'angle au centre correspondant (propriété des diagrammes circulaires), en d'autres termes le rapport $\dfrac{\text{Effectif partiel}}{\text{Angle correspondant}}$ est une constante. 

 

Or, ce rapport vaut $\dfrac{45}{360^{\circ}}=\dfrac{1}{8}$, dans le cas de l'effectif total.

 

Par suite, on a les égalités suivantes :

 

$\begin{array}{lcl}\dfrac{\text{Nombre de chauffeurs}}{80^{\circ}}&=&\dfrac{\text{Nombre de commerciaux}}{72^{\circ}}\\&=&\dfrac{\text{Nombre de stylistes}}{24^{\circ}}\\&=&\dfrac{\text{Nombre de tailleurs}}{152^{\circ}}\\&=&\dfrac{\text{Nombre de gardiens}}{32^{\circ}}\\&=&\dfrac{1}{8}.\end{array}$

 

En utilisant l'égalité de ces rapports, on a facilement :

 

Nombre de chauffeurs=$80\times\dfrac{1}{8}=10.$

 

Nombre de commerciaux=$72\times\dfrac{1}{8}=9.$

 

Nombre de stylistes=$24\times\dfrac{1}{8}=3.$

 

Nombre de tailleurs=$152\times\dfrac{1}{8}=19.$

 

Nombre de gardiens=$32\times\dfrac{1}{8}=4.$

 

2) Le salaire moyen est donné par la somme des produits du salaire de chaque catégorie professionnelle par l'effectif partiel correspondant :

 

$\dfrac{(3\times 250\ 000)+(9\times 175\ 000)+(15\times 200\ 000)+(19\times 150\ 000)+(10\times 100\ 000)+(4\times 75\ 000)}{45}=210555.55$

1) Voir Figure ci-dessous :

 

 

 

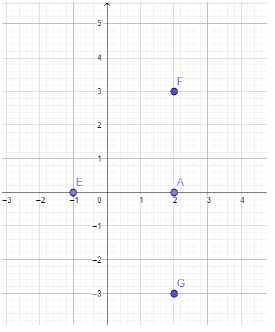
2) Il suffit de montrer, comme le suggère la figure, que les distances $EG$ et $EF$ sont égales et que les vecteurs $\overrightarrow{EG}$ et $\overrightarrow{EF}$ sont orthogonaux.

 

Or, d'après la formule donnant la distance entre deux points dans le plan muni d'un repère orthonormé, on a :

 

$\begin{array}{lcl}EG&=&\sqrt{(x_{G}-x_{E})^{2}+(y_{G}-y_{E})^{2}}\\&=&\sqrt{(2-(-1))^{2}+(-3 0)^{2}}\\&=&\sqrt{9+9}\\&=&\sqrt{18}\\&=&3\sqrt{2}.\end{array}$

 

$\begin{array}{lcl}\text{Et }EF&=&\sqrt{(x_{F}-x_{E})^{2}+(y_{F}-y_{E})^{2}}\\&=&\sqrt{(2-(-1))^{2}+(3-0)^{2}}\\&=&\sqrt{9+9}\\&=&\sqrt{18}\\&=&3\sqrt{2}.\end{array}$

 

Donc les distances $EG$ et $EF$ sont égales.

 

Calculons maintenant les coordonnées des vecteurs $\overrightarrow{EG}$ et $\overrightarrow{EF}$ et vérifions qu'ils sont orthogonaux.

 

On a :

 

$\overrightarrow{EG}\begin{pmatrix} x_{G}&-x_{E}\\ y_{G}&-y_{E} \end{pmatrix}$, soit $\overrightarrow{EG}\begin{pmatrix} 2&-(-1)\\ 3&-0 \end{pmatrix}$ ou encore  $\overrightarrow{EG}\begin{pmatrix} 3\\ -3 \end{pmatrix}$ et

 

$\overrightarrow{EF}\begin{pmatrix} x_{F}&-x_{E}\\ y_{F}&-y_{E} \end{pmatrix}$, soit $\overrightarrow{EF}\begin{pmatrix} 2&-(-1)\\ 3&-0 \end{pmatrix}$ ou encore $\overrightarrow{EF}\begin{pmatrix} 3\\ 3 \end{pmatrix}.$

 

On vérifie alors aisément que : 

 

$x_{\overrightarrow{EG}}\cdot x_{\overrightarrow{EF}}+y_{\overrightarrow{EG}}\cdot y_{\overrightarrow{EF}}=3\times 3+(-3)\times 3=0$ : 

 

Les vecteurs $\overrightarrow{EG}$ et $\overrightarrow{EF}$ sont orthogonaux et par conséquent les droites $(EF)$ et $(EG)$ sont perpendiculaires.

 

Il résulte de tout cela que le triangle $EFG$ est rectangle et isocèle en $E.$

 

3) Les points $E$ et $A$ étant tous deux situés sur l'axe des abscisses, car leurs ordonnées sont égales à $0$, l'axe $(EA)$ n'est autre que l'axe des abscisses. 

 

Pour montrer que les points $F$ et $G$ sont symétriques par rapport à cet axe, il suffit de vérifier qu'ils ont la même abscisse et des ordonnées opposées, ce qui est vrai d'après les données de l'énoncé, car ils ont pour abscisse $2$ et pour ordonnée $3$ et $-3.$

 

4) Puisque le triangle $EFG$ est rectangle et isocèle en $E$, il est clair que $EF=EG$ et que l'angle $\widehat{FEG}$ vaut $90^{\circ}.$

 

 

 

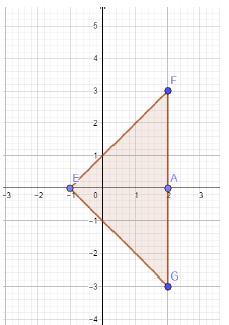
Par suite, l'angle de la rotation de centre $E$ qui applique $F$ sur $G$ est égal à $90^{\circ}.$

 

5) La rotation précédente est de sens indirect (sens des aiguilles d'une montre). 

 

L'image du point $G$ est le point $M$ de la figure ci-dessus, où $EGM$ est un triangle rectangle et isocèle en $M.$

 

 

 

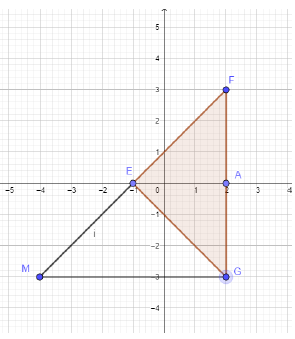
6) Il est clair, d'après les propriétés précédentes et en examinant la figure, que les points $F$ et $M$ sont symétriques par rapport à $E$, donc que le point $E$ est le milieu du segment $[FM].$

 

Les coordonnées de $E$ sont les demi-sommes des abscisses et des ordonnées des points $F$ et $M$ :

 

$E\begin{pmatrix}\dfrac{x_{F}+x_{M}}{2}\\ \dfrac{y_{F}+y_{M}}{2} \end{pmatrix}$, soit $E\begin{pmatrix}\dfrac{2+x_{M}}{2}\\ \dfrac{3+y_{M}}{2} \end{pmatrix}.$ 

 

Or, $E$ a pour coordonnées $(-1\;;\ 0)$ d'après l'énoncé, d'où les égalités :

 

$\left\lbrace\begin{array}{lcl} \dfrac{2+x_{M}}{2}&=&-1\\ \\ \dfrac{3+y_{M}}{2}&=&0 \end{array}\right.\ \Rightarrow\ $ $(2+x_{M}=-2)$ et $(3+y_{M}=2\times 0=0).$ 

 

On obtient aisément :

$$x_{M}=-4\text{ et }y_{M}=-3$$

 

Ce qui se vérifie d'ailleurs directement sur la figure.

1) Voir figure ci-dessous

 

 

 

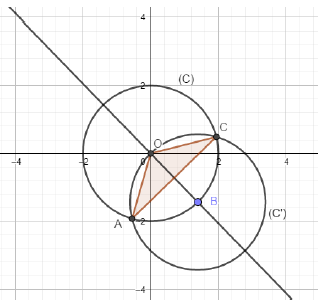
Justification de la figure : 

 

Prenons pour $B$ un point quelconque du cercle $(\mathcal{C})$ de centre $O$ et de rayon $2$, puis traçons le cercle $(\mathcal{C'})$ de centre $B$ et de rayon $2.$ 

 

Puisque $BC=OB=2$, $C$ est l'un des deux points d'intersection de $(\mathcal{C})$ et $(\mathcal{C'}).$ 

 

Désignons par $\mathcal{C}_{1}$ et $\mathcal{C}_{2}$ ces deux points. 

 

Le triangle $O\mathcal{C}_{1}\mathcal{C}_{2}$ est isocèle en $O.$ 

 

Si donc $C$ est l'un des points $\mathcal{C}_{1}$ ou $\mathcal{C}_{2}$, alors $A$ est l'autre point car $(OB)$ doit être la bissectrice de $\widehat{AOC}$ et $A$ doit être sur le cercle $(\mathcal{C}).$

 

2) D'après les hypothèses de l'énoncé, on a $OB=BC=OC=2\;cm$, donc le triangle est équilatéral. 

 

Chacun de ses angles vaut donc $60^{\circ}$ et on a bien : 

 

$\widehat{OBC}=\widehat{OCB}=\widehat{BOC}=60^{\circ}.$

 

3) Voir figure ci-dessous.

 

L'angle $\widehat{CAB}$ est un angle inscrit dans le cercle $(\mathcal{C})$ qui a pour angle au centre correspondant $\widehat{BOC}.$ 

 

Il résulte du théorème de l'angle inscrit et de la question précédente que :

$$\widehat{CAB}=\dfrac{1}{2}\widehat{BOC}=\dfrac{1}{2}\times 60^{\circ}=30^{\circ}.$$

 

De même : 

 

$\widehat{BCA}=\dfrac{1}{2}\widehat{BOA}=\dfrac{1}{2}\times 60^{\circ}=30^{\circ}.$ 

 

(On a $\widehat{BOA}=\widehat{BOC}=60^{\circ}$ car, par hypothèse, $(OB)$ est la bissectrice de $\widehat{AOC}.$

 

 

 

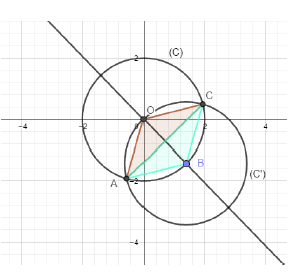
Enfin, pour calculer le dernier angle $\widehat{ABC}$ du triangle $ABC$, on peut :
 

- soit remarquer qu'il s'agit d'un angle inscrit dans le cercle $(\mathcal{C})$ qui intercepte le même arc que l'angle au centre rentrant $\overset{\displaystyle\smile}{COA}$ de ce cercle et puisque $\widehat{COA}=2\times 60^{\circ}=120^{\circ}$, on a : 

 

$\overset{\displaystyle\smile}{COA}=360^{\circ}-120^{\circ}=240^{\circ}.$

 

Le théorème de l'angle inscrit entraîne alors que : 

 

$\widehat{ABC}=\dfrac{1}{2}\overset{\displaystyle\smile}{COA}\times 240^{\circ}= 120^{\circ}.$

 

- soit, tout simplement appliquer le théorème sur la somme des angles d'un triangle :

$$\widehat{ABC}+\widehat{BCA}+\widehat{BAC}=180^{\circ}$$ et d'après les calculs précédemment effectués, on a $\widehat{BCA}=\widehat{BAC}=30^{\circ}$, d'où : $$\widehat{ABC}=180^{\circ}-(30^{\circ}+30^{\circ})=120^{\circ}.$$