Corrigé BFEM Physique Chimie 2013

 

Exercice 1

Une solution d'acide chlorhydrique $(H^{+}+Cl^{-})$ de concentration molaire $C=2\cdot 10^{-1}\;mol.L^{-1}$  est obtenue par dissolution d'un volume $V$ de gaz chlorhydrique dans $200\;mL$ d'eau pure.
 
1.1) Déterminons en $g.L^{-1}$ la concentration massique $C_{m}$ de la solution
 
Soit : $C_{m}=C\times M$ avec,
 
$\begin{array}{rcl} M(HCl)&=&M(H)+M(Cl)\\ \\&=&1+35.5\\ \\&=&36.5\end{array}$
 
Donc, $M(HCl)=36.5\;g.mol^{-1}$
 
Par suite, $C_{m}=2\cdot 10^{-1}\times 36.5=7.3$
 
D'où,
$$\boxed{C_{m}=7.3\;g.L^{-1}}$$
1.2)Calculons le volume $V$ de gaz chlorhydrique dissout
 
On a : $n=\dfrac{V}{V_{M}}\ \Rightarrow\ V=n\times V_{M}$

Or, $n=C\times V_{s}$ où $V_{s}$ est le volume de la solution
 
Donc en remplaçant $n$ par $C\times V_{s}$, on obtient :
$$V=C\times V_{s}\times V_{M}$$
A.N : $V=2\cdot 10^{-1}\times 200\cdot 10^{-3}\times 22.4=0.896$
 
Ainsi,
$$\boxed{V=0.896\;L=896\;mL}$$
1.3) On fait réagir les $200\;ml$ de la solution d'acide sur de la poudre de zinc en excès.
 
1.3.1) Écrivons l'équation-bilan ionique de la réaction
$$2(H^{+}+Cl^{-})\ +\ Zn^{2+}\ \longrightarrow\ (Zn^{2+}+2Cl^{-})\ +\ 2H^{+}$$ 
1.3.2) Trouvons le volume de dihydrogène dégagé.
 
D'après l'équation, on a :
 
$\begin{array}{rcl}\dfrac{n_{_{(H^{+}+Cl^{-})}}}{2}=\dfrac{n_{_{(H^{+})}}}{2}&\Rightarrow&n_{_{(HCl)}}=n_{_{(H_{2})}}\\ \\&\Rightarrow&\dfrac{V}{V_{M}}=\dfrac{V_{_{(H_{2})}}}{V_{M}}\\ \\&\Rightarrow&V_{_{(H_{2})}}=V\end{array}$
 
Par suite,
$$\boxed{V(H_{2})=0.896\;L}$$

Exercice 2

l'acétylène $(C_{2}H_{2})$ est un hydrocarbure utilisé dans la soudure métallique. Sa combustion dégage beaucoup de chaleur.

Pour souder une porte en fer, un menuisier métallique utilise $2.6\;kg$ de ce gaz.
 
2.1) Trouvons la quantité de matière d'acétylène utilisée
 
Soit : $n=\dfrac{m}{M}$ avec 
 
$\begin{array}{rcl} M(C_{2}H_{2})&=&2M(C)+2M(H)\\ \\&=&2\times 12+2\times 1\\ \\&=&24+2\\ \\&=&26\end{array}$
 
Donc, $M(C_{2}H_{2})=26\;g.mol^{-1}$
 
Par suite, $n=\dfrac{2.6\cdot 10^{3}}{26}=100$
 
D'où,
$$\boxed{n=100\;mol}$$
2.2) Écrivons l'équation-bilan de la complète de l'acétylène
$$C_{2}H_{2}\ +\ \dfrac{5}{2}O_{2}\ \longrightarrow\ 2CO_{2}\ +\ H_{2}O$$
2.3) Calculons le volume d'air nécessaire à la combustion
 
D'après l'équation, on a :
 
$\begin{array}{rcl}\dfrac{n_{_{(C_{2}H_{2})}}}{1}=\dfrac{n_{_{(O_{2})}}}{\dfrac{5}{2}}&\Rightarrow&5n_{_{(C_{2}H_{2})}}=2n_{_{(O_{2})}}\\ \\&\Rightarrow&n_{_{(O_{2})}}=\dfrac{5n_{_{(C_{2}H_{2})}}}{2}\\ \\&\Rightarrow&n_{_{(O_{2})}}=\dfrac{5\times100}{2}\\ \\&\Rightarrow&n_{_{(O_{2})}}=250\;mol\end{array}$
 
Par ailleurs, $n_{_{(O_{2})}}=\dfrac{V_{_{(O_{2})}}}{V_{M}}$
 
Ce qui donne : $V_{_{(O_{2})}}=n_{_{(O_{2})}}\times V_{M}$
 
Comme $V_{_{(O_{2})}}=\dfrac{1}{5}V_{\text{air}}$ alors,
$$V_{\text{air}}=5V_{_{(O_{2})}}=5\times n_{_{(O_{2})}}\times V_{M}$$
A.N : $V_{\text{air}}=5\times 250\times 24=30\,000$
 
D'où,
$$\boxed{V_{\text{air}}=30\,000\;L}$$

Exercice 3

La vergence d'une lentille convergente $C=50$ dioptries.
 
Un objet $AB$ d'une hauteur $h=2\;cm$ est placé à $4\;cm$ du centre optique de la lentille. L'objet $AB$ est placé perpendiculairement à l'axe optique principal de la lentille, le point $A$ étant sur cet axe.
 
3.1) Calculons la distance focale de la lentille
 
Pour une lentille convergente, on a :
$$C=\dfrac{1}{f}\ \Rightarrow\ C\times f=1$$
D'où, $f=\dfrac{1}{C}$
 
A.N : $f=\dfrac{1}{50}=0.02$
 
Donc, $$\boxed{f=0.02\;m=2\;cm}$$
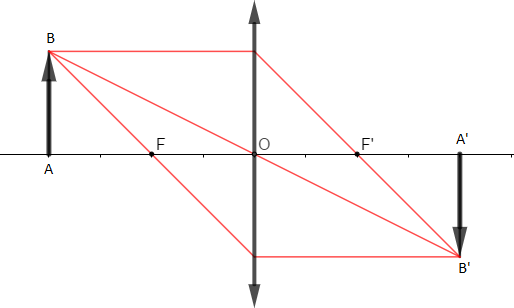
3.2) Construisons l'image $A'B'$ de l'objet $AB$ et donnons la position et la hauteur de cette image
 
 
L'image est de l'autre côté de la lentille.
 
Sa hauteur $h'$ est égale à : $$\boxed{h'=A'B'=2\;cm}$$

Exercice 4

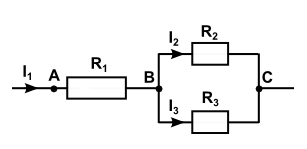
On considère la portion de circuit schématisé ci-dessous :
 
 
On donne : 
 
$U_{AC}=30\;V\;;\ R_{1}=5\;\Omega\;;\ R_{2}=R_{3}=10\;\Omega$
 
4.1) Calculons la résistance équivalente à l'ensemble des résistances $R_{1}\;,\ R_{2}\ $ et $\ R_{3}$
 
Soit $R_{AC}$ équivalente à l'ensemble des résistances.
 
On a : $R_{AC}=R_{AB}+R_{BC}$ avec $R_{AB}=R_{1}$
 
Comme $R_{2}\ $ et $\ R_{3}$ sont en dérivation alors, leur résistance équivalente $R_{BC}$ vérifie :
$$\dfrac{1}{R_{BC}}=\dfrac{1}{R_{2}}+\dfrac{1}{R_{3}}=\dfrac{R_{2}+R_{3}}{R_{2}\times R_{3}}$$
Par suite, $R_{BC}=\dfrac{R_{2}\times R_{3}}{R_{2}+R_{3}}$
 
En remplaçant, on obtient alors :
$$R_{AC}=R_{1}+\dfrac{R_{2}\times R_{3}}{R_{2}+R_{3}}$$
A.N : $R_{AC}=5+\dfrac{10\times 10}{10+10}=5+5=10$
 
D'où, $$\boxed{R_{AC}=10\;\Omega}$$
 
4.2) Calculons les intensités des courants $I_{1}, I_{2}\ $ et $\ I_{3}$
 
En effet, le courant $I_{1}$ traverse la résistance $R_{AC}$ équivalente à l'ensemble.
 
Donc, d'après la loi d'Ohm, on a :
$$U_{AC}=R_{AC}\times I_{1}$$
Ce qui donne : $I_{1}=\dfrac{U_{AC}}{R_{AC}}$
 
A.N : $I_{1}=\dfrac{30}{10}=3$
 
D'où, $$\boxed{I_{1}=3\;A}$$
Par ailleurs, d'après la loi des nœuds, on a :
$$I_{1}=I_{2}+I_{3}$$
Comme $R_{2}=R_{3}$ alors, $I_{2}=I_{3}$
 
Par suite, $I_{2}=I_{3}=\dfrac{I_{1}}{2}$
 
A.N : $I_{2}=I_{3}=\dfrac{3}{2}=1.5$
 
Ainsi, $$\boxed{I_{2}=I_{3}=1.5\;A}$$
4.3) Déterminons la tension aux bornes de chaque résistance
 
D'après la loi d'Ohm, on a :
 
$U_{1}=U_{AB}=R_{1}\times I_{1}$
 
A.N : $U_{1}=5\times 3=15$
 
Donc, $$\boxed{U_{1}=15\;V}$$
De la même manière : $U_{2}=R_{2}\times I_{2}$
 
A.N : $U_{2}=10\times 1.5=15$
 
D'où, $$\boxed{U_{2}=15\;V}$$
Enfin, comme $R_{2}\ $ et $\ R_{3}$ sont en parallèle alors, $U_{2}=U_{3}$
 
D'où, $$\boxed{U_{3}=15\;V}$$

Commentaires

mo (non vérifié)

dim, 08/01/2021 - 15:08

pourquoi vous n'avez pas corrigé la partie physique?

Anonyme (non vérifié)

jeu, 08/05/2021 - 18:49

Nous nous voulons l'exercice 4 ms pas ça

amadi (non vérifié)

lun, 11/06/2023 - 21:41

Aidez moi c'est la que je trouve des solutions concrètes

Ajouter un commentaire