Corrigé BFEM Physique chimie 2015
Exercice 1
La vitamine $C$ est un médicament utilisé en particulier contre la fatigue. Sa formule brute est $C_{6}H_{8}O_{6}.$
Un comprimé contient une masse $m=500\;mg$ de vitamine $C.$
1.1) Calculons la masse molaire $M_{(C_{6}H_{8}O_{6})}$ de la vitamine $C$
On a :
$\begin{array}{rcl} M_{(C_{6}H_{8}O_{6})}&=&M_{(C_{6})}+M_{(H_{8})}+M_{(O_{6})}\\\\&=&6M_{(C)}+8M_{(H)}+6M_{(O)}\\\\&=&6\times 12+8\times 1+6\times 16\\\\&=&72+8+96\\\\&=&176\end{array}$
Donc, $$\boxed{ M_{(C_{6}H_{8}O_{6})}=176\;g.mol^{-1}}$$
1.2) On prépare une solution en dissolvant un comprimé de vitamine C dans $250\;mL$ d'eau pure. La dissolution s'est faite sans changement de volume.
1.2.1) Calculons la quantité de matière de vitamine $C$ dans la solution.
Soit : $n_{(C_{6}H_{8}O_{6})}=\dfrac{m}{M_{(C_{6}H_{8}O_{6})}}$
A.N : $n_{(C_{6}H_{8}O_{6})}=\dfrac{500\cdot 10^{-3}}{176}=2.84\cdot 10^{-3}$
Ainsi, $$\boxed{n_{(C_{6}H_{8}O_{6})}=2.84\cdot 10^{-3}\;mol}$$
1.2.2) Calculons la molarité de la solution :
Soit : $C=\dfrac{n_{(C_{6}H_{8}O_{6})}}{V}$
A.N : $C=\dfrac{2.84\cdot 10^{-3}}{250\cdot 10^{-3}}=1.136\cdot10^{-2}$
D'où, $$\boxed{C=1.136\cdot 10^{-2}\;mol.L^{-1}}$$
En déduisons sa concentration massique :
Soit : $C_{m}=C\times M_{(C_{6}H_{8}O_{6})}$
A.N : $C_{m}=1.136\cdot 10^{-2}\times 176=2$
Donc, $$\boxed{C_{m}=2\;g.L^{-1}}$$
Exercice 2
La molécule d'un alcane possède $6$ atomes d'hydrogène.
2.1) Écrivons la formule brute de cet alcane et donnons son nom :
La formule générale d'un alcane étant $C_{n}H_{2n+2}$ alors, un alcane qui possède $6$ atomes d'hydrogène signifie :
$$H_{2n+2}=H_{6}$$
Soit alors :
$\begin{array}{rcl} 2n+2=6&\Rightarrow& 2n=6-2\\\\&\Rightarrow&2n=4\\\\&\Rightarrow&2n=\dfrac{4}{2}\\\\&\Rightarrow&n=2\end{array}$
En remplaçant cette valeur de $n$ dans l'expression de la formule générale d'un alcane, on obtient : $C_{2}H_{6}$
Donc, la formule brute de l'alcane est :
$$C_{2}H_{6}$$
Son nom est : éthane
2.2) La combustion complète de cet alcane a nécessité $2.5\;L$ de dioxygène.
2.2.1) Écrivons l'équation bilan de cette réaction de combustion
$$C_{2}H_{6}\ +\ \dfrac{7}{2}O_{2}\ \longrightarrow\ 2CO_{2}\ +\ 3H_{2}O$$
2.2.2) Calculons la masse d'alcane qui a réagi au cours de cette combustion
Soit : $m_{(C_{2}H_{6})}=n_{(C_{2}H_{6})}\times M_{(C_{2}H_{6})}$
avec
$\begin{array}{rcl} M_{(C_{2}H_{6})}&=&2M_{(C)}+6M_{(H)}\\\\&=&2\times 12+6\times 1\\\\&=&24+6\\\\&=&30\end{array}$
Ainsi, $M_{(C_{2}H_{6})}=30\;g.mol^{-1}$
D'après l'équation bilan, on a : $\dfrac{n_{(C_{2}H_{6})}}{1}=\dfrac{n_{(O_{2})}}{\dfrac{7}{2}}$
Or, $n_{(O_{2})}=\dfrac{V_{(O_{2})}}{V_{M}}$
Donc, $\dfrac{n_{(C_{2}H_{6})}}{1}=\dfrac{\dfrac{V_{(O_{2})}}{V_{M}}}{\dfrac{7}{2}}$
Par suite, $n_{(C_{2}H_{6})}=\dfrac{2}{7}\times\dfrac{V_{(O_{2})}}{V_{M}}$
Ainsi, en remplaçant cette expression de $n_{(C_{2}H_{6})}$ dans l'expression de la masse, on obtient :
$\begin{array}{rcl} m_{(C_{2}H_{6})}&=&\dfrac{2}{7}\times\dfrac{V_{(O_{2})}}{V_{M}}\times M_{(C_{2}H_{6})}\\\\&=&\dfrac{2\times V_{(O_{2})}\times M_{(C_{2}H_{6})}}{7\times V_{M}}\end{array}$
A.N : $m_{(C_{2}H_{6})}=\dfrac{2\times 2.5\times 30}{7\times 25}=0.857$
D'où, $$\boxed{m_{(C_{2}H_{6})}=0.857\;g}$$
2.2.3) Trouvons le volume de dioxyde de carbone formé
On a : $n_{(CO_{2})}=\dfrac{V_{(CO_{2})}}{V_{M}}$
Ce qui donne : $V_{(CO_{2})}=n_{(CO_{2})}\times V_{M}$
Or, d'après l'équation bilan, on a : $\dfrac{n_{(CO_{2})}}{2}=\dfrac{n_{(O_{2})}}{\dfrac{7}{2}}\ \Rightarrow\ n_{(CO_{2})}=\dfrac{2\times 2\times n_{(O_{2})}}{7}$
Or, $n_{(O_{2})}=\dfrac{V_{(O_{2})}}{V_{M}}$ donc,
$\begin{array}{rcl} n_{(CO_{2})}&=&\dfrac{2\times 2\times\dfrac{V_{(O_{2})}}{V_{M}}}{7}\\\\&=&\dfrac{\dfrac{4\times V_{(O_{2})}}{V_{M}}}{7}\\\\&=&\dfrac{4\times V_{(O_{2})}}{7\times V_{M}}\end{array}$
Par suite, le volume de dioxyde de carbone formé est donné par :
$\begin{array}{rcl} V_{(CO_{2})}&=&n_{(CO_{2})}\times V_{M}\\\\&=&\dfrac{4\times V_{(O_{2})}}{7\times V_{M}}\times V_{M}\\\\&=&\dfrac{4\times V_{(O_{2})}}{7}\end{array}$
A.N : $V_{(CO_{2})}=\dfrac{4\times 2.5}{7}=1.428$
Donc, $$\boxed{V_{(CO_{2})}=1.428\;L}$$
Exercice 3
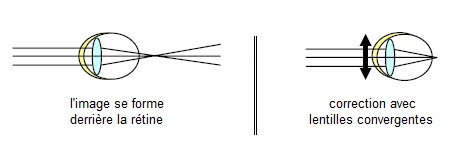
3.1) Le cristallin de l'œil se comporte comme une lentille convergente. L'acuité visuelle de l'homme s'affaiblit généralement à partir de $40\;ans.$ Le foyer image du cristallin se trouve alors derrière la rétine.
3.1.1) L'œil est atteint de presbytie
3.1.2) Représentons sur un schéma les rayons lumineux qui traversent le cristallin de l'œil.

$\text{Rayons lumineux traversant}$
$\text{le cristallin de l'œil presbyte}$
3.1.3) A la visite médicale, l'ophtalmologue prescrit au patient des verres correcteurs.
Le cristallin de l'œil se comporte comme une lentille convergente. En effet, un affaiblissement de sa convergence impacte directement la vision.
Donc pour corriger une telle anomalie on doit renforcer la convergence.
Ce qui veut dire qu'on doit utiliser des verres constitués de lentilles convergentes.
3.2) Une lentille convergente a une vergence $C=10\;\delta$.
3.2.1)calculons la distance focale $f$
On sait que : $C=\dfrac{1}{f}$
Ce qui donne alors, $f=\dfrac{1}{C}$
A.N : $f=\dfrac{1}{10}=0.1$
Donc, $$\boxed{f=0.1\;m}$$
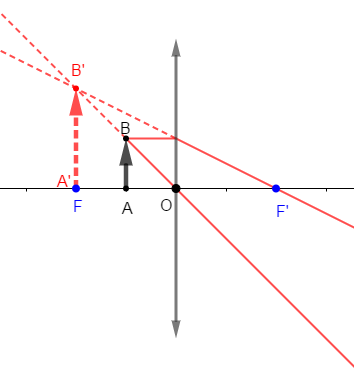
3.2.2) Construisons à l'échelle $\dfrac{1}{5}$ l'image $A'B'$ de l'objet $AB$
Donc, sur la figure, $1\;cm$ représente $5\;cm$

Donnons les caractéristiques de l'image :
$-\ $ nature : virtuelle
$-\ $ sens : droite
$-\ $ position : du même côté que l'objet
$-\ $ taille : plus grande que l'objet
$-\ $ agrandissement : $\gamma=\dfrac{A'B'}{AB}=\dfrac{10}{5}=2$
Exercice 4
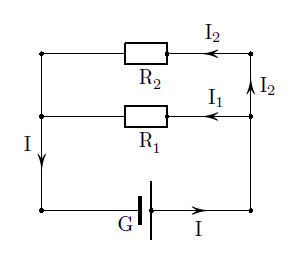
Un circuit électrique est constitué d'un générateur relié à deux résistors de résistances respectives $R_{1}=30\;\Omega\ $ et $\ R_{2}$ inconnue. La résistance équivalente à l'association est $R_{eq}=12\;\Omega.$
4.1) Les résistors sont montés en dérivation.
En effet, pour un montage en série, la résistance équivalente est égale à la somme de toutes les résistances : $R_{eq}=R_{1}+R_{2}$
Dans de telles conditions, $R_{eq}$ est plus grand que $R_{1}\ $ et $\ R_{2}.$
Or, nous constatons que $R_{eq}<R_{1}.$
Donc, les résistors ne sont pas en série.
Par conséquent, ils sont montés en dérivation.
4.2) Trouvons la valeur de $R_{2}$
Pour un montage en dérivation, on a :
$\begin{array}{rcl}\dfrac{1}{R_{eq}}=\dfrac{1}{R_{1}}+\dfrac{1}{R_{2}}&\Rightarrow&\dfrac{1}{R_{2}}=\dfrac{1}{R_{eq}}-\dfrac{1}{R_{1}}\\\\&\Rightarrow&\dfrac{1}{R_{2}}=\dfrac{R_{1}-R_{eq}}{R_{1}\times R_{eq}}\\\\&\Rightarrow&R_{2}=\dfrac{R_{1}\times R_{eq}}{R_{1}-R_{eq}}\end{array}$
Ainsi, $\boxed{R_{2}=\dfrac{R_{1}\times R_{eq}}{R_{1}-R_{eq}}}$
A.N : $R_{2}=\dfrac{30\times12}{30-12}=\dfrac{360}{18}=20$
D'où, $$\boxed{R_{2}=20\;\Omega}$$
4.3) Représentons le circuit électrique

4.4) le générateur débite un courant d'intensité $I=500\,mA$.
4.4.1) Calculons la tension entre les bornes du générateur
D'après la loi d'Ohm, on a :
$$U=R_{eq}\times I$$
A.N : $U=12\times500\cdot10^{-3}=6$
D'où, $$\boxed{U=6\;V}$$
4.4.2) Déterminons la valeur de l'intensité du courant qui parcourt chaque résistor
Notons que dans un circuit en dérivation, la tension est la même dans chaque branche :
$$U=U_{1}=U_{2}$$
Ainsi,
$-\ $ Pour $R_{1}$, on obtient :
$\begin{array}{rcl} U_{1}=R_{1}\times I_{1}&\Rightarrow&I_{1}=\dfrac{U_{1}}{R_{1}}\\\\&\Rightarrow&I_{1}=\dfrac{U}{R_{1}}\end{array}$
Donc, $\boxed{I_{1}=\dfrac{U}{R_{1}}}$
A.N : $I_{1}=\dfrac{6}{30}=0.2$
Ainsi, $$\boxed{I_{1}=0.2\;A=200\;mA}$$
$-\,$ Pour $R_{2}$, on a :
$\begin{array}{rcl} U_{2}=R_{2}\times I_{2}&\Rightarrow&I_{2}=\dfrac{U_{2}}{R_{2}}\\\\&\Rightarrow&I_{2}=\dfrac{U}{R_{2}}\end{array}$
Ainsi, $\boxed{I_{2}=\dfrac{U}{R_{2}}}$
A.N : $I_{2}=\dfrac{6}{20}=0.3$
D'où, $$\boxed{I_{2}=0.3\;A=300\;mA}$$
Auteur:
Aliou ndiaye

Commentaires
Sagne (non vérifié)
dim, 08/01/2021 - 02:16
Permalien
C'est génial
Ajouter un commentaire