Corrigé BFEM Physique chimie 2016

Exercice 1

1) Déterminons la concentration massique

On a :

$c_{m}=\dfrac{m}{V}\$ avec

$\ m=n\times M$

Donc,

$c_{m}=\dfrac{n\times M}{V}\$ or

$\ \dfrac{n}{V}=c$

D'où,

$c_{m}=c\times M\$ avec

$M_{(HCl)}=1+35.5=36.5\;g.mol^{-1}$

A.N :

$c_{m}=2\;10^{-1}\times 36.5=7.3$

Donc,

$\boxed{c_{m}=7.3\;g.l^{-1}}$

2) Calculons la concentration molaire de

$NaOH$

Soit

$A$ la solution de

$HCl$ et

$B$ la solution de

$NaOH$

A l'équivalence on a :

$n_{A}=n_{B}\$ or

$n=c\times V$

Donc,

$c_{A}V_{A}=c_{B}V_{B}$

D'où,

$c_{B}=\dfrac{c_{A}V_{A}}{V_{B}}$

A.N :

$c_{B}=\dfrac{2\;10^{-1}\times 80}{40}=0.4$

Donc,

$\boxed{c_{B}=0.4\;mol.l^{-1}}$

3) On verse

$120\;ml$ de

$HCl$ dans du zinc.

3) 1) Écrivons l'équation bilan. On a :

$2HCl\ +\ Zn \longrightarrow\ ZnCl_{2}\ +\ H_{2}$

3) 2) Trouvons le volume de

$H_{2}$ dégagé.

On a du

$Zn$ en excès, donc toute la quantité de

$HCl$ a réagi.

D'après l'équation ci-dessus, on a :

$\dfrac{n_{(HCl)}}{2}=\dfrac{n_{(H_{2})}}{1}$

Donc,

$n_{(HCl)}=2n_{(H_{2})}\$ or

$\ n=cV=\dfrac{V}{V_{M}}$

Ainsi,

$c_{(HCl)}V_{(HCl)}=2\dfrac{V_{(H_{2})}}{V_{M}}$

D'où,

$V_{(H_{2})}=\dfrac{c_{(HCl)}\times V_{(HCl)}\times V_{M}}{2}$

A.N :

$V_{(H_{2})}=\dfrac{2\;10^{-1}\times 120\;10^{-3}\times 22.4}{2}=0.2688$

Donc,

$\boxed{V_{(H_{2})}=268.8\;ml}$

Exercice 2

1) Le méthane appartient à la famille des alcanes.

2) Écrivons la formule générale de cette famille.

Soit un alcane

$A$ de

$n$ atomes de carbones, alors

$A$ est de la forme

$C_{n}H_{2n+2}$

3) Équation bilan complète de la combustion complète du méthane.

$CH_{4}\ +\ 2O_{2} \longrightarrow\ CO_{2}\ +\ 2H_{2}O$

4) Calculons le volume de

$O_{2}$ nécessaire.

D'après l'équation bilan on a :

$\dfrac{n_{(CH_{4})}}{1}=\dfrac{n_{(O_{2})}}{2}$ or

$n=\dfrac{m}{M}=\dfrac{V}{V_{M}}$

Donc,

$\dfrac{m_{(CH_{4})}}{M_{(CH_{4})}}=\dfrac{V_{(O_{2})}}{2V_{M}}\$ or

$M_{(CH_{4})}=12+4=16\;g.mol^{-1}$

Alors on aura :

$V_{(O_{2})}=\dfrac{m_{(CH_{4})}\times 2V_{M}}{M_{(CH_{4})}}$

A.N :

$V_{(O_{2})}=\dfrac{320\times 2\times 24}{16}=960$

Donc,

$\boxed{V_{(O_{2})}=960\;l}$

5) Trouvons la masse de

$CO_{2}$ formée.

D'après l'équation bilan de la question 3) on a :

$\dfrac{n_{(CH_{4})}}{1}=\dfrac{n_{(CO_{2})}}{1}$ or

$n=\dfrac{m}{M}$

Donc,

$\dfrac{m_{(CH_{4})}}{M_{(CH_{4})}}=\dfrac{m_{(CO_{2})}}{M_{(CO_{2})}}\$ avec

$M_{(CH_{4})}=16\;g.mol^{-1}$ et

$M_{(CO_{2})}=12+2\times 16=44\;g.mol^{-1}$

Alors on aura :

$m_{(CO_{2})}=\dfrac{m_{(CH_{4})}\times M_{(CO_{2})}}{M_{(CH_{4})}}$

A.N :

$m_{(CO_{2})}=\dfrac{320\times 44}{16}=880$

Donc,

$\boxed{m_{(CO_{2})}=880\;g}$

Exercice 3

1) Calculons la distance focale

On a :

$v=\dfrac{1}{f}$ , donc

$f=\dfrac{1}{v}$

A.N :

$f=\dfrac{1}{40}=0.025$

Donc,

$\boxed{f=2.5\;cm}$

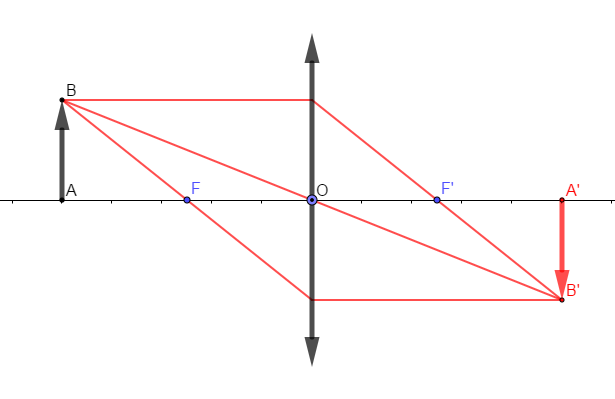
2) Construisons l'image

$A'B'$ de l'objet

$AB$

3) Déterminons :

$-\$ la hauteur

$A'B'$

On a :

$A'B'=2\;cm$

$-\$ la distance

$OA$

On a :

$OA=5\;cm$

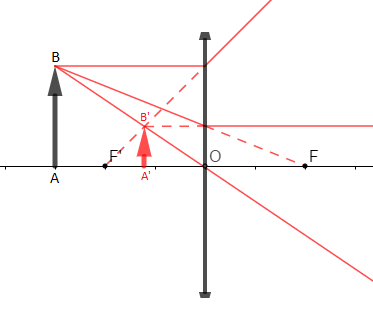
4) Construisons l'image de ce même objet par une lentille divergente.

Exercice 4

1) Énonçons la loi de Joule

La quantité de chaleur dégagée dans un conducteur par le passage d'un courant électrique est :

$-\$ proportionnelle au temps

$t$ de passage du courant.

$-\$ proportionnelle au carré de l'intensité

$I$ du courant.

$-\$ variable avec la résistance

$R$ du conducteur.

On a :

$E=W=R.I^{2}.t$

2) Calculons

$R_{1}$

D'après la loi de Joule on a :

$E=R_{1}I^{2}t$

Alors,

$R_{1}=\dfrac{E}{I^{2}t}$

A.N :

$R_{1}=\dfrac{60\;10^{3}}{2^{2}\times 5\times 60}=50$

Donc,

$\boxed{R_{1}=50\;\Omega}$

3) Calculons la tension

$U$

On a :

$U=R_{1}I$

A.N :

$U=50\times 2=100$

Donc,

$\boxed{U=100\;V}$

4) 1) Les conducteurs de résistances

$R_{1}$ et

$R_{2}$ sont montés en parallèles car la résistance équivalente est inférieure à

$R_{1}.$

Par ailleurs, si les conducteurs étaient montés en série, alors la résistance équivalente

$(R_{eq}=R_{1}+R_{2})$ serait supérieure à

$R_{1}.$

4) 2) Calculons

$R_{2}$

On a :

$\dfrac{1}{R_{eq}}=\dfrac{1}{R_{1}}+\dfrac{1}{R_{2}}$

alors on aura :

$\dfrac{1}{R_{2}}=\dfrac{1}{R_{eq}}-\dfrac{1}{R_{1}}=\dfrac{R_{1}-R_{eq}}{R_{eq}R_{1}}$

donc,

$R_{2}=\dfrac{R_{eq}R_{1}}{R_{1}-R_{eq}}$

A.N :

$R_{1}=\dfrac{50\times 20}{50-20}=33.333$

Ainsi,

$\boxed{R_{2}=33.333\;\Omega}$

Auteur:

Aliou ndiaye

Commentaires

Assane (non vérifié)

dim, 05/05/2019 - 14:51

Permalien

Site pédagogique très utile

répondre

Anonyme (non vérifié)

mar, 07/16/2019 - 21:09

Permalien

C'est bon pour moi

répondre

Anonyme (non vérifié)

mar, 05/26/2020 - 02:33

Permalien

excusez moi mais je pense qu

excusez moi mais je pense qu'au niveau de l'exo 3 la hauteur de A'B' est de 2cm car AO est egale a deux fois la distance focale

répondre

fdini

mar, 05/26/2020 - 05:38

Permalien

merci pour le retour, ct une

merci pour le retour, ct une faute de frappe mais on l'a corrigé

répondre

Anonyme (non vérifié)

ven, 07/09/2021 - 06:10

Permalien

Au niveau de l'exercice 1on

Au niveau de l'exercice 1on constate une erreur qui est la suivante M(HCL)=1+35,5=35,6

répondre

Anonyme (non vérifié)

ven, 07/16/2021 - 23:40

Permalien

C'est bien ça35,5+1=36,5

répondre

Moustephe (non vérifié)

jeu, 08/05/2021 - 13:27

Permalien

Au niveau de l'éxo 2 vous n

Au niveau de l'éxo 2 vous n'avez op calculer le nombre de mol pourquoi?

répondre

Ajouter un commentaire

form.antibot { display: none !important; } You must have JavaScript enabled to use this form.

Vous êtes ici

Corrigé BFEM Physique chimie 2016

Formulaire de recherche

Exercice 1

Exercice 2

Exercice 3

Exercice 4

Commentaires

Site pédagogique très utile

C'est bon pour moi

excusez moi mais je pense qu

merci pour le retour, ct une

Au niveau de l'exercice 1on

C'est bien ça35,5+1=36,5

Au niveau de l'éxo 2 vous n

Ajouter un commentaire

Plain text