Symétrie orthogonale par rapport à une droite donnée - 6e
Classe:
Sixième
Activité
1) Plie une feuille de papier en deux.
2) A l'aide de la pointe de ton compas, fais un petit trou à travers les deux parties de la feuille.
3) Déplie la feuille. Note $C\ $ et $\ D$ les points déterminés par les deux trous obtenus.
4) Dessine $(\Delta)$ la droite obtenue en passant par la ligne de pliage.
Que représente $(\Delta)$ pour le segment $[CD]\ ?$
5) Où se trouve le point $D$ si le point $C$ est sur la droite $(\Delta)\ ?$
Les points $C\ $ et $\ D$ sont symétriques par rapport à la droite $(\Delta).$
Solution
1) 2) Plions une feuille de papier en deux puis à l'aide de la pointe de ton compas, faisons un petit trou à travers les deux parties de la feuille.
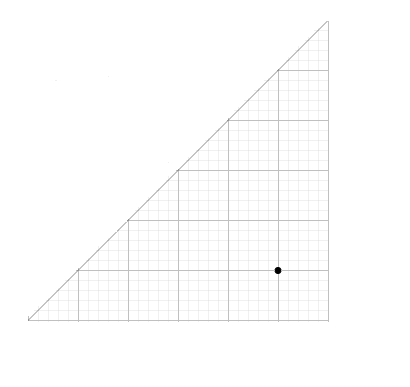
3) Déplions la feuille puis notons $C\ $ et $\ D$ les points déterminés par les deux trous obtenus.
4) Dessinons $(\Delta)$ la droite obtenue en passant par la ligne de pliage.
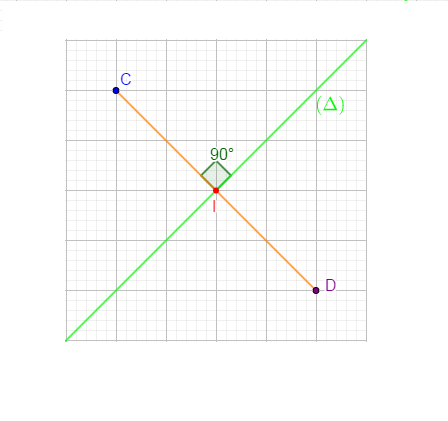
$-\ $ Le résultat de l'activité montre que $(\Delta)$ est perpendiculaire au segment $[CD].$
$-\ $ Avec mon compas je vérifie que $CI=DI$ avec $I$ le point de rencontre de $(\Delta)\ $ et $\ [CD]\ :$
$(\Delta)$ est la médiatrice du segment $[CD].$
$-\ $ On dit alors que $C$ est le symétrique de $D$ par rapport à $(\Delta)$ ou $D$ est le symétrique de $C$ par rapport à $(\Delta).$
I. Points symétriques par rapport à une droite
I.1. Définition
Soit $(\mathcal{D})$ une droite donnée du plan et $M$ un point de ce plan.
On dit que $M'$ est le symétrique de $M$ par rapport à la droite $(\mathcal{D})$ lorsque la droite $(\mathcal{D})$ est la médiatrice de $[MM'].$
I.2. Vocabulaire
On peut dire que :
$-\ $ Le point $M'$ est le symétrique de $M$ par rapport à la droite $(\mathcal{D})$
$-\ $ Les points $M\ $ et $\ M'$ sont symétriques par rapport à la droite $(\mathcal{D}).$
I.3. Notation
On note :
$$s_{(\mathcal{D})}(M)=M'$$
I.4 Construction à la règle et à l'équerre
Je trace la droite $(\mathcal{D})$ puis je place le point $M.$
Je trace la perpendiculaire à $(\mathcal{D})$ passant par $M.$ Cette droite coupe $(\mathcal{D})$ en $I.$
Je place le point $M'$ tel que $I$ soit le milieu de $[MM'].$
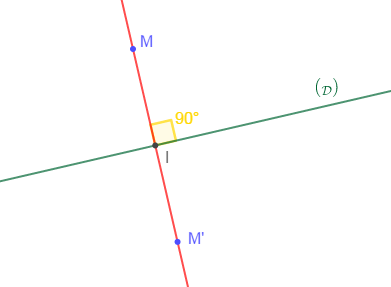
On dit que le point $M'$ est le symétrique de $M$ par rapport à la droite $(\mathcal{D}).$
On note :
$$s_{(\mathcal{D})}(M)=M'$$
I.5. Construction à la règle et au compas
Je trace la droite $(\mathcal{D})$ et je place le point $M.$
Avec un même écartement du compas, je place deux points $A\ $ et $\ B$ équidistants par rapport à $M$ sur la droite $(\mathcal{D}).$
Sans changer l'écartement du compas, je trace à partir de $A\ $ et $\ B$ deux arcs de cercle de l'autre coté de la droite.
Ces deux arcs se recoupent en un point ; c'est le point $M'$ symétrique de $M$ par rapport à $(\mathcal{D}).$
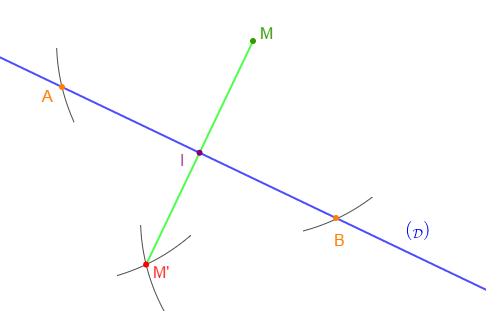
On note :
$$s_{(\mathcal{D})}(M)=M'$$
Remarque
Tout point $M$ appartenant à la droite $(\mathcal{D})$ est son propre symétrique.
On note :
$$s_{(\mathcal{D})}(M)=M$$
II. Symétrique d'une figure simple
II.1. Symétrique d'un segment
Trace un segment $[AB]$ et une droite $(L)$ hors de $[AB].$
Construire les points $A'\ $ et $\ B'$ symétriques respectifs de $A\ $ et $\ B$ par rapport à $(L).$
Quelle est le symétrique du segment $[AB]\ ?$
$$\left.\begin{array}{lll} s_{(L)}(A)&=&A'\\s_{(L)}(B)&=&B'\end{array}\right\rbrace\quad\text{donc, }\quad s_{(L)}([AB])=[A'B']$$
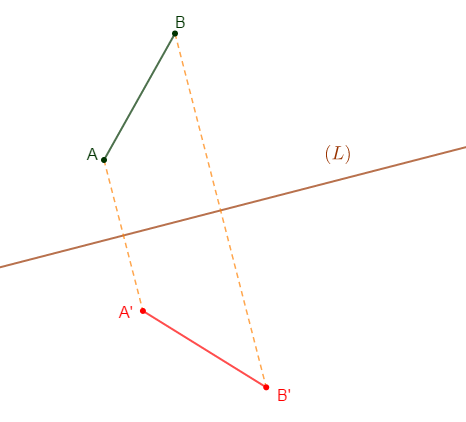
Le symétrique d'un segment $[AB]$ est le segment $[A'B'].$
D'une manière générale, le symétrique d'un segment par rapport à une droite est un segment de même longueur.
II.2. Symétrique d'une demi-droite
Trace une droite $(\Delta).$
Trace une demi-droite $[AB).$
Construis les points $A'\ $ et $\ B'$ symétriques respectifs de $A\ $ et $\ B$ par rapport à $(\Delta).$
$$\left.\begin{array}{lll} s_{(\Delta)}(A)&=&A'\\s_{(\Delta)}(B)&=&B'\end{array}\right\rbrace\quad\text{par suite, }\quad s_{(\Delta)}([AB))=[A'B')$$
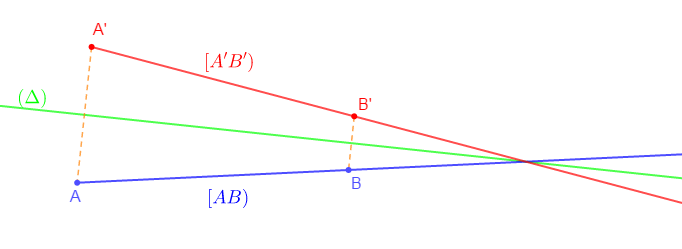
Le symétrique d'une demi-droite $[AB)$ est la demi-droite $[A'B').$
D'une manière générale, le symétrique d'une demi-droite par rapport à une droite est une demi-droite.
II.3. Symétrique d'une droite
Trace une droite $(D).$
Trace une droite $(L).$
Construis le symétrique $(L')$ de la droite $(L)$ par rapport à la droite $(D).$
Soient $A\ $ et $\ B$ deux points de $(L)$ et soient $A'\ $ et $\ B'$ leurs symétriques respectifs par rapport à $(D).$
Alors, $(L')$ passe par $A'\ $ et $\ B'.$ On a :
$$\left.\begin{array}{lll} s_{(D)}(A)&=&A'\\s_{(D)}(B)&=&B'\end{array}\right\rbrace\quad\text{donc, }\quad s_{(D)}((L))=(L')$$
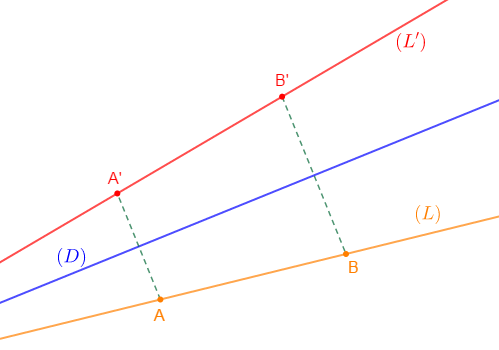
D'une manière générale, le symétrique d'une droite par rapport à une droite est une droite.
II.4. Symétrique d'un cercle
Soit un cercle $(\mathcal{C})$ de centre $O$ et de rayon $2\;cm.$
Trace une droite $(\Delta)$ et marque un point $A$ appartenant à $(\mathcal{C}).$
Construis les points $O'\ $ et $\ A'$ symétriques respectifs de $O\ $ et $\ A$ par rapport à la droite $(\Delta).$
Quelle est le symétrique du cercle $(\mathcal{C})\ ?$
$$\left.\begin{array}{lll} s_{(\Delta)}(O)&=&O'\\s_{(\Delta)}(A)&=&A' \end{array}\right\rbrace\quad\text{donc, }\quad s_{(\Delta)}([OA])=[O'A']$$
D'où,
$$s_{(\Delta)}(\mathcal{C}(O\;;\ OA))=\mathcal{C}'(O'\;;\ O'A')\quad\text{ avec, }OA=O'A'=2\;cm$$
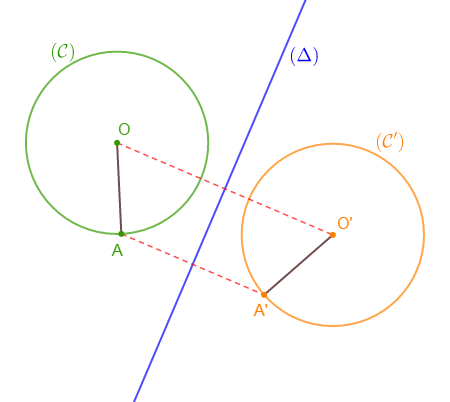
Le symétrique d'un cercle est un cercle de même rayon.
II.5. Symétrique d'un angle
On donne un angle $\widehat{(ABC)}.$
Trace une droite $(D).$
Construis les points $A'\;,\ B'\ $ et $\ C'$ symétriques respectifs de $A\;,\ B\ $ et $\ C$ par rapport à la droite $(D).$
Quelle est le symétrique de l'angle $\widehat{(ABC)}\ ?$
$$\left.\begin{array}{lll} s_{(D)}(A)&=&A'\\s_{(D)}(B)&=&B'\\s_{(D)}(C)&=&C'\end{array}\right\rbrace\quad\text{donc, }\quad s_{(D)}(\widehat{(ABC)})=\widehat{(A'B'C')}$$
De plus, $mes\,\widehat{(ABC)}=mes,\widehat{(A'B'C')}$
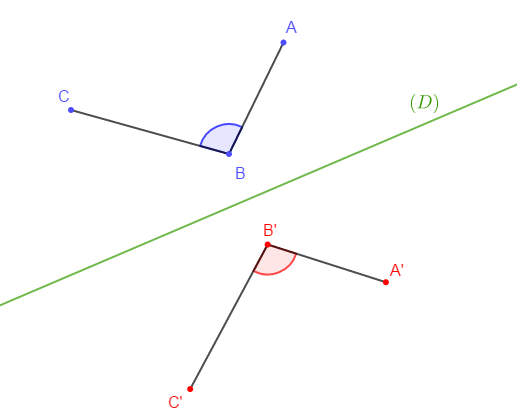
Le symétrique d'un angle est un angle de même mesure.
II.6. Symétrique d'un triangle
Construis un triangle $ABC.$
Trace une droite $(\Delta).$
Construis les points $A'\;,\ B'\ $ et $\ C'$ symétriques respectifs de $A\;,\ B\ $ et $\ C$ par rapport à la droite $(\Delta).$
Quelle est le symétrique du triangle $ABC$ par rapport à la droite $(\Delta)\ ?$
$$\left.\begin{array}{lll} s_{(\Delta)}(A)&=&A'\\s_{(\Delta)}(B)&=&B'\\ s_{(\Delta)}(C)&=&C'\end{array}\right\rbrace\quad\text{par suite, }\quad s_{(\Delta)}(ABC)=(A'B'C')$$
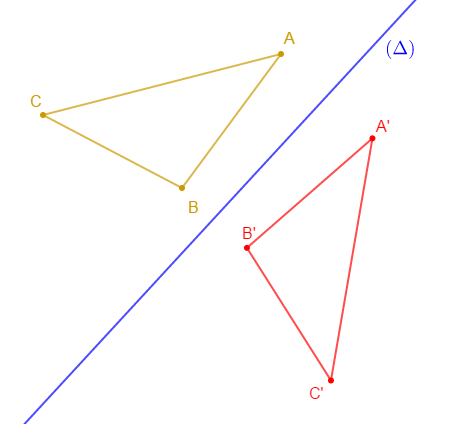
Le symétrique d'un triangle est un triangle de même nature.
II.7. Symétriques de droites parallèles
Soit $(D_{1})\ $ et $\ (D_{2})$ deux droites parallèles.
Trace une $(\Delta).$
Construis $(D_{1}')\ $ et $\ (D_{2}')$ symétriques respectifs des droites $(D_{1})\ $ et $\ (D_{2})$ par rapport à la droite $(\Delta).$
Comment sont les droites $(D_{1}')\ $ et $\ (D_{2}')\ ?$
$$\left.\begin{array}{lll} s_{(\Delta)}(D_{1})&=&(D_{1}')\\ s_{(\Delta)}(D_{2})&=&(D_{2}')\end{array}\right\rbrace\quad\text{par suite, }\quad s_{(\Delta)}((D_{1})\parallel(D_{2}))=(D'_{1})\parallel(D'_{2})$$
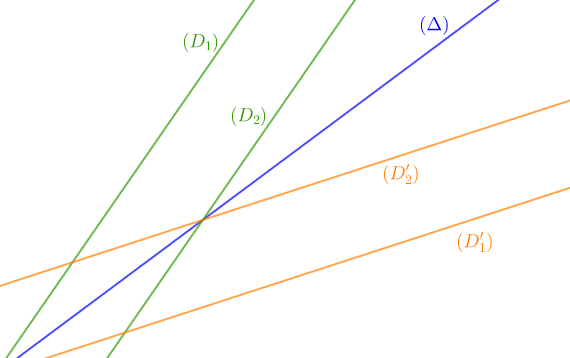
Les symétriques de deux droites parallèles sont deux droites parallèles.
II.8. Symétriques de droites perpendiculaires
$(D_{1})\ $ et $\ (D_{2})$ sont deux droites perpendiculaires.
Soit $(\Delta)$ une droite donnée.
Construis $(D_{1}')\ $ et $\ (D_{2}')$ symétriques respectifs des droites $(D_{1})\ $ et $\ (D_{2})$ par rapport à la droite $(\Delta).$
Comment sont les droites $(D_{1}')\ $ et $\ (D_{2}')\ ?$
$$\left.\begin{array}{lll} s_{(\Delta)}(D_{1})&=&D_{1}'\\s_{(\Delta)}(D_{2})&=& D_{2}'\end{array}\right\rbrace\quad\text{donc, }\quad s_{(\Delta)}((D_{1})\perp(D_{2}))=(D'_{1})\perp(D'_{2})$$
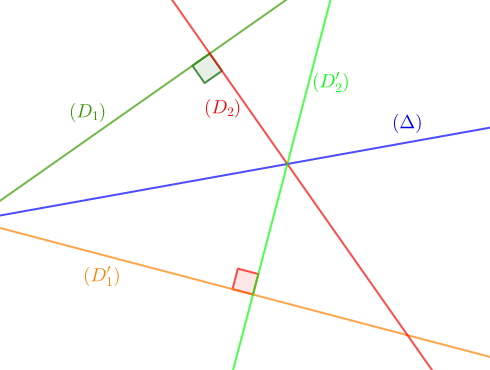
Les symétriques de deux droites perpendiculaires sont deux droites perpendiculaires.
III. Axes de symétrie
Une droite $(d)$ est un axe de symétrie d'une figure, si les deux parties de la figure se superposent par un pliage le long de la droite $(d)$
III.1. Axe de symétrie d'un segment
Trace un segment $[AB].$
Trace la droite $(d)$ médiatrice du segment $[AB].$
$(d)$ est un axe de symétrie de $[AB].$
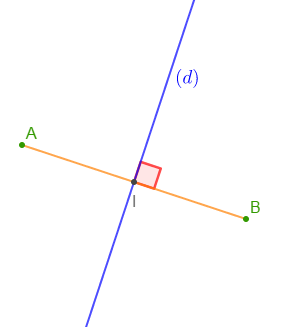
D'une manière générale l'axe de symétrie d'un segment est la médiatrice de ce segment.
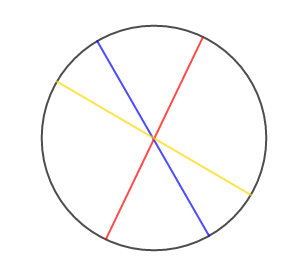
III.2. Axe de symétrie d'un cercle
Dans un cercle, tout diamètre est axe de symétrie de ce cercle
III.3. Axe de symétrie d'un triangle isocèle
Soit $ABC$ un triangle isocèle en $A.$
Construis la médiane issue de $A.$
Cette médiane est l'axe de symétrie du triangle isocèle.
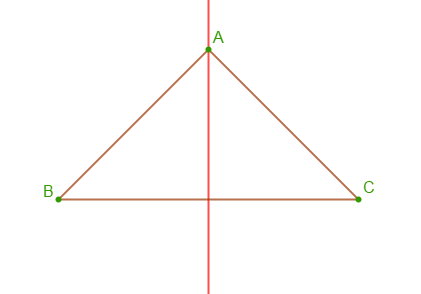
Dans un triangle isocèle, la médiane issue du sommet où le triangle est isocèle constitue l'axe de symétrie de ce triangle.
III.4. Axe de symétrie d'un triangle équilatéral
Soit $ABC$ un triangle équilatéral.
Trace toutes les médianes de ce triangle.
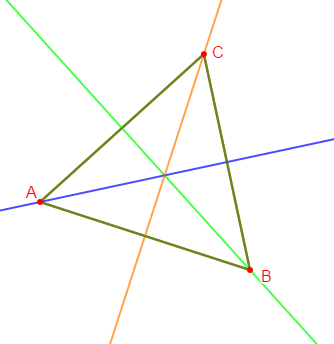
Pour un triangle équilatéral, chaque médiane est axe de symétrie.
Donc, dans un triangle équilatéral on distingue trois axes de symétrie.
IV. Propriétés
$\centerdot\ $ Conservation des distances : Pour un segment de longueur donnée, son image par symétrie orthogonale est un segment de même longueur.
$\centerdot\ $ Milieu d'un segment : L'image du milieu d'un segment par symétrie orthogonale est le milieu de l'image de ce segment.
$\centerdot\ $ Points alignés : Les images de points alignés par symétrie orthogonale sont encore des points alignés, dans le même ordre.
$\centerdot\ $ Droites perpendiculaires : Les images de droites perpendiculaires par symétrie orthogonale sont également des droites perpendiculaires.

Commentaires
Mame saye kane (non vérifié)
sam, 06/11/2022 - 21:30
Permalien
Pour être plus efficace et plus précis et plus fonctionnel, fort
Mame saye kane (non vérifié)
sam, 06/11/2022 - 21:30
Permalien
Pour être plus efficace et plus précis et plus fonctionnel, fort
Mame saye kane (non vérifié)
sam, 06/11/2022 - 21:30
Permalien
Pour être plus efficace et plus précis et plus fonctionnel, fort
Ajouter un commentaire