Bac Physique Chimie 1er Groupe S2 S2A S4 S5 2012
Exercice 1 (04 points)
Dans une fiole jaugée de $500\;mL$, on introduit un volume $V_{0}=20\;mL$ d'une solution $S_{0}$ d'un monoacide de concentration $C_{0}$ inconnue.
On complète jusqu'au trait de jauge avec de l'eau distillée.
On dose la solution S ainsi obtenue à l'aide d'une solution d'hydroxyde de sodium de concentration molaire $C_{b}=0.20\;mol\cdot L^{-1}.$
Le dosage suivi au $pH$-mètre a permis d'obtenir le tableau de valeurs suivant :
$$\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|} \hline V_{b}(mL)&2.0&4.0&6.0&8.0&9.0&9.9&10.1&11.0&12.0&14.0&16.0\\ \hline pH&2.2&2.6&2.8&3.1&3.4&4.4&9.6&10.6&10.9&11.2&11.4\\ \hline \end{array}$$
1.1 Faire le schéma annoté du dispositif de dosage. $(0.5\;pt)$
1.2 Tracer la courbe du $pH$ du milieu en fonction du volume $V_{b}$ d'hydroxyde de sodium versé (la courbe est à rendre avec la copie). $(01\;pt)$
1.3 Déterminer graphiquement les coordonnées du point d'équivalence.
L'acide dosé est-il un acide faible ?
Justifier. $(01\;pt)$
1.4 Déterminer la concentration $C_{0}$ de la solution $S_{0}.$ $(0.5\;pt)$
1.5 Au lieu de suivre le dosage au moyen d'un $pH$-mètre on utilise un indicateur coloré, l'hélianthine.
Le début du virage de l'indicateur se produit pour un $pH$ voisin de $3.3.$
Quelle erreur relative commet-on sur la concentration de $S_{0}$ si on arrête l'addition de la solution d'hydroxyde de sodium dès le début du virage de l'hélianthine ? $(0.5\;pt)$
1.6 Si on avait dosé $50\;mL$ de la solution $S$ avec la solution de soude à $0.20\;mol\cdot L^{-1}$ quel serait le volume équivalent ?
Commenter le résultat. $(0.5\;pt)$
Exercice 2 (04\;points)
Les acides $\alpha$ aminés jouent un rôle important dans la vie, en particulier en biochimie.
Ce sont les éléments constitutifs des protéines.
2.1 L'acide $\alpha$ aminé $A$, de formule semi-développée $CH_{3}-CH\left(CH_{3}\right)-CH\left(NH_{2}\right)-CO_{2}H$ fait partie des vingt principaux acides $\alpha$ aminés des organismes vivants.
2.1.1 Donner, dans la nomenclature officielle, le nom de l'acide $\alpha$ aminé $A.$ $(0.25\;pt)$
2.1.2 Donner la représentation de Fischer des deux énantiomères de cet acide $\alpha$ aminé. $(0.25\;pt)$
2.2 On réalise la réaction de condensation d'un acide $\alpha$ aminé $B$ de formule semi-développée
$R-CH\left(NH_{2})-CO_{2}\right)H$ sur l'acide $\alpha$ aminé $A$ ($R$ est un radical alkyl ou un atome d'hydrogène).
On ne tiendra pas compte, dans cette question, de l'isomérie optique et on ne considèrera que les réactions possibles entre $A$ et $B.$
2.2.1 Combien de dipeptides peut-on alors obtenir ?
Écrire les équations des réactions mises en jeu $(0.75\;pt)$
2.2.2 Encadrer la liaison peptidique pour chaque dipeptide obtenu. $(0.5\;pt)$
2.2.3 Sachant que chaque dipeptide a une masse molaire $M=174\;g\cdot mol^{-1}$, déterminer la formule semi-développée et le nom de l'acide $\alpha$ aminé $B.$ $(0.75\;pt)$
2.3 L'acide $\alpha$ aminé $B$ ressemble beaucoup, quand il est pur, à un corps à structure ionique.
Il se présente en effet sous la forme d'un ion bipolaire (amphion ou zwitterion).
2.3.1 Écrire la formule semi développée de cet ion bipolaire. $(0.25\;pt)$
2.3.2 Justifier son caractère amphotère. $(0.25\;pt)$
2.3.3 En déduire les couples acide/base qui lui sont associés. $(0.5\;pt)$
2.3.4 Les $pKa$ de ces couples acide/base ont pour valeur $pKa_{1}=2.3$ et $pKa_{2}=9.8.$
a) Associer à chaque couple acide/base un $pKa.$ $(0.25\;pt)$
b) Compléter le diagramme ci-dessous en y indiquant les espèces acido-basiques majoritaires de l'acide $\alpha$ aminé $B$ pour chaque domaine de $pH.$ $(0.25\;pt)$

Exercice 3 (04 points)
Lors des derniers championnats du monde d'athlétisme qui eurent lieu à Paris en août $2003$, le vainqueur de l'épreuve du lancer de poids a réussi un jet à une distance $D=21.69 \;m.$
L'entraîneur de l'un de ses concurrents souhaite étudier ce lancer.
Il cherche à déterminer les conditions initiales avec lesquelles cette performance a pu être réalisée par le vainqueur de l'épreuve.
Il dispose pour cela d'enregistrements relatifs à la vitesse du boulet (nom donné au « poids »).
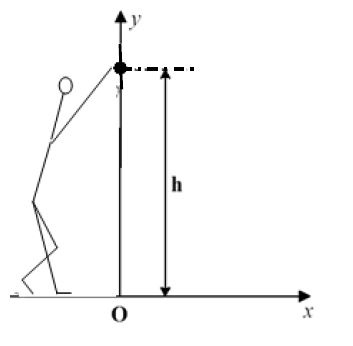
Pour simplifier, l'étude porte sur le mouvement du centre d'inertie du boulet dans le référentiel terrestre où on définit le repère d'espace $(O\;,\ \vec{x}\;,\ \vec{y})$ où :
$\bullet$ $Oy$ est un axe vertical ascendant passant par le centre d'inertie du boulet à l'instant où il quitte la main du lanceur.
$\bullet$ $Ox$ est un axe horizontal au niveau du sol.
L'origine des temps $t=0$ est prise au moment du lancer du boulet où son centre d'inertie est situé à la distance verticale $h=2.62\;m$ du sol.
3.1 Exploitation des enregistrements.
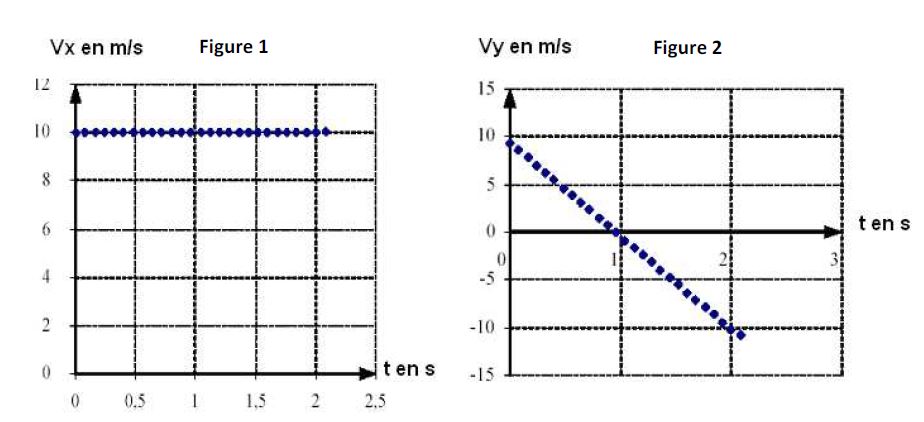
L'entraineur a obtenu les graphes, en fonction du temps, des composantes horizontale $v_{x}$ et verticale $v_{y}$ du vecteur-vitesse instantanée (figures 1 et 2 ci-dessous).
Pour chacun des graphes, les dates correspondant à deux points successifs sont séparées par le même intervalle de temps.
NB :
Ces courbes ne sont pas à rendre avec la copie.
On expliquera simplement l'exploitation qui en est faite pour répondre aux questions.
3.1.1 En utilisant la figure 1, déterminer :
a) la composante $v_{Ox}$ du vecteur-vitesse du centre d'inertie du boulet à l'instant de date $t=0s.$ $(0.25\;pt)$
b) la nature du mouvement de la projection du centre d'inertie du boulet sur l'axe $Ox.$ $(0.25\;pt)$
3.1.2 En utilisant la figure 2, déterminer :
a) la composante $v_{Oy}$ du vecteur-vitesse à l'instant de date $t=0\;s.$ $(0.25\;pt)$
b) la nature du mouvement de la projection du centre d'inertie du boulet sur l'axe $OY.$ $(0.25\;pt)$
3.1.3 Exprimer les composantes $v_{Ox}$ et $v_{Oy}$ en fonction de la valeur $V_{0}$ du vecteur-vitesse initiale et de l'angle $\alpha$ de ce vecteur avec l'horizontale. $(0.5\;pt)$
3.1.4 En déduire la valeur de $V_{0}$ et celle de l'angle $\alpha.$ $(01\;pt)$
3.2 Étude théorique du mouvement.
3.2.1 Par application du théorème du centre d'inertie, dans le référentiel terrestre supposé galiléen, déterminer le vecteur-accélération du centre d'inertie du boulet lors du mouvement. $(0.25\;pt)$
3.2.2 En déduire les équations, en fonction du temps, des composantes $V_{x}$ et $V_{y}$ du vecteur-vitesse instantanée $\overrightarrow{V}$.
Ces équations sont-elles en accord avec les graphes des figures 1 et 2 ? $(0.5\;pt)$
3.2.3 Établir les équations horaires $x(t)$ et $y(t)$ du mouvement.
En déduire l'équation de la trajectoire.
Représenter cette trajectoire et le vecteur-vitesse $\overrightarrow{V_{0}}$ au point de départ du boulet. $(0.75\;pt)$
On prendra : $g=9.8\;m\cdot s^{-2}$
Exercice 4 (04 points)
Les bobines sont des composants électriques de très grande utilité sur lesquels le fabricant mentionne les caractéristiques ($L$, $N$, $I_{max}$), pour une utilisation optimale et sécuritaire.
$L$ et $N$ représentent respectivement l'inductance et le nombre de spires de la bobine tandis que $I_{max}$ correspond à l'intensité maximale du courant électrique qui peut traverser la bobine.
4.1 Un groupe d'élèves, sous la supervision de leur professeur, se propose de vérifier quelques caractéristiques d'une bobine de leur laboratoire.
Cette bobine est assimilée à un solénoïde de longueur $\ell=0.5\;m$, comportant $N$ spires de rayon $R=5\;cm.$
Pour ce faire, ils disposent la bobine horizontalement, son axe $(\Delta)$ étant orthogonal au plan méridien magnétique.
Au centre de cette bobine est placée une petite aiguille aimantée horizontale mobile autour d'un axe vertical $(\Delta').$
Le groupe d'élèves lance un courant électrique d'intensité $I$ dans le solénoïde et constate que l'aiguille dévie d'un angle $\alpha.$
4.1.1 Faire un schéma où seront représentés la bobine en indiquant le sens du courant, le vecteur champ magnétique $\overrightarrow{B_{C}}$ créé par le courant, le vecteur $\overrightarrow{B_{H}}$ composante horizontale du champ magnétique terrestre, la position finale de l'aiguille et l'angle $\alpha.$ $(0.75\;pt)$
4.1.2 Exprimer $\tan\alpha$ en fonction de $B_{H}$, $N$, $l$ , $\ell$ et $\mu_{0}$ (perméabilité magnétique du vide) $(0.5\;pt)$
4.2 Le groupe fait varier l'intensité $I$ du courant dans le circuit et mesure la valeur de l'angle $\alpha$ pour chaque valeur de $I.$
Les résultats obtenus permettent de tracer la courbe $\tan\alpha=f(I).$ (figure 1)
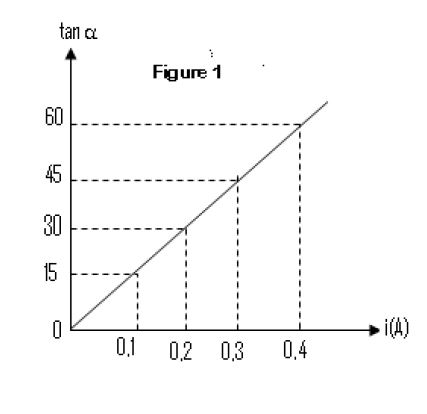
4.2.1 Déterminer à partir de cette courbe la relation entre $\tan\alpha$ et $I$
NB :
Il n'est pas demandé de rendre la courbe avec la copie. $(0.5\;pt)$
4.2.2 En déduire la valeur de $N$ que l'on notera $N_{0}.$ $(0.25\;pt)$
On donne :
$\mu_{0}=4\pi 10^{-7}\;SI$ ;
$B_{H}=2\cdot10^{-5}T$
4.2.3 Déterminer l'inductance $L$ du solénoïde (on prendra $N=1195$ spires). $(0.75\;pt)$
4.3 Afin d'étudier le comportement de la bobine dans un circuit, les élèves réalisent avec ce solénoïde le montage ci-après (figure 2).
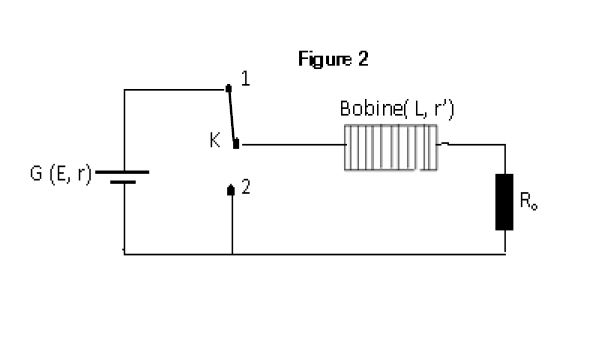
La bobine est branchée en série avec un résistor de résistance $R_{0}=10\Omega.$
Ils utilisent un générateur de courant continu $G$ ($E=12V$ ; $r=5\Omega$).
La résistance interne du solénoïde est $r'=5\Omega.$
Le nombre de spires est $N=1195$ spires.
L'interrupteur est dans la position $1.$
4.3.1 Déterminer l'intensité $I_{0}$ du courant dans le circuit en régime permanent. $(0.25\;pt)$
4.3.2 En un temps très bref et à $t=0$, on bascule l'interrupteur de la position $(1)$ à la position $(2).$
a) Établir l'équation différentielle à laquelle obéit l'intensité $i$ du courant dans le circuit. $(0.5\;pt)$
b) Vérifier que $i=A\mathrm{e^{-\dfrac{t}{\tau}}}$ est solution de cette équation différentielle, $A$ et $\tau$ étant des constantes à exprimer en fonction des caractéristiques des composants du circuit.
Donner l'allure de la courbe $i=f(t).$ $(0.5\;pt)$
Exercice 5 (04 points)
Actuellement des techniques telles que la scintigraphie sont utilisées en médecine grâce à des substances radioactives comme le technétium.
Le technétium, se fixant préférentiellement sur les lésions osseuses du squelette, peut être détecté par une gamma-caméra.
Ce dernier fournit par la suite une image du squelette appelée scintigraphie osseuse.
Tous les noyaux du technétium sont radioactifs.
5.1 L'isotope $97$ du technétium $_{43}^{97}Tc$ , de demi-vie $90.1$ jours, est synthétisé en bombardant un noyau de molybdène $96$, $^{96}_{42}Mo$ avec un noyau de deutérium $_{Z}^{A}X.$
5.1.1 Qu'appelle-t-on noyaux isotopes ? $(0\;25\;pt)$
5.1.2 Écrire l'équation de la réaction de synthèse du technétium $_{43}^{97}Tc$ à partir du molybdène $^{96}_{42}Mo$ en précisant les valeurs de $A$ et $Z$ sachant qu'il se forme en même temps un neutron.
A quel élément chimique appartient le deutérium ? $(0.75\;pt)$
5.2 L'isotope $99$ du technétium $_{43}^{99}Tc$ présente la particularité et l'avantage de pouvoir être produit sur place par désintégration du molybdène $99$, $^{99}_{42}Mo.$
Une infirmière prépare une dose de technétium $99$, $_{43}^{99}Tc.$
Deux heures après, son activité étant égale à $79.5\%$ de sa valeur initiale, elle l'injecte à un patient.
5.2.1 Écrire l'équation de la réaction nucléaire permettant d'obtenir le technétium $99$ à partir du molybdène $99.$
Préciser le type de désintégration dont il s'agit. $(0.5\;pt)$
5.2.2 Définir l'activité d'une source radioactive et établir la relation entre l'activité, la constante radioactive et le nombre de noyaux présents. $(0.5\;pt)$
5.2.3 Déterminer la valeur de la période radioactive du technétium $99.$ $(0.75\;pt)$
5.2.4 L'activité maximale des doses administrées en $_{43}^{99}Tc$ ne doit pas dépasser $10^{9}Bq.$
Quelle est la masse maximale de technétium $99$ que doit contenir la dose préparée ? $(0.75\;pt)$
5.3 Le médecin porte son choix sur le produit qui disparait le plus vite.
Lequel des deux isotopes du technétium va-t-il choisir ?
Justifier la réponse. $(0.5\;pt)$
Données :
$1u=931.5\;MeV/c^{2}=1.66\cdot10^{-27} kg.$
$$\begin{array}{|c|c|c|c|c|} \hline \text{Particule ou noyau}&^{60}_{27}Co&_{28}^{60}Ni&\text{électron}&_{43}^{99}Tc\\ \hline \text{Masse en }u&59.934&59.931&5.486\cdot10^{-4}&98.882\\ \hline \end{array}$$

Commentaires
Djibson (non vérifié)
ven, 05/01/2020 - 06:47
Permalien
épreuve corrigé du bac 2012maths
Anonyme (non vérifié)
mar, 06/28/2022 - 10:57
Permalien
C très bonne pour les eleves
Ajouter un commentaire