Solutions des exercices : Étude du Dipôle RC - Ts
Classe:
Terminale
Exercice 1
1) Schéma du montage ;
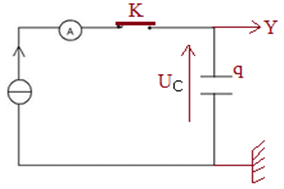
2) Établissement de la relation entre $I$, $C$, $U_{C}$ et $t.$
$U_{C}=\dfrac{q}{C}\text{ or }q=It\Rightarrow\,U_{C}\dfrac{I}{C}t$
3) Détermination de la valeur de la capacité $C$ du condensateur
La courbe représentant la tension $U_{C}$ aux du condensateur en fonction du temps $t$ est une droite qui passe par l'origine de coefficient directeur $\dfrac{I}{C}$
$\begin{array}{rcl} \dfrac{I}{C}&=&\dfrac{\Delta U_{C}}{\Delta t}\\\\\Rightarrow\,C&=&I\dfrac{\Delta t}{\Delta U_{C}}\\\\&=&0.5\cdot 10^{-3}\times\dfrac{15-0}{3.5-0}\\\\\Rightarrow\,C&=&2.1\cdot 10^{-3}F \end{array}$
4) a) Calcul de la tension de claquage du condensateur.
$\begin{array}{rcl} U_{C}&=&\dfrac{I}{C}t_{\text{max}}\\\\&=&0.5\cdot 10^{-3}\times\dfrac{2\times 60}{2.1\cdot 10^{-3}}\\\\\Rightarrow\,U_{C}&=&28.6V \end{array}$
b) L'énergie électrique maximale emmagasinée par le condensateur
$\begin{array}{rcl} E_{\text{max}}&=&\dfrac{1}{2}CU_{C}^{2}\\\\&=&\dfrac{1}{2}\times 2.1\cdot 10^{-3}\times(28.6)^{2}\\\\\Rightarrow\,E_{\text{max}}&=&0.86J \end{array}$
Exercice 2
1) a) L'interrupteur en position $1$ correspond à la charge du condensateur ; en position $2$ correspond à la décharge du condensateur
1) b) La fig2 correspond la charge du condensateur, car la charge d'un condensateur est proportionnelle à l'intensité du courant délivré par le générateur de courant.
2) a) Calcul de la charge du condensateur à la date $40s.$
$\begin{array}{rcl} Q&=&It\\\\&=&10^{-6}\times 40\\\\\Rightarrow\,Q&=&40\cdot 10^{-6}C \end{array}$
2) b) Valeur de l'énergie emmagasinée par le condensateur à la date $40s$
$\begin{array}{rcl} E&=&\dfrac{1}{2}QU_{C}\\\\&=&\dfrac{1}{2}\times 40\cdot 10^{-6}\times 40\\\\\Rightarrow\,E&=&80\cdot 10^{-3}J \end{array}$
2) c) La capacité du condensateur
$\begin{array}{rcl} E&=&\dfrac{1}{2}CU_{C}^{2}\\\\\Rightarrow\,C&=&\dfrac{2E}{U_{C}^{2}}\\\\&=&\dfrac{2\times 80\cdot 10^{-3}}{40^{2}}\\\\\Rightarrow\,C&=&10\cdot 10^{-3}F \end{array}$
3. a. Détermination de la permittivité électrique absolue $\varepsilon$ du diélectrique de ce condensateur.
$\begin{array}{rcl} C&=&\dfrac{\varepsilon S}{e}\\\\\Rightarrow\varepsilon&=&\dfrac{e\times C}{S}\\\\&=&\dfrac{0.02\cdot 10^{-3}\times 10\cdot 10^{-3}}{0.1}\\\\\Rightarrow\varepsilon&=&2\cdot 10^{-8}(S.I) \end{array}$
b) $\begin{array}{rcl} \varepsilon_{r}&=&\dfrac{\varepsilon}{\varepsilon_{0}}\\\\&=&\dfrac{2\cdot 10^{-8}}{8.85\cdot 10^{-12}}\\\\\Rightarrow\varepsilon_{r}&=&2.3\cdot 10^{3} \end{array}$
Exercice 3
1) a) Précisons le graphe correspondant à la charge $q=f(t)$ et celui correspondant à la tension $u_{R1}=g(t).$
Lorsque le condensateur est chargé, l'intensité du courant de charge est nulle. En conséquence, le graphe représentant la charge est croissant ; tandis que celui représentant le courant décroissant.
Le graphe de la fig3 représente la charge $q=f(t)$ et la fig4 celui de la tension $u_{R1}=g(t)$ image du courant.
b) Établissement de la relation entre $q$, $u_{R1}$, $E$ et $C$
La loi d'additivité des tensions s'écrit :
$\begin{array}{rcl} u_{C}+u_{R1}&=&E\\\\\text{or }u_{C}&=&\dfrac{q}{C}\\\\\Rightarrow\dfrac{q}{C}+u_{R1}&=&E\\\\\Rightarrow\,u_{R1}&=&E-\dfrac{q}{C} \end{array}$
c) Montrons qu'à la date $t=0$, la tension $u_{R1}$ est égale à $E.$
$\begin{array}{rcl} u_{R1}&=&E-\dfrac{q}{C}\\\\\text{or }t=0\ ;\ q=0\\\\\Rightarrow\,u_{R1}&=&E \end{array}$
Valeur de $u_{R1}$
$u_{R1}=2\times 5=10V$
d) Valeur de la charge électrique maximale $Q_{\text{max}}$ du condensateur
$\begin{array}{rcl} Q_{\text{max}}&=&5\times 2\cdot 10^{-4}\\\\&=&10^{-3}C \end{array}$
2) a) Définition la constante de temps $\tau$ d'un dipôle $RC$
La constante de temps $\tau$ correspond au temps de charge ou de décharge d'un condensateur et est égal : $\tau=RC$
Montrons que $\tau$ est un temps
$\begin{array}{rcl} \tau&=&R\times C\\\\&=&\dfrac{U}{I}\times\dfrac{Q}{U}\\\\&=&\dfrac{Q}{I}\\\\&=&\dfrac{It}{I}\\\\&=&t \end{array}$
b) Montrons que l'équation différentielle régissant les variations de $u_{R1}$ au cours du temps peut s'écrire sous la forme
$$\tau_{1}\dfrac{\mathrm{d}u_{R1}}{\mathrm{d}t}+u_{R1}=0$$
La loi d'additivité des tensions s'écrit :
$u_{C}+u_{R1}=E$
or $u_{C}=\dfrac{q}{C}$
et $u_{R1}=R_{1}i\Rightarrow\,i=\dfrac{u_{R1}}{R_{1}}$
$\begin{array}{rcl} \dfrac{\mathrm{d}}{\mathrm{d}t}\left(\dfrac{q}{C}+u_{R1}\right)&=&\dfrac{\mathrm{d}}{\mathrm{d}t}E\\\\\Rightarrow\dfrac{1}{C}\dfrac{\mathrm{d}q}{\mathrm{d}t}&=&0\\\\\Rightarrow\dfrac{1} {C}i+\dfrac{\mathrm{d}u_{R1}}{\mathrm{d}t}&=0\\\\\Rightarrow\dfrac{u_{R_{1}}}{R_{1}C}+\dfrac{\mathrm{d}u_{R1}}{\mathrm{d}t}&=&0\\\\\Rightarrow\,R_{1}C\dfrac{\mathrm{d}u_{R1}}{\mathrm{d}t}+u_{R1}&=&0\\\\\Rightarrow\tau_{1}\dfrac{\mathrm{d}u_{R1}}{\mathrm{d}t}+u_{R1}&=&0\ ;\\\\\text{avec }\tau_{1}&=&R_{1}C \end{array}$
c) Détermination de $A$ et $\alpha.$
$u_{R1}=Ae^{-\alpha t}$ ;
$\tau_{1}\dfrac{\mathrm{d}u_{R1}}{\mathrm{d}t}+u_{R1}=0$

Commentaires
Anonyme (non vérifié)
sam, 07/09/2022 - 13:24
Permalien
D’où viens la relation R = u
Camila (non vérifié)
mar, 12/05/2023 - 20:39
Permalien
Demande
Anonyme (non vérifié)
jeu, 01/18/2024 - 18:22
Permalien
Erreur
Ajouter un commentaire