Équations et inéquations du 1er degré à deux inconnues 3e
Classe:
Troisième
I. Équations
Il s'agit des équations du type $ax+by+c=0$ où $a\;,\ b$ et $c$ sont des nombres réels $x$ et $y$ les inconnues à déterminer. La résolution de ce type d'équation revient tout simplement à exprimer l'une des inconnues en fonction de l'autre (plus précisément $y$ en fonction de $x$) à partir de l'équation donnée et représenter l'ensemble des solutions sous forme de couples $(x\;,\ y)$ liés par la relation antérieure.
La représentation graphique de l'ensemble des solutions est une droite dont l'expression réduite est la relation liant $y$ à $x.$
Exemple :
Résolvons et donnons la représentation graphique de l'équation $3x-y-5=0.$
On aura : $y=3x-5$
Alors, $$S=\{(x\;;\ y)\;\text{ tels que }\;y=3x-5\}$$
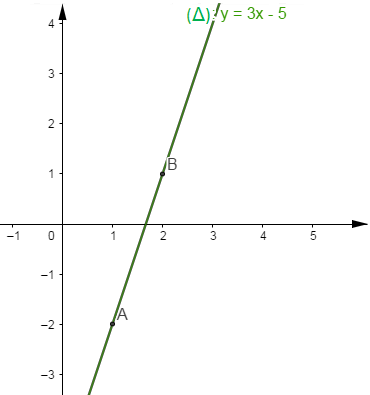
La représentation graphique de l'ensemble des solutions est la droite $(\Delta)\;:\ y=3x-5$
$\begin{array}{|c|c|c|}\hline & A & B \\ \hline x & 1 & 2 \\ \hline y & -2 & 1 \\ \hline\end{array}$
II. Inéquations
Il s'agit des inéquations du type $ax+by+c\leq 0$ où $a\;,\ b$ et $c$ sont des réels donnés, $x$ et $y$ les inconnues à déterminer.
La résolution de ce type d'inéquation s'appuie sur une interprétation graphique qui consiste tout d'abord à donner la représentation graphique de la droite $(\Delta)\;:\ ax+by+c=0$ puis, de déterminer le demi-plan solution obtenu à partir de la droite $(\Delta).$
Exemple 1 :
Résolvons l'inéquation $2x-3y+6\leq 0$
Soit $(\Delta)\;:\ 2x-3y+6=0$.
$\begin{array}{|c|c|c|}\hline & A & B \\ \hline x & 0 & -3 \\ \hline y & 2 & 0 \\ \hline\end{array}$
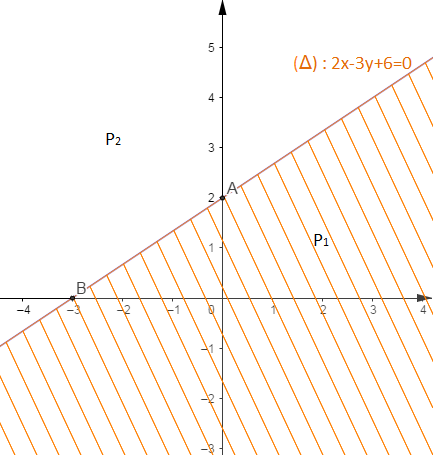
On prend $O\begin{pmatrix} 0\\ 0 \end{pmatrix}$ comme point de vérification.
Pour $2x-3y+6\leq 0$, on aura $2(0)-3(0)+6\leq 0$.
Alors, $0-0+6\leq 0$, donc $6\leq 0$ ; ce qui est impossible.
Ainsi, $P_{1}$ n'est pas solution de l'inéquation d'où, la partie non hachurée, $P_{2}$ est la solution graphique de l'inéquation $2x-3y+6\leq 0.$
Exemple 2 :
Résolvons l'inéquation $3x-2y\geq 0$
Soit $(\Delta)\;:\ 3x-2y=0$.
$\begin{array}{|c|c|c|}\hline & O & A \\ \hline x & 0 & 2 \\ \hline y & 0 & 3 \\ \hline\end{array}$
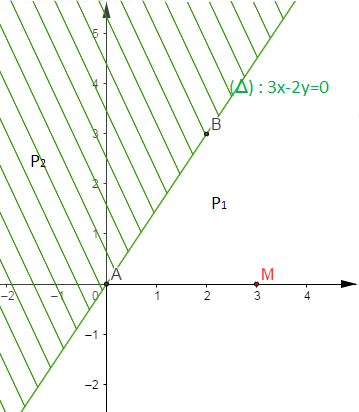
On prend $M\begin{pmatrix} 3\\ 0 \end{pmatrix}$ comme point de vérification.
Pour $3x-2y\geq 0$, on aura $3(3)-2(0)\geq 0$.
Alors, $9-0\geq 0$, donc $9\geq 0$ ; ce qui est toujours vraie.
Ainsi, $P_{1}$ est solution de l'inéquation d'où, la partie non hachurée, $P_{1}$ est la solution graphique de l'inéquation $3x-2y\geq 0.$
III. Système d'équations et d'inéquations
III.1 Système d'équations du 1er degré à deux inconnues
Il s'agit des systèmes du type $$\left\lbrace\begin{array}{lcl} ax+by &=& c\\ a'x+b'y &=& c' \end{array}\right.\quad \text{où } \ a, \ b,\ c,\ a',\ b'\ \text{ et } c'\ \in\mathbb{R}$$
$x$ et $y$ les inconnues à déterminer.
La résolution de ce type de système d'équations nous permet de solutionner les équations du problème, de trouver les points d'intersection de deux droites et de déterminer une application affine ou une équation de droite.
La résolution de ce type de système s'appuie sur trois méthodes de résolution ponctuées d'une méthode graphique.
III.1.1 Méthode de substitution
La méthode de substitution consiste à exprimer l'une des inconnues en fonction de l'autre dans l'une des deux équations et de la remplacer dans l'autre afin d'obtenir une équation du 1er degré à une inconnue.
Exemple :
Tante Adja dit à sa fille : "avec $6250\;F\;CFA$ j'achetais $10\;kg$ de pomme de terre et $20\;kg$ d'oignon mais après la dévaluation du $F\;CFA$ je dois payer $7950\;F\;CFA$ pour avoir les mêmes quantités".
Trouver le prix d'un $kg$ de pomme de terre et celui d'oignon avant la dévaluation sachant que ces prix ont été multipliés respectivement par $1.2$ et $1.3$ après la dévaluation.
Soit $x$ le prix d'un $kg$ de pomme de terre et $y$ celui d'oignon avant la dévaluation.
On aura : $10x+20y=6250$
Alors, $x+2y=625\quad (1)$
de plus on a $10(1.2x)+20(1.3y)=7950$
alors $12x+26y=7950$, donc $6x+13y=3975\quad (2)$
Ainsi, $$\left\lbrace\begin{array}{lcl} x+2y &=& 625\\ 6x+13y &=& 3975 \end{array}\right.$$
par suite $$\left\lbrace\begin{array}{lcl} x &=& 625-2y \\ 6(625-2y)+13y &=& 3975 \end{array}\right.$$
par conséquent $$\left\lbrace\begin{array}{lcl} x &=& 625-2y \\ 3750-12y+13y &=& 3975 \end{array}\right.$$
d'où, $$\left\lbrace\begin{array}{lcl} x &=& 625-2(225)= 625-450 = 175 \\ y &=& 3975-3750 = 225 \end{array}\right.$$
Le prix d'un $kg$ de pomme de terre avant la dévaluation était de $175\;F\;CFA$ et celui de l'oignon $225\;F\;CFA.$
III.1.2 Méthode de comparaison
Cette méthode consiste à exprimer l'une des inconnues en fonction de l'autre dans les deux équations puis de comparer les deux égalités obtenues.
Exemple :
Soit la droite $(D)\;:\ 2x+3y-8=0$ et $(\Delta)\;:\ -3x+4y-5=0$ et $A$ leur point d'intersection.
Trouvons les coordonnées du point $A$.
On a $A=(D)\cap(\Delta)$
Alors, $$\left\lbrace\begin{array}{lcl} 2x+3y-8 &=& 0 \qquad (1)\\ -3x+4y-5 &=& 0 \qquad (2) \end{array}\right.$$
donc $$\left\lbrace\begin{array}{lcl} y &=& \dfrac{-2x+8}{3}\\ \\ y &=& \dfrac{3x+5}{4} \end{array}\right.$$
Ainsi, $\dfrac{-2x+8}{3}=\dfrac{3x+5}{4}$
par suite $-8x+32=9x+15$
par conséquent $-17x=-17$ c'est à dire $x=1$.
En remplaçant $x=1$ dans $y=\dfrac{-2x+8}{3}$ on obtient $y=\dfrac{-2(1)+8}{3}=2$
d'où, $A\begin{pmatrix} 1\\ 2 \end{pmatrix} $
III.1.3 Méthode d'addition
La méthode d'addition consiste à trouver éventuellement des coefficients (à l'aide du calcul de PPMC des réels placés devant $x$ ou $y$) par lesquels il faudra les multiplier par les équations afin que la somme membre à membre des deux équations aboutisse à une équation du 1er degré à une seule inconnue.
Exemple :
Résolvons le système d'équations $$\left\lbrace\begin{array}{lcl} 2x+3y-8 &=& 0 \qquad (1)\\ -3x+4y-5 &=& 0 \qquad (2) \end{array}\right.$$
En multipliant donc (1) par 3 et (2) par 2 on aura $$\left\lbrace\begin{array}{lcl} 6x+9y-24 &=& 0 \\ -6x+8y-10 &=& 0 \end{array}\right.$$
Alors, $0+17y-34=0$ donc, $y=\dfrac{34}{17}=2$
En remplaçant $y=2$ dans l'équation (1), on obtient : $2x+3(2)-8=0.$
Ainsi, $2x-2=0$
par suite $x=1$; d'où $S=\{(1\;;\ 2)\}$
Remarque : cas des systèmes à trois équations
Exemple :
Résolvons le système d'équations suivant et donnons sa solution graphique.
$$\left\lbrace\begin{array}{lcl} x-y-1 &=& 0 \qquad (1)\\ 2x-y+2 &=& 0 \qquad (2)\\ -x+3y+9 &=& 0 \qquad (3) \end{array}\right.$$
La résolution de ce type de système d'équations revient tout simplement à résoudre un système composé par deux de ces trois équations puis de procéder à une vérification au niveau de la troisième équation non choisie.
On a : $$\left\lbrace\begin{array}{lcl} x-y-1 &=& 0 \qquad (1)\\ 2x-y+2 &=& 0 \qquad (2) \end{array}\right.$$
En multipliant donc (1) par -1 et (2) par 1 on aura $$\left\lbrace\begin{array}{lcl} -x+y+1 &=& 0 \\ 2x-y+2 &=& 0 \end{array}\right.$$
donc, par addition on obtient $x+0+3=0$. Ce qui donne $x=-3.$
En remplaçant $x=-3$ dans l'équation (1) on obtient $(-3)-y-1=0$ ; c'est à dire $y=-4.$
On vérifie si le couple $(-3\;;\ -4)$ est solution de l'équation (3).
On a $-(-3)+3(-4)+9=0$ c'est à dire $3-12+9=0$ ce qui est toujours vraie. Donc le couple $(-3\;;\ -4)$ vérifie bien l'équation (3).
D'où $S=\{(-3\;;\ -4)\}$
La résolution graphique d'un système d'équations revient tout simplement à traduire toute équation du système comme étant une équation de droite à représenter dans un repère dont leur point d'intersection est la solution graphique du système donné.
On a : $$\left\lbrace\begin{array}{lcl} x-y-1 &=& 0 \qquad (1)\\ 2x-y+2 &=& 0 \qquad (2)\\ -x+3y+9 &=& 0 \qquad (3) \end{array}\right.$$
Soient $(\Delta_{1})\;:\ x-y-1=0\;,\ (\Delta_{2})\;:\ 2x-y+2=0$ et $(\Delta_{3})\;:\ -x+3y+9=0$
$\begin{array}{|c|c|c|}\hline & A & B \\ \hline x & 0 & 1 \\ \hline y & -1 & 0 \\ \hline\end{array}\qquad\qquad \begin{array}{|c|c|c|} \hline & C & E \\ \hline x & 0 & -1 \\ \hline y & 2 & 0 \\ \hline\end{array}\qquad\qquad \begin{array}{|c|c|c|} \hline & F & G \\ \hline x & 0 & 3 \\ \hline y & -3 & -2 \\ \hline \end{array}$
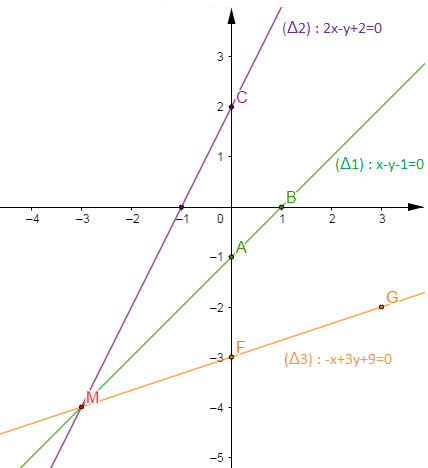
Le point $M\begin{pmatrix} -3 \\ -4 \end{pmatrix}$ est la solution graphique du système.
III.2 Système d'inéquations
Exemple :
Résolvons le système d'inéquations suivant $$\left\lbrace\begin{array}{lcl} 2x-3y &\geq & 0 \qquad (1)\\ x+2y-4 &\leq & 0 \qquad (2)\\ y+2 &\geq & 0 \qquad (3)\end{array}\right.$$
Soient $(\Delta_{1})\;:\ 2x-3y=0\;,\ (\Delta_{2})\;:\ x+2y-4=0$ et $(\Delta_{3})\;:\ y+2=0$
$\begin{array}{|c|c|c|}\hline & O & B \\ \hline x & 0 & 3 \\ \hline y & 0 & 2 \\ \hline\end{array}\qquad\qquad \begin{array}{|c|c|c|} \hline & C & E \\ \hline x & 0 & 4 \\ \hline y & 2 & 0 \\ \hline\end{array}\qquad\qquad \begin{array}{|c|c|c|}\hline & F & G \\ \hline x & 0 & 2 \\ \hline y & -2 & -2 \\ \hline\end{array}$
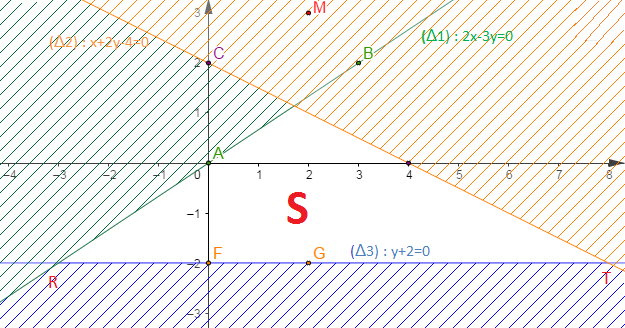
On prend $M\begin{pmatrix} 2 \\ 3 \end{pmatrix}$ comme point de vérification.
Pour $2x-3y\geq 0$, on aura $2(2)-3(3)\geq 0.$
Alors, $4-9\geq 0$, donc $-5\geq 0$ ; ce qui est impossible.
Pour $x+2y-4\leq 0$, on aura $2+2(3)-4\leq 0.$
Alors, $2+6-4\leq 0$, donc $4\leq 0$ ; ce qui est impossible.
Pour $y+2\geq 0$, on aura $3+2\geq 0.$
Alors, $5\geq 0$ ; ce qui est toujours vraie.
Ainsi, la partie triangulaire du graphique est solution du système.
Auteur:
Abdoulaye Ba

Commentaires
Sall (non vérifié)
lun, 01/07/2019 - 02:06
Permalien
Un grand merci pour le
Mor talla Cissé (non vérifié)
mar, 01/08/2019 - 23:23
Permalien
Félicitations
Anonyme (non vérifié)
mar, 03/05/2019 - 08:18
Permalien
Merci beaucoup pour votre
Anonyme (non vérifié)
mar, 03/05/2019 - 09:15
Permalien
Modou et son pere ont total
mndiaye
mar, 03/05/2019 - 14:29
Permalien
Si x est l'age de Modou et y
Si x est l'age de Modou et y l'age du père, on a x+y=50
Alae (non vérifié)
mer, 12/16/2020 - 18:32
Permalien
Si
Oury diallo (non vérifié)
lun, 02/22/2021 - 22:30
Permalien
Devenir mathématicien
Anonyme (non vérifié)
mer, 04/07/2021 - 03:01
Permalien
Un très bon document, un
Anonyme (non vérifié)
ven, 09/16/2022 - 19:46
Permalien
yo les reuf
Anonyme (non vérifié)
ven, 09/16/2022 - 19:46
Permalien
yo les reuf
Ajouter un commentaire