Bac Maths D, Union des Comores 2015

Le plan complexe est rapporté à un repère orthonormé direct $(O\ ;\ \vec{u}\ ;\ \vec{j}).$

On considère l'équation $(E)\ :\ Z_{2}+(3-\mathrm{i})Z-4(1+\mathrm{i})=0$ et la suite $\left(M_{n}\right)$ des points d'affixes $\left(Z_{n}\right)=\left(\sqrt{2}\mathrm{e}^{\mathrm{i}\dfrac{\pi}{4}}\right)$ définie pour $n\geq 1.$

1. a) Calculer $Z_{1}$ ; $Z_{2}$ ; $Z_{3}$ et $Z_{4}.$

b) Placer les points $M_{1}$ ; $M_{2}$ ; $M_{3}$ et $M_{4}.$

2. a) Vérifier que $Z_{1}$ est une solution de l'équation $(E).$

b) En déduire l'autre solution de $(E).$

3. a) Donner l'écriture complexe de la similitude directe $f$ de centre $M_{2}$ et qui transforme $M_{1}$ et $M_{3}.$

b) En déduire le rapport et l'angle de $f.$

c) Quelle est l'image de la droite $\left(M_{1}M_{2}\right)$ par $f$ ?  

4. On pose $d_{n}=\left|Z_{n}+1-Z_{n}\right|$ et $L_{n}=d_{1}+d_{2}+d_{3}+\ldots+d_{n}$ pour tout $n\geq 1.$

a) Calculer $d_{n}$ en fonction de $n.$

b) En déduire l'expression de $L_{n}$ en fonction de $n.$

c) Déterminer le plus petit entier naturel $n$ tel que $L_{n}\geq 10.$

Un touriste européen veut visiter $2$ villes de notre pays parmi $3$ : $V_{1}$ ; $V_{2}$ et $V_{3}.$

Il part de l'aéroport situé en $A.$

Les lignes représentent les routes par lesquelles il peut passer d'une ville à l'autre.

Il fait ses visites totalement au hasard, sans repasser deux fois dans la même ville déjà visitée ni revenir à l'aéroport.

Par exemple : $A-V_{2}-V_{3}$ est une liste de visite possible de deux villes.
 

 
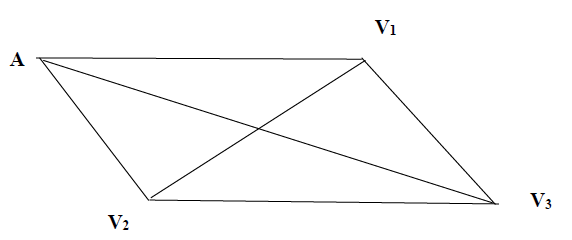
1. Indiquer toutes les listes de visite de deux villes.

2. Calculer les probabilités des évènements suivants :

$A$ : « le touriste visite la ville $V_{3}$ »  

$B$ : « le touriste visite $V_{3}$ en dernier »

$C$ : « le touriste visite $V_{3}$ avant $V_{2}$ »  

$D$ : « le touriste ne visite pas $V_{3}$ »

On suppose que tous les listes ont la même probabilité.  

3. Soit $X$ la variable aléatoire qui associe l'ordre de $V_{3}$ visitée par le touriste.  

a) Déterminer l'ensemble des valeurs prises par $X$ ; On admet que si $V_{3}$ ne figure pas dans la liste alors $X=0.$

b) Donner la loi de probabilité de $X.$

c) Calculer l'espérance mathématique de $X.$

Les parties A et B sont indépendantes

On considère la fonction $f$ définie sur $]-1\ ;\ 0[\cup ]0\ ;\ +\infty[$ par $f(x)=\ln(x+1)+\dfrac{m}{\ln(x+1)}$ où $m$ est un réel strictement positif.
 
On désigne par $(\mathcal{C})$ la courbe représentative de $f$ ; unité graphique étant égale à $2\,cm.$

1. a) Déterminer les limites de $f$ aux bornes de l'ensemble de définition de $f.$

b) Interpréter graphiquement les résultats obtenus.  

2. On suppose que $m=(\ln2)^{2}.$

a) Calculer $f'(x)$ et étudier son signe.

b) En déduire le sens de variation de $f.$

c) Dresser le tableau de variation de $f.$  

3. Tracer la courbe $(\mathcal{C}).$
 
4. On pose : $$I_{n}=\int^{3}_{1}f(x)\mathrm{d}x$$

a) Montrer que pour tout $x\in[1\ ;\ 3]\;,\ \dfrac{5}{2}\ln 2\leq f(x)\leq 3\ln 2.$

b) Donner une interprétation géométrique de $I.$

c) En déduire un encadrement de $I.$

On considère la fonction $g$ définie sur $]1\ ;\ +\infty[$ par $g(x)=\dfrac{1}{4x+\sqrt{\ln x+1}}$

Pour tout entier $n\geq 1$, on pose $$\alpha_{n}=\mathrm{e}^{n^{2}+2n}\quad\text{et}\quad \beta=\int^{\alpha_{n}}_{\alpha_{1}}g(x)\mathrm{d}x.$$

1. En remarquant que $g(x)=\dfrac{1}{4}\left(\dfrac{\dfrac{1}{x}}{\sqrt{\ln x+1}}\right)$, déterminer une primitive $G$ de $g$ sur $]1\ ;\ +\infty[.$

2. a) Calculer $\alpha_{1}$ ; $G\left(\alpha_{1}\right)$ et $G\left(\alpha_{n}\right)$

b) Exprimer $\beta_{n}$ en fonction de $n.$  

c) Montrer que $\left(\beta_{n}\right)$ est une suite arithmétique dont on précisera la raison $r$ et le premier terme $\beta_{1}.$