Vous êtes ici

Solution des exercices : Généralité sur les champs magnétique - champs magnétiques des courants - Ts

Classe:

Terminale

Exercice 1

1) Représentation du spectre de l'aimant

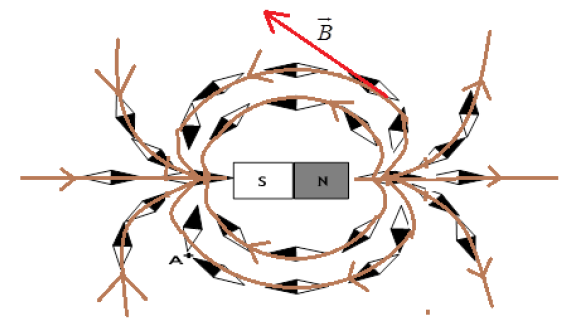
2) a) Calcul de l'intensité du champ magnétique au point

$A$

$B=\dfrac{1m\,T\times227\,mV}{20\,mV}\Rightarrow\;B=11.35\,mT$

b) Tracé le vecteur champ magnétique au point

$A.$ (Voir figure)

Exercice 2

1) Tracé du spectre de l'aimant en

$U$ entre les deux pôles

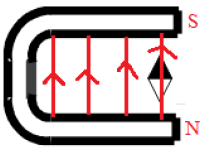
2) Orientation des lignes de champ. (Voir figure)

3) Identification des pôles de l'aimant. (Voir figure)

4) Le vecteur

$\overrightarrow{B}$ dans cette région de l'espace champ magnétique est constant.

Un tel champ magnétique est appelé champ magnétique uniforme.

Exercice 3

1) Identification des pôles du solénoïde.

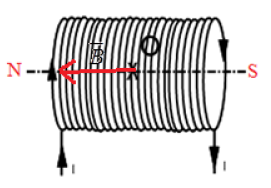
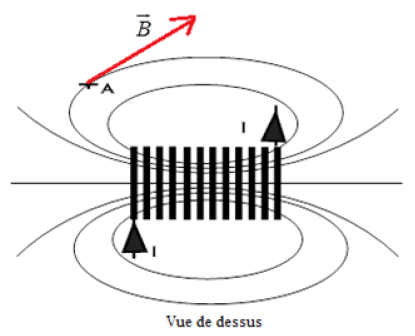
2) Calcul de la norme du champ magnétique créé au centre de ce solénoïde.

$\begin{array}{lcl} B&=&\mu_{0}\dfrac{N}{L}I\\&=&4\pi\cdot10^{-7}\dfrac{N}{L}I\\&=&4\pi\cdot110^{-7}\times\dfrac{2000}{50\cdot10^{-2}}\times1.5\\\Rightarrow B&=&7.5\cdot10^{-3}T \end{array}$

3) Représentation du vecteur champ magnétique au centre du solénoïde. (Voir figure)

4) Représentation le vecteur champ magnétique en

$A$ (Voir figure).

Exercice 4

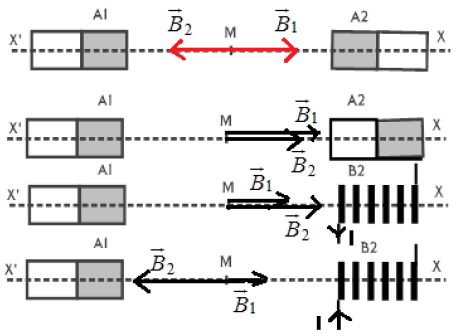
1) Représentation du vecteur champ magnétique en

$M$ , lorsque les deux pôles en regard sont de même nom.

$\overrightarrow{B}=\overrightarrow{B_{1}}+\overrightarrow{B_{2}}=\overrightarrow{0}$

2) Représentation du vecteur champ magnétique en

$M$ , lorsque les deux pôles sont de noms différents.

$\overrightarrow{B}=\overrightarrow{B_{1}}+\overrightarrow{B_{2}}$

$\overrightarrow{B_{1}}=\overrightarrow{B_{2}}\Rightarrow\;\overrightarrow{B}=2\overrightarrow{B_{1}}$ ;

$B=2\times20\Rightarrow\;B=40\,mT$

3) La norme du champ magnétique créé par la bobine

Premier cas :

$\begin{array}{lcl} \overrightarrow{B}&=&\overrightarrow{B_{1}}+\overrightarrow{B_{2}}\\\Rightarrow B&=&B_{1}+B_{2}\\\Rightarrow B_{2}&=&B-B_{1}\\&=&60-20\\\Rightarrow B_{2}&=&40\,mT \end{array}$

Deuxième cas :

$\begin{array}{lcl} \overrightarrow{B}&=&\overrightarrow{B_{1}}+\overrightarrow{B_{2}}\\\Rightarrow B&=&B_{1}-B_{2}\\\Rightarrow B_{2}&=&B+B_{1}\\&=&60+20\\\Rightarrow B_{2}&=&80\,mT \end{array}$

Sens du courant voir figure.

Exercice 5

1) Représentation des vecteurs champs magnétique créés en

$M$ par chacune des deux sources.

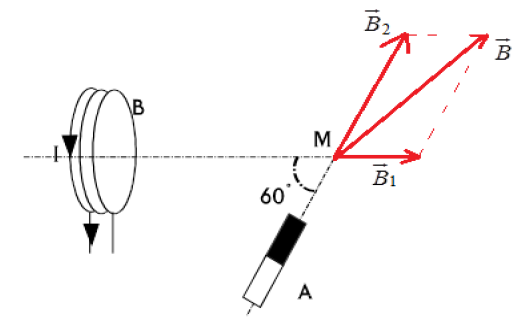
2) Représentation du vecteur champ magnétique résultant. Voir figure

Détermination de la norme du vecteur champ magnétique

$\begin{array}{lcl} \overrightarrow{B}&=&\overrightarrow{B_{1}}+\overrightarrow{B_{2}}\\\Rightarrow B^{2}&=&B_{1}^{2}+B_{2}^{2}+2B_{1}^{2}B_{2}^{2}\cos\left(\overrightarrow{B_{1}}\;,\ \overrightarrow{B_{2}}\right)\\\Rightarrow B&=&\sqrt{B_{1}^{2}+B_{2}^{2}+2B_{1}^{2}B_{2}^{2}\cos\left(\overrightarrow{B_{1}}\;,\ \overrightarrow{B_{2}}\right)}\\B&=&\sqrt{2^{2}+4^{2}+2\times 2\times 4\cos 60^{\circ}}\\\Rightarrow B&=&5.3\,mT \end{array}$

Exercice 6

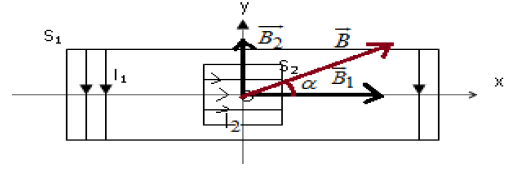
1) Représentation du vecteur induction magnétique

$B_{1}$ au centre de

$S_{1}.$ (Voir figure)

Expression de l'intensité du vecteur induction magnétique

$B_{1}$ en fonction de

$n_{1}$ et

$I_{1}.$

$B_{1}=4\pi\cdot10^{-7}n_{1}I_{1}$

2) Sens de

$I_{2}$ pour que le vecteur induction

$B_{2}$ crée au centre de

$S_{2}$ ait le même sens que l'axe

$(y'y).$ (Voir figure)

3) Une petite aiguille aimantée, placée au centre

$O$ des deux solénoïdes prend une direction

$\alpha$ avec l'axe

$(x'x).$

3) a) Schéma dans lequel sont représentés les vecteurs

$B_{1}$ ,

$B_{2}$ et l'aiguille.

b) Expression du rapport

$\dfrac{n_{2}}{n_{1}}$ en fonction de

$\alpha$ ,

$I_{1}$ et

$I_{2}.$

$\begin{array}{lcl} \tan\alpha&=&\dfrac{B_{2}}{B_{1}}\\&=&\dfrac{4\pi\cdot10^{-7}n_{2}I_{2}}{4\pi\cdot10^{-7}n_{1}I_{1}}\\\Rightarrow \dfrac{n_{2}}{n_{1}}&=&\dfrac{I_{1}}{I_{2}}\tan\alpha \end{array}$

c) Calcul de

$n_{1}$ et

$n_{2}$

$\tan\alpha=\dfrac{n_{2}I_{2}}{n_{1}I_{1}}\Rightarrow\;n_{1}=\dfrac{n_{2}I_{2}}{I_{1}\tan\alpha}$

$\begin{array}{lcl} n_{1}+n_{2}&=&500\\\Rightarrow\dfrac{n_{2}I_{2}}{I_{1}\tan\alpha}+n_{2}&=&500\\\Rightarrow\,n_{2}\left(\dfrac{I_{2}}{I_{1}\tan\alpha}+1\right)&=&500\\\Rightarrow n_{2}&=&\dfrac{500}{\dfrac{I_{2}}{I_{1}\tan\alpha}}+1\\\Rightarrow n_{2}&=&\dfrac{500}{\dfrac{1}{2\tan 63.2^{\circ}}}+1\\\Rightarrow n_{2}&=&399\,spires\cdot m^{-1}\\\Rightarrow n_{1}&=&500-399\\\Rightarrow n_{1}&=&101\,spires\cdot m^{-1} \end{array}$

Valeur du champ résultant en

$O.$

$\begin{array}{lcl} B&=&\dfrac{B_{1}}{\cos\alpha}\\&=&\dfrac{4\pi\cdot10^{-7}n_{1}I_{1}}{\cos\alpha}\\&=&\dfrac{4\pi\cdot10^{-7}\times101\times2}{\cos 63.2^{\circ}}\\\Rightarrow B&=&0.56\,mT \end{array}$

Exercice 7

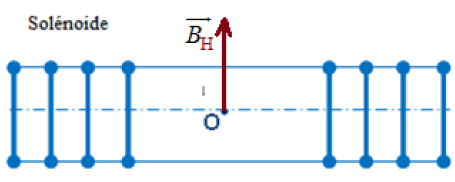
1) Représentation le vecteur

$\overrightarrow{B_{H}}$ composante horizontale du champ géomagnétique.

2) Représentation du vecteur

$\overrightarrow{B_{S}}$ du champ magnétique crée par le courant électrique

$i$ au centre

$O$ du solénoïde.

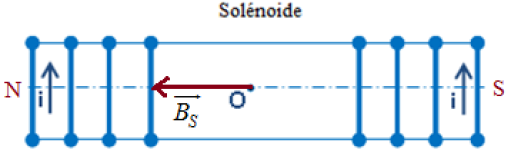
Déduction des faces nord et sud du solénoïde. (Voir figure)

3) a) Détermination de l'équation numérique de la courbe

$\tan\alpha=f(i).$

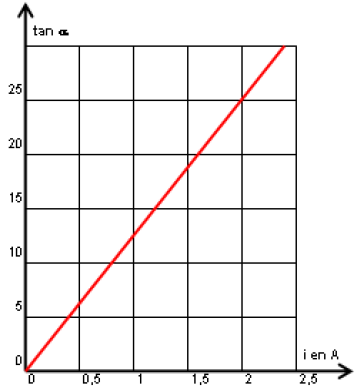
La courbe représentant

$\tan\alpha=f(i)$ est une droite qui passe par l'origine d'équation de la forme :

$\begin{array}{lcl} \tan\alpha&=&ai\\ \text{avec }a&=&\dfrac{\Delta\tan\alpha}{\Delta\,i}\\&=&\dfrac{25-0}{2-0}\\\Rightarrow a&=&12.5\\\Rightarrow\tan\alpha&=&12.5\,i \end{array}$

b) Représentation des vecteurs

$\overrightarrow{B_{H}}$ et

$\overrightarrow{B_{S}}$

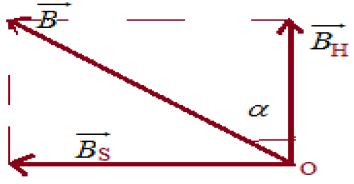
c) Relation entre la valeur de

$B_{H}$ et

$B_{S}$ et

$\alpha$

$\tan\alpha=\dfrac{B_{S}}{B_{H}}\Rightarrow\;B_{H}=\dfrac{B_{S}}{\tan\alpha}$

4) Valeur de la composante horizontale

$B_{H}$ du champ géomagnétique.

$\begin{array}{lcl} \tan\alpha&=&\dfrac{B_{S}}{B_{H}}\\\Rightarrow B_{H}&=&\dfrac{B_{S}}{\tan\alpha}\\&=&\dfrac{4\pi\cdot10^{-7}ni}{12.5i}\\&=&\dfrac{4\pi\cdot10^{-7}n}{12.5}\\&=&\dfrac{4\pi\cdot10^{-7}\times200}{12.5}\\\Rightarrow B_{H}&=&2.0\cdot10^{-5}T \end{array}$

Exercice 8

Partie I

$\begin{array}{|c|c|c|c|c|c|c|c|} \hline x(cm)&0&4&8&11&14&17&20\\ \hline B_{S}(mT)&3.3&3.3&3.3&3.3&3.2&2.8&2.1\\ \hline \end{array}$

1) Tracé les variations de

$B$ en fonction de

$x$ sur toute la longueur du solénoïde

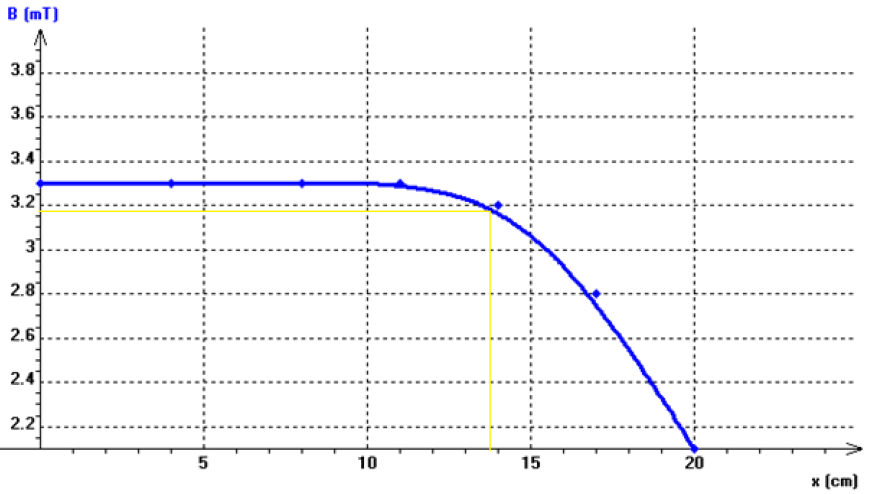
2) Le champ magnétique à l'intérieur de la bobine est uniforme.

3) Calcul de l'intensité

$I$ du courant qui traverse la bobine.

$\begin{array}{lcl} B&=&4\pi\cdot10^{-7}\dfrac{N}{L}I\\\Rightarrow I&=&\dfrac{B}{4\pi\cdot10^{-7}N}\\&=&\dfrac{3.3\cdot10^{-3}}{4\pi\cdot10^{-7}\times250}\\\Rightarrow I&=&10.5\,A \end{array}$

4) Détermination de la longueur du solénoïde sur laquelle la valeur du champ magnétique reste supérieure à

$90\%$ de sa valeur maximale

$\begin{array}{lcl} B&\geq& 90\%B_{max}\\\Rightarrow B&\geq&\dfrac{90}{100}\times 3.3\\\Rightarrow B&\geq&2.97\,mT\\\Rightarrow x&=&13.8\,cm \end{array}$

Partie II

1) Sens du courant dans les spires pour que le champ crée par la bobine soit dirigé vers la droite. (Voir figure)

2) Schéma représentant les vecteurs champs créés par le solénoïde

$\overrightarrow{B_{S}}$ ; par la Terre

$\overrightarrow{B_{H}}$ , et le champ résultant.

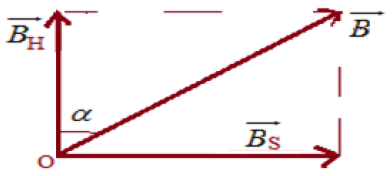
3) Calcul de la nouvelle valeur de

$B_{S}$

$\begin{array}{lcl} \tan\alpha&=&\dfrac{B_{S}}{B_{H}}\\\Rightarrow B_{S}&=&B_{H}\tan\alpha\\&=&2.0\cdot10^{-5}\times\tan 14.3^{\circ}\\\Rightarrow B_{S}&=&5.1\cdot10^{-6}T \end{array}$

Auteur:

Amary Thiam & Sidy Mouhamed Ndiaye

Commentaires

Abbou essaid (non vérifié)

ven, 03/20/2020 - 02:49