Série d'exercices : Condensateurs : capacité, énergie emmagasinée - 1er s
Classe:
Première
Exercice 1
On dispose d'un condensateur de capacité $C.$
On se propose de le charger à l'aide d'un générateur de courant constant $I=0.5mA.$
On mesure en fonction du temps la d.d.p aux bornes du condensateur et on obtient les valeurs consignées dans le tableau de mesure suivant :
$$\begin{array}{|c|c|c|c|c|c|c|c|} \hline t\text{ en }ms&0&20&40&60&80&100&120\\ \hline U\text{ en }V&0&1&2&3&4&5&6\\ \hline \end{array}$$
1) Tracer le graphe $u=f(t).$
Conclure
Échelles :
$1cm\ \rightarrow\ 20ms$
$1cm\ \rightarrow\ 1V$
2) Détermine la variation de $u$ en fonction du temps.
En déduire la capacité du condensateur
Exercice 2
1) Calculer la capacité équivalente pour chaque schéma.
Avec $C_{1}=10\mu F$, $C_{2}=2\mu F$ et $C_{2}=1000nF$
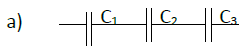
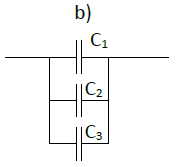
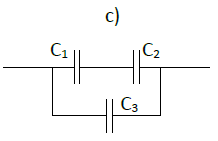
2) Déterminer la valeur de $C_{CB}$
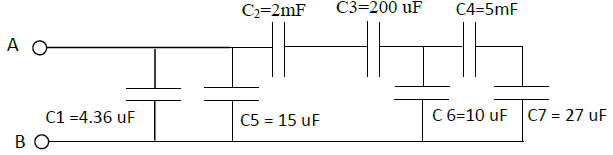
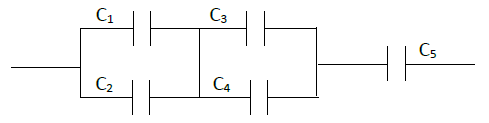
La capacité équivalente du schéma ci-dessous est de $155\,nF.$
Calculer la capacité $C_{3}$ en sachant que $C_{1}=C_{2}=100\,nF$, $C_{4}=470 \,nF$ et $C_{5}=1\mu F.$
Exercice 3
I. Les caractéristiques d'un condensateur sont les suivantes : $C=0.12\mu F$, épaisseur du diélectrique $e=0.2\,mm$ ; permittivité relative de l'isolant :
$\mathcal{E}_{r}=5$ ; tension de service : $U_{S}=100\,V.$ $\mathcal{E}_{0}= 8.84\cdot10^{-12}F/m.$
Calculer :
1) La surface des armatures.
2) La charge du condensateur soumis à la tension de service.
3) L'énergie emmagasinée dans ces conditions.
II. Le condensateur étant chargé, on l'isole, puis on l'associe en parallèle à un condensateur de capacité $C_{1}=0.15\mu F$ initialement déchargé.
Calculer :
1) La charge totale de l'ensemble formé par les deux condensateurs.
2) La tension commune aux deux condensateurs en régime permanent.
3) L'énergie emmagasinée par le montage
Exercice 4
On réalise un circuit électrique, comportant en série, un générateur idéal de courant débitant un courant d'intensité constante $I=50\mu A$, un conducteur ohmique, un interrupteur $K$, un condensateur de capacité $C$ inconnue et un voltmètre.
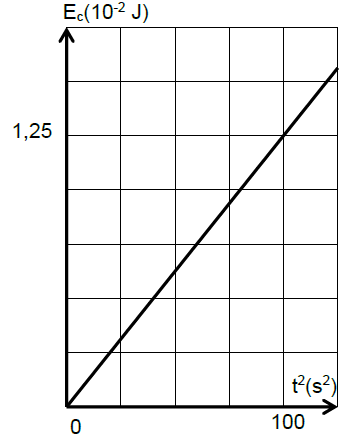
A un instant pris comme origine des dates, on ferme l'interrupteur $K$ et on suit l'évolution de la tension $u_{c}$ aux bornes du condensateur au cours du temps, ce qui a permis de tracer la courbe d'évolution de l'énergie électrique $E_{c}$ emmagasinée dans le condensateur en fonction du carré du temps.(figure 3)
1) Représenter le schéma du montage qui permet de suivre l'évolution de $u_{c}$ au cours du temps.
2) En exploitant le graphe, déterminer la capacité $C$ du condensateur.
3) Le condensateur utilisé est plan de permittivité électrique absolue $\mathcal{E}$, l'aire de la surface commune en regard est $s=1m^{2}$ et l'épaisseur du diélectrique est $e=0.1mm.$
Calculer la permittivité relative du condensateur.
On donne $\mathcal{E}_{0}=8.85\cdot10^{-12}S.I$
Exercice 5
1) On charge un condensateur par un courant constant $I_{0}=0.30\,mA$ pendant $8s.$
La tension $U$ aux bornes du condensateur est alors de $12V.$
Quelle est la capacité $C$ du condensateur en $\mu F$ ?
2) Le condensateur d'un flash électronique de capacité $150\mu F$ est chargé avec une tension $U$ de $500V.$
Quelle est la valeur de la charge $q$ portée par son armature positive ?
Quelle est l'énergie $E$ stockée par ce condensateur ?
$(E_{électrique}=1/2CU^{2})$
Exercice 6
On prend un condensateur de capacité $C_{1}=470\mu F$ et chargé avec la tension $U_{1}=24V.$
1) Calculer la valeur de l'énergie $W_{1}$ emmagasinée par $C_{1}.$
On prend un deuxième condensateur de capacité $C_{2}=1000\mu F$ déchargé $(U_{2}=0V).$
2) Quelle est la valeur de l'énergie $W_{2}$ emmagasinée par $C_{2}.$
On branche maintenant les deux condensateurs $C_{1}$ et $C_{2}$ en parallèle.
3) Déterminer la valeur de la tension $U$ aux bornes des deux condensateurs
4) Calculer la valeur de l'énergie $W_{12}$ emmagasinée par l'ensemble $C_{1}\parallel C_{2}.$
5) Comparer $W_{12}$ avec $W_{1}+W_{2}$ et donner une explication au résultat.
Exercice 7 Charge d'un condensateur à courant constant
Un condensateur de capacité $C$ inconnu est chargé à courant constant $I=250\mu A.$
A l'instant $t_{0}=0$, le condensateur est initialement déchargé.
La charge commence.
Après une durée $t_{1}=7\,min$, la tension $U$ aux bornes du condensateur est $U=31.8\,V.$
1) Rappeler l'expression de la charge $Q$ $(i\;,\ t)$ et les unités utilisées.
2) Rappeler l'expression de la tension $Q$ $(C\;,\ U)$ et les unités utilisées.
3) Déterminer la charge $Q$ portée par une armature du condensateur pour l'instant $t=t_{1}.$
4) Tracer la courbe $U(Q)$
Échelle :
$10V\ \rightarrow\ 2cm$ ;
$10\,mC\ \rightarrow\ 1\,cm.$
5) En déduire la capacité $C$ du condensateur.
6) Calculer l'énergie $W$ emmagasinée par le condensateur à la l'instant $t_{1}.$
Exercice 8 Association de condensateurs
On dispose de deux condensateurs $C_{1}=2200\mu F$ et $C_{2}=3.3\,mF.$
1) Établir l'expression de la capacité équivalente $CS$ lorsque les deux condensateurs sont branchés en série.
2) Établir l'expression de la capacité équivalente $CP$ lorsque les deux condensateurs sont branchés en parallèle.
3) On charge le condensateur $C_{1}$ sous la tension $U=30\,V.$
Déterminer la charge $Q_{1}$ portée par une armature de ce condensateur.
4) On isole le condensateur $C_{1}$ et on branche le condensateur $C_{2}$, initialement déchargé, à ses bornes.
Déterminer la charge portée par l'ensemble.
5) En déduire la tension $U'$ aux bornes de l'ensemble.
Exercice 9 Association de condensateurs en parallèle
1. Un condensateur de $C_{1}=6\mu F$ est branché en parallèle avec un condensateur de $C_{2}=10\,mF.$
La charge accumulée sur les armatures du groupe de condensateurs est de $200\,mC.$
1.1 Quelle est la capacité équivalente du groupe de deux condensateurs ?
1.2 Quelle est la d.d.p. aux bornes des condensateurs en parallèle ?
1.3 Quelle est la charge accumulée sur les armatures du condensateur de $6\,mF$ ?
1.4 Quelle est la charge accumulée sur les armatures du condensateur de $10\,mF$ ?
2. Un condensateur $C_{1}=3.3\,mF$ est chargé sous la tension $U=20\,V$, un autre condensateur $C_{2}=2200\mu F$ est chargé sous la tension $U'=10\,V.$
2.1 Déterminer pour charge condensateur les charges $Q_{1}$ et $Q_{2}.$
2.2 Les deux condensateurs sont isolés et branchés en dérivation.
Quelle est alors la charge $Q$ portée par l'ensemble ?
2.3 En déduire la tension $U''$ aux bornes de l'ensemble
Exercice 10 Association de condensateurs en série
Deux condensateurs, initialement déchargés, de capacité $C_{1}=20\,nF$ et $C_{2}=33\,nF$ sont branchés en série.
L'ensemble est alimenté sous la tension $U=20\,V.$
1) Déterminer la capacité équivalente $C_{EQ}.$
2) Calculer la charge $Q$ portée par la capacité équivalente.
3) Quelle est la charge $q$ portée par un condensateur.
4) En déduire la tension $U_{1}$ aux bornes de $C_{1}$ et $U_{2}$ aux bornes de $C_{2}.$
5) Calculer l'énergie $W$ emmagasinée par l'ensemble.
Exercice 11
Un condensateur a ses deux plaques $A$ et $B$ verticales, distantes de $d=0.10\,m.$
On applique la tension constante $U_{AB}=4\cdot10^{4}V.$
Les plaques sont percées aux point $A'$ et $B'$ situés sur une même horizontale perpendiculaire aux plaques.
L'ensemble est placé dans le vide.
Des ions Zinc $II$, $Zn^{2+}$, de masse $m=1.16\cdot10^{-25}Kg$ pénètrent en $A'$ avec une vitesse $V_{A'}=105m/s.$
La charge élémentaire est $e=1.6\cdot10^{-19}C.$
1. Quelles sont les caractéristiques de la force électrique $\overrightarrow{F}$ qui s'exerce sur chaque ion entre les deux plaques $A$ et $B$ ?
2. Évaluer le rapport $\dfrac{P}{F}$, en désignant par $P$ le poids d'un ion.
Conclure. $g=10m\cdot s^{-2}.$
3. Calculer l'énergie cinétique de chaque ion arrivant en $B'$, en Joules et en électronvolts :
3.1 En utilisant le théorème de l'énergie cinétique.
3.2 En utilisant la conservation de l'énergie totale $(E_{c}+E_{p})$ ou $E_{p}$ est l'énergie potentielle électrique de l'ion, la position de référence étant l'ion en $B'.$
3.3 En déduire la vitesse d'un ion en $B'.$
Exercice 12
1) Un condensateur de capacité $C_{1}=2\mu F$, chargé à l'aide d'un générateur de $f.é.m.$ $E=6V$ et de résistance interne négligeable, est isolé du générateur de charge.
a) Quelle est la tension entre ses bornes à la fin de la charge ?
b) Quelle est l'énergie emmagasinée par ce condensateur ?
2) Le condensateur $C_{1}$ est alors relié à un deuxième condensateur de capacité $C_{2}=1\mu F$ non chargé.
Le condensateur $C_{1}$ se décharge partiellement dans $C_{2}.$
a) Quand est ce que le courant s'annule dans le circuit formé par $C_{1}$ et $C_{2}$ ?
b) Calculer les charges électriques finales de chacun de deux condensateurs.
c) Quelle est l'énergie emmagasinée par chaque condensateur $C_{1}$ et $C_{2}$ ainsi chargés ?
3) Quelle est la capacité du condensateur équivalent à l'association de condensateurs $C_{1}$ et $C_{2}$ dans chacun des cas suivants :
a) Les condensateurs $C_{1}$ et $C_{2}$ sont branchés en série ?
b) Les condensateurs $C_{1}$ et $C_{2}$ sont branchés en parallèle ?

Commentaires
Oumar (non vérifié)
sam, 10/03/2020 - 19:15
Permalien
Élève
Bassirou (non vérifié)
ven, 02/24/2023 - 10:50
Permalien
Je veux être avec vous
Farah (non vérifié)
mar, 11/19/2024 - 13:45
Permalien
Condensateur
Unaul KENZO (non vérifié)
lun, 12/07/2020 - 03:48
Permalien
Félicitations
Anonyme (non vérifié)
ven, 06/18/2021 - 08:23
Permalien
le corrigé du exo9 s'il vous
Jules12 (non vérifié)
sam, 04/30/2022 - 01:48
Permalien
Aide
Beni Joël (non vérifié)
ven, 05/20/2022 - 18:03
Permalien
Corrigé de l'exercice 2
Faure Eude (non vérifié)
dim, 01/15/2023 - 05:17
Permalien
Exercices corrigées
NOURI (non vérifié)
sam, 04/15/2023 - 17:45
Permalien
NASSIMA
Abdou kader Gaye (non vérifié)
lun, 04/08/2024 - 13:18
Permalien
Suggestion
Ajouter un commentaire