Révisions de trigonométrie -T S
Classe:
Terminale
Formules fondamentales
1) Dans les tableaux ci-dessous, on récapitule les propriétés des fonctions trigonométriques.
(On pourra les retrouver à l'aide d'un cercle trigonométrique).
$$\begin{array}{|l|} \hline \cos^{2}x+\sin^{2}x=1\\ \hline \tan x=\dfrac{\sin x}{\cos x}\\ \hline \text{co}\tan x=\dfrac{\cos x}{\sin x}\\ \hline \end{array}\qquad\begin{array}{|l|} \hline 1+\tan^{2}x=\dfrac{1}{\cos^{2}x}\\ \hline 1+co\tan^{2}x=\dfrac{1}{\sin^{2}x}\\ \hline \end{array}$$
$$\begin{array}{|c|c|c|c|c|c|} \hline x&0&\dfrac{\pi}{6}&\dfrac{\pi}{4}&\dfrac{\pi}{3}&\dfrac{\pi}{2}\\ \hline \cos x&1&\dfrac{\sqrt{3}}{2}&\dfrac{\sqrt{2}}{2}&\dfrac{1}{2}&0\\ \hline \sin x&0&\dfrac{1}{2}&\dfrac{\sqrt{2}}{2}&\dfrac{\sqrt{3}}{2}&1\\ \hline \tan x&0&\dfrac{1}{\sqrt{3}}&1&\sqrt{3}&\text{Non définie}\\ \hline \end{array}\qquad\begin{array}{|c|c|c|c|c|c|c|} \hline x&x+2\pi&-x&x+\pi&\pi-x&x+\dfrac{\pi}{2}&\dfrac{\pi}{2}-x\\ \hline \cos x&\cos x&\cos x&-\cos x&-\cos x&-\sin x&\sin x\\ \hline \sin x&\sin x&-\sin x&-\sin x&\sin x&\cos x&\cos x\\ \hline \tan x&\tan x&-\tan x&\tan x&-\tan x&-co\tan x&co\tan x\\ \hline \end{array}$$
$$\begin{array}{|l|} \hline \sin x=\sin a\text{ si et seulement si :}\\ x=a+2k\pi\text{ ou }x=\pi-a+2k\pi\ (k\in\mathbb{Z})\\ \hline \cos x=\cos a\text{ si et seulement si :}\\ x=a+2k\pi\text{ ou }x=\pi-a+2k\pi\ (k\in\mathbb{Z})\\ \hline \tan x=\tan a\text{ si et seulement si :}\\ x=a+k\pi\ (k\in\mathbb{Z})\\ \hline \end{array}$$
$$\begin{array}{|l|} \hline \cos(x+y)=\cos x\cos y-\sin x\sin y\\ \hline \sin(x+y)=\sin x\cos y+\cos x\sin y\\ \hline \cos(x-y)=\cos x\cos y+\sin x\sin y\\ \hline \sin(x-y)=\sin x\cos y-\cos x\sin y\\ \hline \tan(x+y)=\dfrac{\tan x+\tan y}{1-\tan x\tan y}\\ \hline \tan(x-y)=\dfrac{\tan x-\tan y}{1+\tan x\tan y}\\ \hline \end{array}\qquad\begin{array}{|l|} \hline (1)\quad\cos 2x=\cos^{2}x-\sin^{2}x\\ \hline (2)\quad\cos 2x=2\cos^{2}x-1\\ \hline (3)\quad\cos 2x=1-2\sin^{2}x\\ \hline \sin 2x=2\sin x\cos x\\ \hline \tan 2x=\dfrac{2\tan x}{1-\tan x\tan y}\\ \hline \end{array}$$
2) On pose :
$\tan\dfrac{x}{2}=t.$
Exprimer en fonction de $t$ :
$\cos x$, $\sin x$ et $\tan x.$
Si $\tan\dfrac{x}{2}=t$, on a :
$$\begin{array}{|c|c|c|} \hline \cos x=\dfrac{1-t^{2}}{1+t^{2}}&\sin x=\dfrac{2t}{1+t^{2}}&\tan x=\dfrac{2t}{1-t^{2}}\\ \hline \end{array}$$
3) Formules de linéarisation et de factorisation :
a) En utilisant les résultats rappelés dans les tableaux précédents, compléter en fonction de :
$\cos(a-b)$, $\sin(a-b)$, $\cos(a+b)$ et $\sin(a+b)$, le premier tableau ci-dessous.
b) En posant :
$p=a+b$ et $q=a-b$, déduire du premier tableau les formules du deuxième tableau.
$$\begin{array}{|c|} \hline \sin a\cdot\cos b=\dfrac{1}{2}[\sin(a+b)+\sin(a-b)]\\ \hline \cos a\cdot\cos b=\dfrac{1}{2}[\cos(a+b)+\cos(a-b)]\\ \hline \sin a\cdot\sin b=\dfrac{1}{2}[\cos(a-b)-\cos(a+b)]\\ \hline \end{array}\qquad\begin{array}{|c|} \hline \sin p+\sin q=2\sin\dfrac{p+q}{2}\cos\dfrac{p-q}{2}\\ \hline \sin p-\sin q=2\cos\dfrac{p+q}{2}\sin\dfrac{p-q}{2}\\ \hline \cos p+\cos q=2\cos\dfrac{p+q}{2}\cos\dfrac{p-q}{2}\\ \hline \cos p-\cos q=-2\sin\dfrac{p+q}{2}\sin\dfrac{p-q}{2}\\ \hline \end{array}$$
4) Études des fonctions trigonométriques :
a) Dans les tableaux ci-dessous, rappeler la parité, la périodicité et la dérivabilité des fonctions trigonométriques ainsi que l'expression de leur fonction dérivée :
$$\begin{array}{|c|c|c|c|c|c|c|} \hline &\text{définie sur}&\text{dérivable sur}&\text{parité}&\text{période}&\text{à étudier sur}&\text{fonction dérivée}\\ \hline f(x)=\sin x&\mathbb{R}&\mathbb{R}&\text{impaire}&2\pi&[0\;;\ \pi]&f'(x)=\cos x\\ \hline g(x)=\cos x&\mathbb{R}&\mathbb{R}&\text{paire}&2\pi&[0\;;\ \pi]&f'(x)=\cos x\\ \hline h(x)=\tan x&\mathbb{R}\setminus\left\{(2k+1)\dfrac{\pi}{2}\;,\ k\in\mathbb{Z}\right\}&\mathbb{R}\setminus\left\{(2k+1)\dfrac{\pi}{2}\;,\ k\in\mathbb{Z}\right\}&\text{impaire}&\pi&\left[0\;;\ \dfrac{\pi }{2}\right[&f'(x)=\dfrac{1}{\cos^{2}x}=1+\tan^{2}x\\ \hline\end{array}$$
b) Courbes
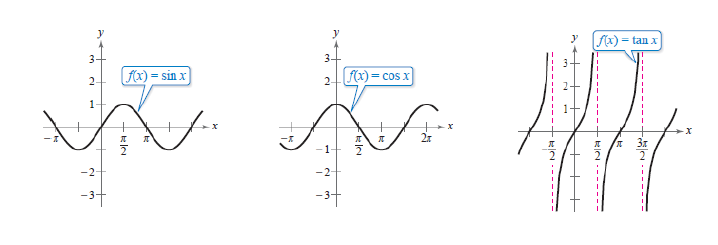
Auteur:
Mouhamadou ka

Commentaires
Abdelkader (non vérifié)
dim, 11/29/2020 - 12:15
Permalien
merci pour votre aide à tous
ali (non vérifié)
lun, 12/20/2021 - 08:29
Permalien
Merci pour ces documents
Assane Ndiaye (non vérifié)
mar, 04/25/2023 - 20:39
Permalien
Téléchargements pour mes élèves
Assane Ndiaye (non vérifié)
mar, 04/25/2023 - 20:39
Permalien
Téléchargements pour mes élèves
Anonyme (non vérifié)
jeu, 02/22/2024 - 10:50
Permalien
Tuu
Anonyme (non vérifié)
ven, 07/19/2024 - 02:44
Permalien
Très intéressant
Anonyme (non vérifié)
mer, 09/17/2025 - 12:11
Permalien
Merci beaucoup
Ajouter un commentaire