Vous êtes ici

Bac Physique chimie 1er groupe S2 S2A S4 S5 2006

Exercice 1 (04 points)

Le transfert d'information lors de la communication entre les insectes, se fait par signaux chimiques entre individus, d'espèces différentes ou de même espèce au moyen d'une substance (ou un mélange de substances) appelée phéromone.

Ce phénomène est très courant chez les êtres vivants.

Un individu $a$ secrète en quantité très faible de la phéromone à l'extérieur ; celle-ci est perçue par un individu $b$ de la même espèce chez lequel elle provoque une réaction comportementale spécifique, voire une modification physiologique.

Le mot phéromone vient des mots grecs pherein (=transporter) et hormân (=exciter)

Certaines phéromones sont des signaux d'alarmes, d'autres permettent le marquage d'une piste, enfin certaines (attractives ou aphrodisiaques) attirent les insectes de sexe opposé en vue de la reproduction.

Voici quelques exemples de phéromones :

- Phéromone d'alarme de l'abeille :

molécule $A$ : $C_{7}H_{14}O_{2}$

- Phéromone de piste de fourmi coupeuse de feuille : Atta Texana

molécule $B$ : $C_{7}H_{9}O_{2}N$

- Phéromone sexuelle d'un insecte nuisible pour les conifères :

molécule $C$ : $C_{8}H_{16}O$

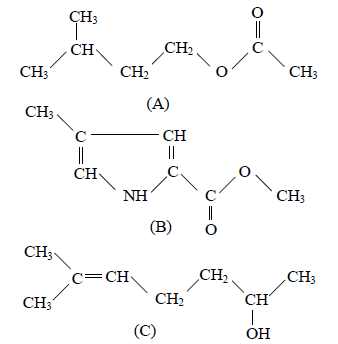
1.1 Reproduire sur la copie les molécules $A$ et $C.$

Entourer et nommer les groupes caractéristiques présents. (0.5 point)

1.2 La phéromone d'alarme $A$ peut être synthétisée à partir d'un acide carboxylique et d'un alcool.

1.2.1 Écrire les formules semi développées de l'acide et de l'alcool dont dérive $A.$

Les nommer. (0.5 point)

1.2.2 Écrire l'équation de la réaction associée à la transformation chimique de synthèse de la phéromone $A.$

Comment nomme-t-on cette transformation ?

Préciser ses caractéristiques. (0.75 point)

1.2.3 Avec quel catalyseur pourrait-on réaliser cette transformation chimique ? (0.25 point)

1.3 A partir de quels dérivés d'acide carboxylique peut-on synthétiser $A$ avec le même alcool ?

Indiquer les effets de ce changement de réactifs sur la transformation. (0.5 point)

1.4 On fait réagir une solution d'hydroxyde de sodium avec la phéromone $B.$

Cette phéromone sera notée $R-COOCH_{3}.$

Comment appelle-t-on cette transformation ?

Préciser ses caractéristiques. (0.5 point)

1.5 Une solution de la molécule $C$ de concentration massique $10^{-15}g\cdot L^{-1}$ (appelée aussi sulcatrol car libérée par le Gnatotricus sulcatus) peut être utilisée par l'homme pour protéger les cultures des insectes nuisibles en les attirant soit loin des cultures que l'on veut protéger soit vers des pièges très sélectifs.

1.5.1 Quels avantages de cette solution de phéromone peut-on tirer dans l'agriculture comparativement aux insecticides classiques ? (0.75 point)

1.5.2 Calculer la concentration molaire volumique de cette solution. (0.25 point)

Masses molaires atomiques :

$M(C)=12g\cdot mol^{-1}$ ;

$M(H)=1g\cdot mol^{-1}$ ;

$M(O)=16g\cdot mol^{-1}$

Exercice 2 (04 points)

2.1 On fabrique $100\,mL$ d'une solution d'acide chlorhydrique $0.05\,mol\cdot L^{-1}$ par dilution d'un volume $V_{1}$ de solution chlorhydrique de concentration molaire $1\,mol\cdot L^{-1}.$

Déterminer le volume $V_{1}$, et expliquer brièvement comment on réalise pratiquement cette opération. (0.5 point)

2.2 La solution d'acide chlorhydrique $0.05\,mol\cdot L^{-1}$ est ajoutée progressivement à $20\,mL$ d'une solution aqueuse de monoéthylamine $(C_{2}H_{5}NH_{2})$ dans le but de doser celle-ci.

Un pH-mètre permet de suivre l'évolution du pH du mélange au cours de cette manipulation.

Les résultats obtenus sont consignés dans le tableau ci-après où $V_{a}$ représente le volume d'acide versé :

$$\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|} \hline V_{a}\;(mL)&0&5&10&15&20&25&30&35&36&38&40&43&45&50\\ \hline pH&11.8&11.4&11.1&10.9&10.7&10.5&10.2&9.8&9.7&9.3&6.1&2.7&2.4&2.1\\ \hline \end{array}$$

2.2.1 Écrire l'équation de la réaction de dosage. (0.25 point)

2.2.2 Tracer la courbe $pH=f(V_{a}).$

On prendra comme échelles : en abscisses $1\,cm$ pour $4\,mL$, en ordonnées $1\,cm$ pour une unité de $pH.$ (0.75 point)

2.2.3 Déterminer les coordonnées du point équivalent par une méthode que l'on précisera (0.25 point)

2.2.4 En déduire :

a) La concentration molaire $C_{b}$ de la solution de monoéthylamine. (0.25 point)

b) Le pKa du couple associé à la monéthhylamine. (0.25 point)

2.3 Calculer les concentrations molaires volumiques des espèces présentes dans le mélange lorsque le volume d'acide versé est de $30\,mL.$

Retrouver la valeur du pKa à l'aide des valeurs trouvées. (0.5 point)

2.4 On désire préparer une solution tampon.

2.4.1 Qu'est ce qu'une solution tampon ?

Quelles sont ses propriétés caractéristiques ? (0.5 point)

2.4.2 Préciser la manière d'obtenir $100\,mL$ d'une solution tampon à partir de la solution de monoéthylamine précédente et de la solution d'acide chlorhydrique $0.05\,mol\cdot L^{-1}.$ (0.75 point)

Exercice 3 (04 points)

On considère un dipôle $(D)$ de nature inconnue monté en série avec un conducteur ohmique de résistance $R=100\,W$ et un générateur basse fréquence de tension sinusoïdale dont la fréquence et la tension efficace sont réglables.

On utilise un oscillographe dont les réglages sont les suivants : balayage horizontal $(5\cdot 10^{-2}ms/\text{div})$, déviation verticale (pour la voie $1$ : $0.5\,V/\text{div}$ ; pour la voie $2$ : $1\,V/\text{div})$

On reproduit une photographie de l'écran lorsque l'oscillographe est branché selon le schéma ci-dessous.

(voir figures $1$ et $2$)

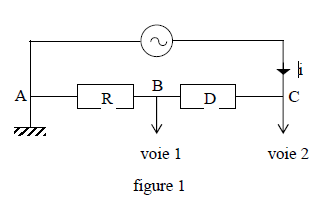
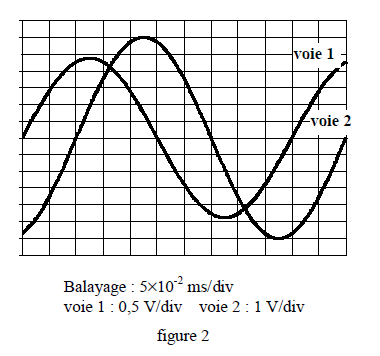
3.1 En déduire :

3.1.1 la fréquence de la tension sinusoïdale ; (0.25 point)

3.1.2 les valeurs efficaces de l'intensité instantanée $i(t)$ qui traverse le circuit et de la tension instantanée $u_{CA}(t)$ aux bornes du générateur ; (0.5 point)

3.1.3 le déphasage $\phi$ de la tension $u_{CA}(t)$ par rapport à l'intensité $i(t).$

Préciser s'il y'a avance ou retard de $u_{CA}(t)$ par rapport à $i(t).$ (0.75 point)

3.1.4 On envisage pour $(D)$ certaines hypothèses :

$(D)$ est un conducteur ohmique,

$(D)$ est une bobine de résistance $r$ et d'auto inductance $L$,

$(D)$ est un condensateur,

$(D)$ est une bobine de résistance $r$ et d'auto inductance $L$ en série avec un condensateur de capacité $C.$

Sans calcul et en justifiant les réponses, éliminer les hypothèses non vraisemblables. (0.75 point)

3.2 La tension aux bornes du générateur étant maintenue constante à la valeur $U_{0}=12V$, on fait varier la fréquence et on relève à chaque fois la valeur de l'intensité efficace.

Pour une fréquence $N_{0}=2150\,Hz$, on constate que l'intensité efficace passe par un maximum de valeur $I_{0}=107\,mA.$

3.2.1 Quelle est la nature du dipôle $(D)$ ?

Justifier la réponse. (0.5 point)

3.2.2 En déduire toutes les valeurs numériques qui le caractérisent. (01.25 point)

Exercice 4 (04 points)

4.1 Dans la théorie de Bohr de l'atome d'hydrogène, les énergies des différents niveaux sont données par la formule :

$E_{n}=-\dfrac{13.6}{n^{2}}$ (en eV) ; $n$ est un nombre entier positif

Le spectre d'émission de l'atome d'hydrogène contient les trois raies visibles :

(orangée) : $\lambda_{1}=656.3\,nm$ ;

(bleue) : $\lambda_{2}=486.1\,nm$ ;

(indigo) : $\lambda_{3}=434.1\,nm.$

On donne les niveaux d'énergie de l'atome d'hydrogène dans le diagramme énergétique simplifié ci-dessous :

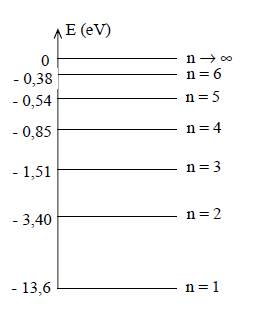
4.1.1 Quel est le niveau correspondant à l'état fondamental ? (0.25 point)

4.1.2 Calculer, en $eV$, l'énergie d'un photon des radiations lumineuses de longueur d'onde $\lambda_{1}$, $\lambda_{2}$, $\lambda_{3}.$ (0.5 point)

4.1.3 Montrer que chacune de ces trois raies correspond à une transition d'un niveau excité, que l'on précisera, au niveau $n=2.$ (0.75 point)

4.1.4 Quelle est l'énergie d'ionisation de l'atome d'hydrogène ? (0.5 point)

Quelle est la longueur d'onde correspondant à l'ionisation de l'atome d'hydrogène (pris à l'état fondamental) ? (0.25 point)

4.2 Une source de lumière composée de ces trois radiations $\lambda_{1}$, $\lambda_{2}$, $\lambda_{3}$ est utilisée pour éclairer une cellule photoélectrique au potassium.

L'énergie d'extraction d'un électron du métal potassium est $W_{0}=2.2\,eV.$

A l'aide de filtres appropriés on peut isoler chacune des radiations précédentes pour étudier leur effet.

4.2.1 Quelles sont parmi ces trois radiations celles qui provoquent une émission d'électrons ?

Justifier la réponse. (0.75 point)

4.2.2 Calculer la vitesse maximale d'émission des électrons pour chacun des cas où l'émission est possible. (01 point)

Données numériques :

$1\,eV=1.6\cdot 10^{-19}J$ ;

constante de Planck : $h=6.62\cdot 10^{-34}J\cdot s$

célérité de la lumière dans le vide : $c=3\cdot 10^{8}m\cdot s^{-1}$ ;

masse de l'électron : $m=9.1\cdot10^{-31} kg$ ;

charge élémentaire : $e=1.6\cdot 10^{-19}C.$

Exercice 5 (04 points)

Dans tout le problème, on supposera que le mouvement des ions a lieu dans le vide et que leur poids est négligeable

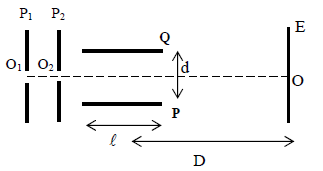
5.1 Des ions $Mg^{2+}$, sortant d'une chambre d'ionisation, pénètrent, avec une vitesse négligeable, par un trou

$O_{1}$, dans l'espace compris entre deux plaques verticales $P_{1}$ et $P_{2}.$

Lorsqu'on applique entre ces deux plaques une tension $U_{0}$, les ions atteignent le trou $O_{2}$ avec la vitesse $\overrightarrow{v}_{0}$

5.1.1 Quelle plaque $(P_{1}\text{ ou }P_{2})$ doit-on porter au potentiel le plus élevé ? Pourquoi ? (0.25 point)

5.1.2 Donner la valeur de $v_{0}$ en fonction de la charge $q$, de la masse $m$ d'un ion et de $U_{0}.$ (0.25 point)

5.1.3 Calculer la valeur de $v_{0}$ pour les ions $_{12}^{24}Mg^{2+}$ dans le cas où $U_{0}=4000\,V.$

On prendra :

$m\left(_{12}^{24}Mg^{2+}\right)=24\,u$ ;

$u=1.67\cdot 10^{-27}Kg$ ;

$e=1.60\cdot 10^{-19}C.$ (0.25 point)

5.2 A la sortie de $O_{2}$, les ions ayant cette vitesse $\overrightarrow{v}_{0}$ horizontale pénètrent entre les armatures $P$ et $Q$ d'un condensateur.

On applique entre ces armatures une différence de potentiel positive $U_{PQ}$ que l'on notera $U$, créant entre elles un champ électrique uniforme vertical.

5.2.1 Préciser les caractéristiques de la force électrique à laquelle chaque ion est soumis, on exprimera son intensité en fonction de $q$, $U$ et de la distance $d$ entre les plaques $P$ et $Q.$ (0.5 point)

5.2.2 Déterminer la nature de la trajectoire d'un ion à l'intérieur de ce condensateur lorsque $U$ garde une valeur constante. (0.75 point)

5.2.3 On dispose d'un écran vertical $E$ à la distance $D$ du centre des plaques de longueur $\ell$, trouver en fonction de $q$, $m$, $U$, $v_{0}$, $\ell$, $D$ et $d$ l'expression de la distance $z=OM$, $M$ étant le point d'impact d'un ion sur l'écran.

La distance $OM$ dépendra t-elle des caractéristiques des ions positifs utilisés ?

(On admet que la tangente à la trajectoire au point de sortie $S$ du condensateur passe par le milieu de celui-ci) (0.75 point)

5.2.4 Calculer la durée de la traversée du condensateur dans le cas où $\ell=10\,cm.$ (0.5 point)

5.2.5 On applique entre $P$ et $Q$ une tension sinusoïdale $u=U_{max}\cdot\sin\omega\,t$, de fréquence $f=50\,Hz.$

Montrer qu'avec un pinceau d'ions, on obtient sur l'écran $E$ un segment de droite verticale, dont on calculera la longueur dans le cas où $U_{max}=230\,V$, $D=40\,cm$, $d=4\,cm.$

(On peut considérer que, durant toute la traversée du condensateur, chaque ion est soumis à une tension presque constante). (0.75 point)