Vous êtes ici

Solution des exercices : Statistiques - 4e

Classe:

Quatrième

Exercice 1

Dans chacun des cas suivants, précisons : La population étudiée ; le caractère étudié et la nature du caractère.

$1e$ cas : Le principal du collège relève le niveau des élèves de son établissement.

$-\$ La population étudiée est l'ensemble des élèves de l'établissement

$-\$ Le caractère étudié est le niveau des élèves

$-\$ Ce caractère est de nature qualitative

$2e$ cas : Docteur Gueye de l'hôpital Ousmane NGOM de Saint-Louis relève le groupe sanguin de ces

$25$ patients.

$-\$ La population étudiée est l'ensemble des

$25$ patients

$-\$ Le caractère étudié est le groupe sanguin

$-\$ Ce caractère est de nature qualitative

Exercice 2

Lors d'un stage, Mme Tall a mesuré la taille des jeunes majorettes du collège. Elle a obtenu les résultats en

$cm\ :$

$\begin{array}{ccccccccccccc} 160&170&173&160&175&185&175&180&170&173&185&175&180 \\175&170&180&175&173&180&185&160&173&175&180&175& \\ \end{array}$

1) La population étudiée est constituée des jeunes majorettes du collège.

Son effectif est égal à

$25.$

2) Le caractère étudié est la taille.

Ce caractère est de nature quantitative.

3) Recopions et complétons le tableau suivant.

$\begin{array}{|l|c|c|c|c|c|c|c|}\hline\text{Modalités}&160&170&173&175&180&185&\text{Total} \\ \hline\text{Effectifs}&3&3&4&7&5&3&25\\ \hline\text{Fréquences }\%&12&12&16&28&20&12&100\\ \hline\end{array}$

4) a) Le mode de cette série est la modalité

$175$

En effet, on sait que le mode d'un caractère est la modalité qui a l'effectif le plus élevé. C'est aussi la valeur qui a la plus grande fréquence.

Or, on constate que la modalité

$175$ a l'effectif le plus élevé

$7$ ou encore la fréquence la plus grande fréquence

$28\%.$

Par conséquent, la modalité

$175$ représente le mode de la série.

b) Calculons la taille moyenne.

Soient :

$\centerdot\ \ x_{1}\;,\ x_{2}\;,\ x_{3}\;,\ x_{4}\;,\ x_{5}\$ et

$\ x_{6}$ les modalités de la série

$\centerdot\ \ n_{1}\;,\ n_{2}\;,\ n_{3}\;,\ n_{4}\;,\ n_{5}\$ et

$\ n_{6}$ leurs effectifs respectifs et

$N$ l'effectif total.

Alors, la moyenne

$\bar{x}$ de cette série statistique est donnée par :

$\bar{x}=\dfrac{1}{N}\sum_{i=1}^{6}n_{i}\times x_{i}$

Par suite,

$\begin{array}{rcl} \bar{x}&=&\dfrac{n_{1}\times x_{1}+n_{2}\times x_{2}+n_{3}\times x_{3}+n_{4}\times x_{4}+n_{5}\times x_{5}+n_{6}\times x_{6}}{N}\\ \\&=&\dfrac{3\times 160+3\times 170+4\times 173+7\times 175+5\times 180+3\times 185}{25}\\\\&=&\dfrac{480+510+692+1225+900+555}{25}\\\\&=&\dfrac{4362}{25}\\\\&=&174.48\end{array}$

Donc,

$\boxed{\bar{x}=174.48\;cm}$

Ainsi, la taille moyenne est égale à

$174.48\;cm$

5) Représentons les diagrammes : en bâtons et circulaire des effectifs.

$-\$ Diagramme en bâtons

Pour cela, on choisit une échelle et on met en ordonnée les effectifs partiels, en abscisse les modalités et on trace les diagrammes en bâtons.

Soit alors, en ordonnée :

$1\;cm$ pour une

$(1)$ jeune majorette

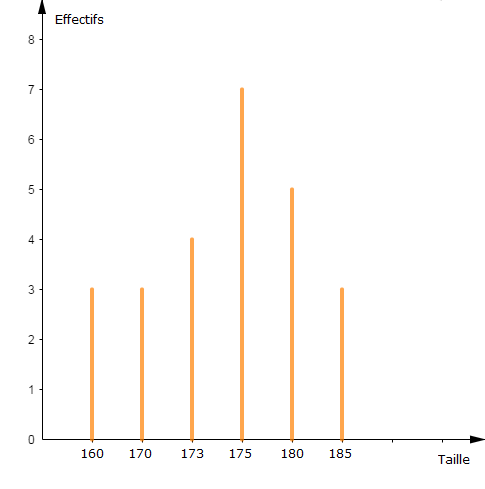
$\text{Diagramme en bâtons}$

$-\$ Diagramme circulaire

Pour réaliser ce diagramme, on affecte à chaque modalité un angle

$\alpha^{\circ}$ correspondant.

On a :

$360^{o}$ correspond à

$N$ (effectif total) et

$\alpha^{o}$ correspond à

$n$ (effectif partiel)

Ainsi,

$\alpha^{o}=\dfrac{360^{o}\times n}{N}$

Donc, pour chaque effectif partiel d'une modalité, on applique cette formule pour déterminer l'angle correspondant.

Les résultats sont alors donnés dans le tableau ci-dessous

$\begin{array}{|l|c|c|c|c|c|c|c|}\hline\text{Modalités}&160&170&173&175&180&185&\text{Total}\\ \hline\text{Effectifs}&3&3&4&7&5&3&25\\ \hline\alpha^{\circ}&43.2&43.2&57.6&100.8&72&43.2&360\\ \hline\end{array}$

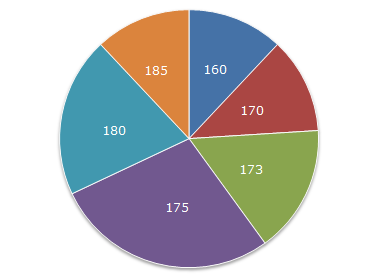
$\text{Diagramme circulaire}$

Exercice 3

On considère les deux séries de notes.

$\text{Série 1 : } 10\;;\ 13\;;\ x\;;\ 14\;;\ 12\;;\ 7.$

$\text{Série 2 : } 9\;;\ 7\;;\ 11\;;\ x\;;\ 13\;;\ 15\;;\ 12.$

Déterminons

$x$ pour que les deux séries aient la même moyenne.

Soit

$N_{1}=6$ l'effectif total de la série

$1\$ et

$\ N_{2}=7$ l'effectif total de la série

$2.$

Notons

$m_{1}$ la moyenne de la série

$1\$ et

$\ m_{2}$ la moyenne de la série

$2.$

Alors, on a :

$\begin{array}{rcl} m_{1}&=&\dfrac{10+13+x+14+12+7}{6}\\ \\&=&\dfrac{56+x}{6}\end{array}$

Donc,

$\boxed{m_{1}=\dfrac{56+x}{6}}$

$\begin{array}{rcl} m_{2}&=&\dfrac{9+7+11+x+13+15+12}{7}\\ \\&=&\dfrac{67+x}{7}\end{array}$

Donc,

$\boxed{m_{2}=\dfrac{67+x}{7}}$

Ainsi, les deux série ont la même moyenne si, et seulement si,

$m_{1}=m_{2}$

Ce qui signifie :

$\dfrac{56+x}{6}=\dfrac{67+x}{7}$

En résolvant cette équation, on trouve alors la valeur de

$x$ vérifiant l'égalité des deux moyennes.

Soit alors :

$\begin{array}{rcl} \dfrac{56+x}{6}=\dfrac{67+x}{7}&\Leftrightarrow&7\times(56+x)=6\times(67+x)\\ \\&\Leftrightarrow&7\times 56+7\times x=6\times 67+6\times x\\\\&\Leftrightarrow&392+7x=402+6x\\\\&\Leftrightarrow&7x-6x=402-392\\\\&\Leftrightarrow&x=10\end{array}$

Donc,

$\boxed{x=10}$

Ainsi, pour que les deux séries aient la même moyenne,

$x$ doit prendre la valeur

$10.$

Auteur:

Diny Faye