Vous êtes ici

Corrigé BFEM Maths 2019

Exercice 1

1) Pour rappel, la médiane d'une série statistique à caractère quantitatif est la valeur de la série qui partage l'effectif total en deux groupes de même effectif.

Pour obtenir la valeur de la médiane d'une série statistique ordonnée à caractère quantitatif discret et d'effectif total $N$, on procède comme suit :

$-\ $ On regarde d'abord si l'effectif total $N$ est pair ou impair.

$-\ $ Si $N$ est impair alors, on considère $\dfrac{N+1}{2}$

Donc, la $\left(\dfrac{N+1}{2}\right)^{\text{ième}}$ valeur de la série correspond à la valeur de la médiane.

Ainsi,

$$V_{_{\text{médiane}}}=V_{_{\frac{N+1}{2}}}$$

$-\ $ Si $N$ est pair alors, on considère $\dfrac{N}{2}$ et la valeur de la médiane se trouve entre la $\left(\dfrac{N}{2}\right)^{\text{ième}}$ et la $\left(\dfrac{N}{2}+1\right)^{\text{ième}}$ valeur de la série.

Donc, la valeur de la médiane est égale à la somme des valeurs qui correspondent à ces rangs, divisée par deux.

Ainsi,

$$V_{_{\text{médiane}}}=\dfrac{V_{_{\frac{N}{2}}}+V_{_{\frac{N}{2}+1}}}{2}$$

2) Le tableau ci-dessous donne la répartition des salaires mensuels en $\text{F CFA}$ et leurs proportions pour le personnel d'une entreprise.

$$\begin{array}{|l|c|c|} \hline \text{fonctions}&\text{Fréquences en }\%&\text{salaires}\\ \hline \text{Cadres supérieurs}&5&450 000\\ \hline \text{Agents de production}&45&350000\\ \hline \text{Personnels administratifs}&15&200000\\ \hline \text{Chauffeurs}&5&150000\\ \hline \text{Agents de sécurité}&10&100000\\ \hline \text{Agents commerciaux}&20&175000\\ \hline \end{array}$$

a) Le caractère étudié est le salaire mensuel.

Le salaire mensuel étant une grandeur mesurable donc, ce caractère est de nature quantitative.

b) Calculons le salaire moyen mensuel dans cette entreprise.

Soit $S_{_{M}}$ le salaire moyen mensuel et soient :

$\ast\ \ S_{1}\;,\ S_{2}\;,\ S_{3}\;,\ S_{4}\;,\ S_{5}$ et $\ S_{6}$ les salaires mensuels respectifs du personnel selon la fonction.

$\ast\ \ n_{1}\;,\ n_{2}\;,\ n_{3}\;,\ n_{4}\;,\ n_{5}$ et $\ n_{6}$ les effectifs partiels respectifs et $N$ l'effectif total.

$\ast\ \ f_{1}\;,\ f_{2}\;,\ f_{3}\;,\ f_{4}\;,\ f_{5}$ et $\ f_{6}$ les fréquences respectives

Alors, on a :

$\begin{array}{rcl} S_{_{M}}&=&\dfrac{n_{1}\times S_{1}+n_{2}\times S_{2}+n_{3}\times S_{3}+n_{4}\times S_{4}+n_{5}\times S_{5}+n_{6}\times S_{6}}{N}\\ \\&=&\dfrac{n_{1}}{N}S_{1}+\dfrac{n_{2}}{N}S_{2}+\dfrac{n_{3}}{N}S_{3}+\dfrac{n_{4}}{N}S_{4}+\dfrac{n_{5}}{N}S_{5}+\dfrac{n_{6}}{N}S_{6}\\ \\&=&f_{1}S_{1}+f_{2}S_{2}+f_{3}S_{3}+f_{4}S_{4}+f_{5}S_{5}+f_{9}S_{6}\end{array}$

Donc,

$\begin{array}{rcl} S_{_{M}}&=&0.20\times 175000+0.1\times 100000+0.05\times 150000+0.15\times 200000+0.45\times 350000+0.05\times 450000\\\\&=&262500\end{array}$

Ainsi, le salaire moyen mensuel dans cette entreprise est de $262500\;\text{F CFA}$

3) Calculons le salaire médian de cette entreprise.

Soit $S_{_{m}}$ le salaire médian de cette entreprise.

Déterminons d'abord l'effectif total de cette entreprise.

Comme il y a exactement $2$ cadres qui travaillent dans cette entreprise alors, en utilisant la fréquence de cette catégorie de fonction, on obtient l'effectif total $N$ de cette entreprise.

Soit : $f_{6}=\dfrac{n_{6}}{N}\ $ or, $f_{6}=0.05\ $ et $\ n_{6}=2$

Donc, $\dfrac{2}{N}=0.05$, ce qui donne $N\times 0.05=2$

Par suite, $N=\dfrac{2}{0.05}=40$

Ainsi, cette entreprise compte 40 travailleurs.

40 étant un nombre pair alors, $\dfrac{40}{2}=20$

Donc, d'après la question 1), le salaire médian sera donné par :

$$S_{_{m}}=\dfrac{S_{_{20}}'+S_{_{21}}'}{2}$$

où, $S_{_{20}}'$ est le salaire du 20e travailleur et $S_{_{21}}'$ le salaire du 21e travailleur dans l'ordre croissant des salaire.

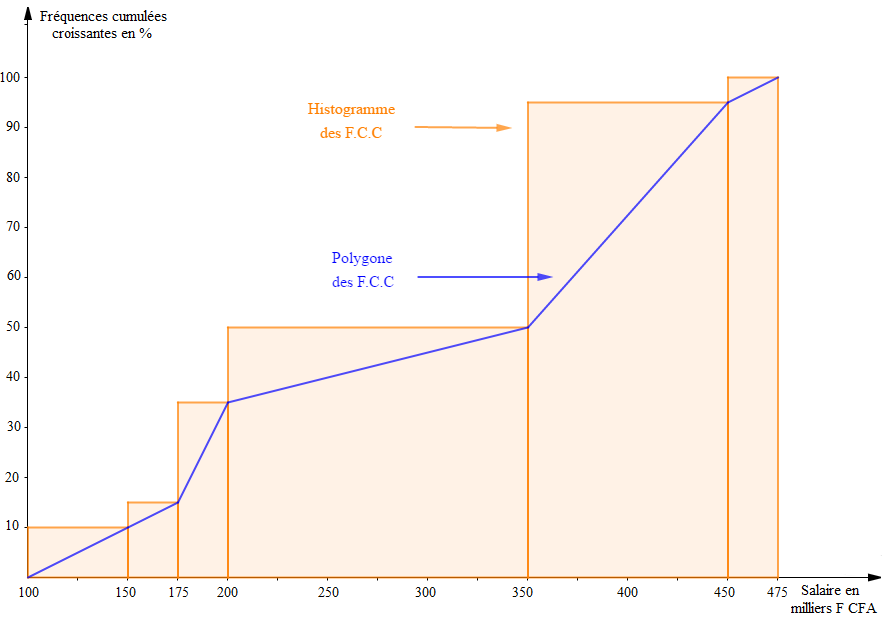
En ajoutant dans le tableau la ligne des $F.C.C$ et en réordonnant suivant l'ordre croissant des salaires (en partant du bas), on obtient :

$$\begin{array}{|l|c|c|c|} \hline \text{fonctions}&F\text{ en }\%&F.C.C\text{ en }\%&\text{salaires}\\ \hline \text{Cadres supérieurs}&5&100&450 000\\ \hline \text{Agents de production}&45&95&350000\\ \hline \text{Personnels administratifs}&15&50&200000\\ \hline\text{Agents commerciaux}&20&35&175000\\ \hline\text{Chauffeurs}&5&15&150000\\ \hline\text{Agents de sécurité}&10&10&100000\\ \hline \end{array}$$

D'après la ligne des $F.C.C\;,\ 50\%$ correspond à la moitié de l'effectif total donc,
$$S_{_{20}}'=200000\;\text{F CFA}\ \text{ et }\ S_{_{21}}'=350000\;\text{F CFA}$$

Par suite, $S_{_{m}}=\dfrac{200000+350000}{2}=275000$

Par conséquent, le salaire médian de cette entreprise est de $275000\;\text{F CFA}$

Ainsi :

$\ast\ $ 20 travailleurs ont un salaire inférieur à $275000\;\text{F CFA}$

$\ast\ $ 20 travailleurs ont un salaire supérieur à $275000\;\text{F CFA}$

4) Construisons le diagramme des fréquences cumulées croissantes de cette série.

On prendra comme échelle :

$$\begin{array}{rcl} 1\;cm&\longrightarrow&25000\text{ F CFA}\\1\;cm&\longrightarrow&10\%\end{array}$$

Exercice 2

Soit $ABCD$ un rectangle tel que $AB=12\;cm\ $ et $\ BC=x\;cm\ $ avec $\ 0<x<12.$

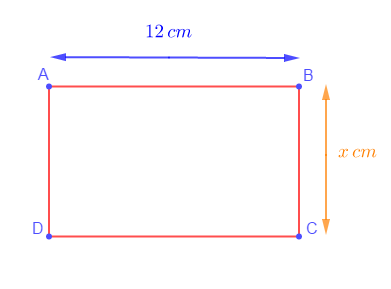
1) Calculons le périmètre $P$ du rectangle en fonction de $x.$

On sait que :

$$\text{Périmètre du rectangle}=2\times(\text{Longueur}+\text{Largeur})$$

Or, pour le rectangle $ABCD$, on a :

$$L=AB=12\;cm\ \text{ et }\ \ell=BC=x\;cm$$

Donc, $P=2\times(12+x)=2x+24$

D'où, $\boxed{P=(2x+24)\;cm}$

2) Déterminons l'intervalle dans lequel il faut choisir $x$ pour que $P$ soit supérieur à $33\;cm$

D'après la question 1), on a : $P=(2x+24)\;cm$

Donc, $P$ est supérieur à $33\;cm$ si, et seulement si,

$$2x+24>33$$

En résolvant cette inéquation, on trouvera l'intervalle de $x$

On a :

$\begin{array}{rcrcl} P>33&\Rightarrow&2x+24&>&33\\\\&\Rightarrow&2x&>&33-24\\\\&\Rightarrow&2x&>&9\\\\&\Rightarrow&x&>&\dfrac{9}{2}\end{array}$

Donc : lorsque $x$ est supérieur à $\dfrac{9}{2}=4.5\;cm$ alors, le périmètre $P$ sera supérieur à $33\;cm$

Ce qui peut s'écrire : si $x\in\left]\dfrac{9}{2}\;,\ 12\right[$ alors, $P>33\;cm$

Ainsi, l'intervalle de $x$ est

$$I=\left]\dfrac{9}{2}\;,\ 12\right[$$

3) Calculons l'aire $\mathcal{A}$ de la surface de ce rectangle en fonction de $x.$

l'aire d'un rectangle est donnée par :

$$\text{Aire du rectangle}=\text{Longueur}\times\text{Largeur}$$

Donc, $\mathcal{A}=L\times\ell$ avec, $L=12\;cm\ $ et $\ \ell=x\;cm$

Par suite, $\mathcal{A}=12\times x$

D'où, $\boxed{\mathcal{A}=12x\;cm^{2}}$

4) Déterminons l'intervalle dans lequel il faut choisir $x$ pour que $\mathcal{A}$ soit inférieure à $81\,cm^{2}$

Comme $\mathcal{A}=12x\;cm^{2}$ alors, l'aire $\mathcal{A}$ est inférieure à $81\;cm^{2}$ si, et seulement si, $12x<81$

La solution de cette inéquation donne l'intervalle de $x$, sachant que $x$ est positif car $x$ représente la largeur qui est une distance.

On a :

$\begin{array}{rcrcl}\mathcal{A}<81&\Rightarrow&12x&<&81\\ \\&\Rightarrow&x&<&\dfrac{81}{12}\\ \\&\Rightarrow&x&<&\dfrac{3\times 27}{3\times 4}\\ \\&\Rightarrow&x&<&\dfrac{27}{4}\end{array}$

Donc : lorsque $x$ est inférieur à $\dfrac{27}{4}=6.75\;cm$ alors, l'aire $\mathcal{A}$ sera inférieure à $81\;cm^{2}$

Ce qui peut encore s'écrire : si $x\in\left]0\;,\ \dfrac{27}{4}\right[$ alors, $\mathcal{A}<81\;cm^{2}$

Ainsi, l'intervalle de $x$ est

$$J=\left]0\;,\ \dfrac{27}{4}\right[$$

5) On donne $x=9\ $ et $\ A'B'C'D'$ un carré dont l'aire est égale à celle du rectangle $ABCD.$

a) Calculons le côté du carré.

On a :

$$\text{Aire du carré}=\text{côté}\times\text{côté}$$

Soit $y$ le côté du carré $A'B'C'D'$ alors, $\mathcal{A}_{(A'B'C'D')}=y\times y=y^{2}$

On a : $\mathcal{A}_{(ABCD)}=12x\;cm^{2}\ $ or, $x=9$

Donc, $\mathcal{A}_{(ABCD)}=12\times 9=108\;cm^{2}$

Ainsi, l'aire du carré est à l'aire du rectangle si, et seulement si,

$$y^{2}=108$$

En résolvant cette équation, on trouvera la mesure du côté du carré $A'B'C'D'$

On a :

$\begin{array}{rcl}\mathcal{A}_{(A'B'C'D')}=\mathcal{A}_{(ABCD)}&\Rightarrow&y^{2}=108\\ \\&\Rightarrow&y=\sqrt{108}\ \text{ ou }\ y=-\sqrt{108}\\ \\&\Rightarrow&y=6\sqrt{3}\ \text{ ou }\ y=-6\sqrt{3}\end{array}$

On prendra la valeur positive car, le côté du carré est une longueur donc, toujours positive.

Ainsi, $\boxed{\text{côté}=6\sqrt{3}\;cm}$

b) Comparons le périmètre $P$ du rectangle et celui $P'$ du carré.

On a :

$\begin{array}{rcl} P&=&2x+24\\\\&=&2\times 9+24\\\\&=&18+24\\\\&=&42\end{array}$

Donc, $P=42\;cm$

$\begin{array}{rcl} P'&=&4\times\text{côté}\\\\&=&4\times 6\sqrt{3}\\\\&=&24\sqrt{3}\end{array}$

Donc, $P'=24\sqrt{3}\;cm$

Ainsi, comparer $P\ $ et $\ P'$ revient à comparer $42\ $ et $\ 24\sqrt{3}$

Pour cela, on compare leur carré car, $42\ $ et $\ 24\sqrt{3}$ sont tous les deux positifs.

On a : $(42)^{2}=1764\ $ et $\ (24\sqrt{3})^{2}=(24)^{2}\times 3=1728$

Comme $1764$ est supérieur à $1728$ alors, $42$ est supérieur à $24\sqrt{3}$

D'où, $P>P'$

Exercice 3

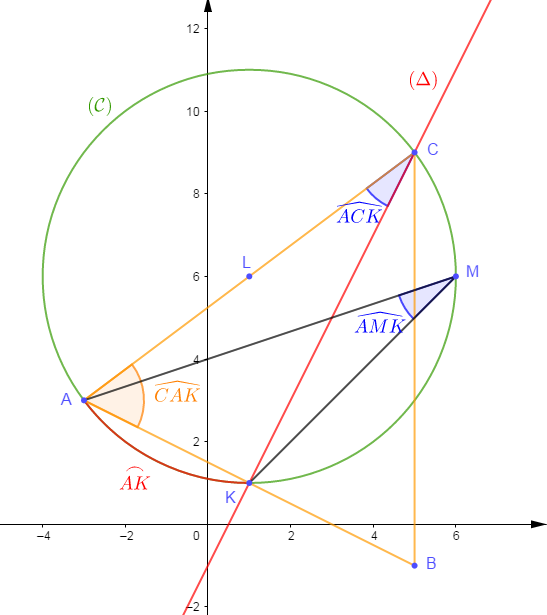
Le plan est muni d'un repère orthonormal $(O\;;\ \vec{i}\;;\ \vec{j}).$

1) Plaçons les points $A(-3\;;\ 3)\;,\ B(5\;;\ -1)\ $ et $\ C(5\;;\ 9).$

2) Trouvons une équation de la droite $(\Delta)$ hauteur du triangle $ABC$ passant par le point $C.$

$(\Delta)$ est le hauteur du triangle $ABC$ passant par le point $C$ donc, $(\Delta)$ est perpendiculaire au côté opposé à $\widehat{C}.$

C'est-à-dire : $(\Delta)\perp(AB)$

Soit $M\begin{pmatrix} x\\y\end{pmatrix}$ un point de $(\Delta).$

Comme $(\Delta)$ passe aussi par $C$ et $(\Delta)\perp(AB)$ alors, $\overrightarrow{CM}\perp\overrightarrow{AB}$ avec :

$$\overrightarrow{CM}\begin{pmatrix} x-5\\y-9\end{pmatrix}\ \text{ et }\ \overrightarrow{AB}\begin{pmatrix} 5-(-3)\\-1-3\end{pmatrix}=\begin{pmatrix} 8\\-4\end{pmatrix}$$

En appliquant la propriété sur l'orthogonalité de deux vecteurs, on obtient :

$\begin{array}{rcrcl}\overrightarrow{CM}\perp\overrightarrow{AB}&\Leftrightarrow&(x-5)\times 8+(y-9)\times(-4)&=&0\\\\&\Leftrightarrow&8x-40-4y+36&=&0\\\\&\Leftrightarrow&8x-4y-4&=&0\\\\&\Leftrightarrow&4(2x-y-1)&=&0\\\\&\Leftrightarrow&2x-y-1&=&0\end{array}$

D'où, $\boxed{(\Delta)\ :\ 2x-y-1=0}$

Soit le point $K$ milieu de $[BA].$

a) Vérifions que $K$ appartient à $(\Delta).$

Cherchons d'abord les coordonnées de $K$

$K$ milieu du segment $[BA]$ alors, ses coordonnées seront données par :

$K\begin{pmatrix}\dfrac{x_{B}+x_{A}}{2}\\ \\\dfrac{y_{B}+y_{A}}{2}\end{pmatrix}=\begin{pmatrix}\dfrac{5-3}{2}\\ \\\dfrac{-1+3}{2}\end{pmatrix}=\begin{pmatrix}\dfrac{2}{2}\\ \\\dfrac{2}{2}\end{pmatrix}=\begin{pmatrix} 1\\1\end{pmatrix}$

Donc, $K\begin{pmatrix} 1\\1\end{pmatrix}$

$K$ appartient à $(\Delta)$ si les coordonnées de $K$ vérifient l'équation de la droite $(\Delta).$

En remplaçant les coordonnées de $K$ dans l'équation de $(\Delta)$, on obtient :

$2\times 1-1-1=2-2=0$ donc, les coordonnées de $K$ vérifient bien l'équation de $(\Delta).$

Ce qui veut dire que $K$ appartient à $(\Delta).$

b) Déduisons-en la nature du triangle $ABC$ et celle du triangle $AKC.$

$(\Delta)$ est la hauteur issue de $C$ et $(\Delta)$ passe par $K$ milieu de $[BA]$ donc, $(\Delta)$ est aussi médiatrice de $[BA].$

D'où, $ABC$ est un triangle isocèle et $AKC$ un triangle rectangle en $K.$

3) Soit $(\mathcal{C})$ le cercle circonscrit au triangle $AKC.$

a) Déterminons les cordonnées de son centre $L$ et calculons son rayon $R.$

Le triangle $AKC$ étant rectangle en $K$ alors, le cercle circonscrit à ce triangle aura pour centre le milieu de l'hypoténuse du triangle.

Donc, $L$ est milieu de $[AC]$

Ses coordonnées seront alors données par :

$L\begin{pmatrix}\dfrac{x_{A}+x_{C}}{2}\\ \\\dfrac{y_{A}+y_{C}}{2}\end{pmatrix}=\begin{pmatrix}\dfrac{-3+5}{2}\\ \\\dfrac{3+9}{2}\end{pmatrix}=\begin{pmatrix}\dfrac{2}{2}\\ \\\dfrac{12}{2}\end{pmatrix}=\begin{pmatrix} 1\\6\end{pmatrix}$

D'où, $L\begin{pmatrix} 1\\6\end{pmatrix}$

Pour déterminer son rayon, on peut calculer la distance $LA$

On a :

$\begin{array}{rcl} LA&=&\sqrt{(x_{A}-x_{L})^{2}+(y_{A}-y_{L})^{2}}\\\\&=&\sqrt{(-3-1)^{2}+(3-6)^{2}}\\\\&=&\sqrt{(-4)^{2}+(-3)^{2}}\\\\&=&\sqrt{16+9}\\\\&=&\sqrt{25}\\\\&=&5\end{array}$

Ainsi, $\boxed{R=5}$

b) Montrons que $M(6\;;\ 6)$ appartient au cercle $(\mathcal{C})$

Pour cela, on doit montrer que la distance entre le point $M$ et le centre $L$ du cercle $(\mathcal{C})$ est égale au rayon $R.$

Ce qui revient donc à montrer que $LM=5$

On a :

$\begin{array}{rcl} LM&=&\sqrt{(x_{M}-x_{L})^{2}+(y_{M}-y_{L})^{2}}\\\\&=&\sqrt{(6-1)^{2}+(6-6)^{2}}\\\\&=&\sqrt{(5)^{2}+(0)^{2}}\\\\&=&\sqrt{5^{2}}\\\\&=&|5|\\\\&=&5\end{array}$

Donc, on remarque que $LM=5$

Ce qui montre que $M$ appartient au cercle $(\mathcal{C}).$

c) Justifions que $\widehat{AMK}\ $ et $\ \widehat{ACK}$ ont la même mesure.

$\widehat{AMK}\ $ et $\ \widehat{ACK}$ sont deux angles inscrits dans $(\mathcal{C})$ et interceptant le même arc $\overset{\displaystyle\frown}{AK}.$

Donc, ils ont la même mesure.

D'où, $mes\,\widehat{AMK}=mes\,\widehat{ACK}$

d) Montrons que $\widehat{CAK}\ $ et $\ \widehat{AMK}$ sont complémentaires.

Le triangle $ACK$ étant rectangle en $K$ alors, ses deux angles aigus $\widehat{CAK}\ $ et $\ \widehat{ACK}$ sont complémentaires.

Donc, $mes\,\widehat{CAK}+mes\,\widehat{ACK}=90^{\circ}$

Or, d'après la question précédente, $mes\,\widehat{AMK}=mes\,\widehat{ACK}$

Par suite, $mes\,\widehat{CAK}+mes\,\widehat{AMK}=90^{\circ}$

D'où, $\widehat{CAK}\ $ et $\ \widehat{AMK}$ sont complémentaires.

Exercice 4

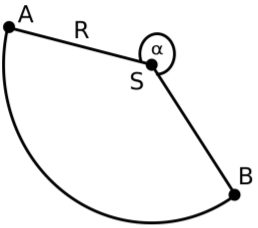
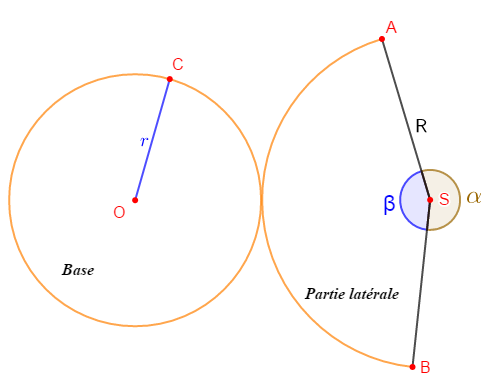
1) Le schéma ci-dessous représente le patron de la partie latérale d'un cône de révolution.

Justifions que le rayon $r$ de la base du cône vaut

$$r=R\times\left(1-\dfrac{\alpha}{360^{\circ}}\right)$$

On reprend le schéma en ajoutant le patron de la base.

On constate alors que la longueur de l'arc $\overset{\displaystyle\frown}{AB}$ est égale au périmètre de la base du cône.

Or, la longueur de l'arc $\overset{\displaystyle\frown}{AB}$ est donnée par :

$$\overset{\displaystyle\frown}{AB}=R\times\beta$$

Il faut remarquer que :

$$\beta=360^{\circ}-\alpha$$

Donc,

$$\overset{\displaystyle\frown}{AB}=R(360^{\circ}-\alpha)$$

Le périmètre de la base du cône est donné par :

$$P=r\times 360^{\circ}$$

Ainsi, on a :

$\begin{array}{rcl} P=\overset{\displaystyle\frown}{AB}&\Rightarrow&r\times 360^{\circ}=R(360^{\circ}-\alpha)\\ \\&\Rightarrow&r=\dfrac{R(360^{\circ}-\alpha)}{360^{\circ}}\\ \\&\Rightarrow&r=R\left(\dfrac{360^{\circ}-\alpha}{360^{\circ}}\right)\\ \\&\Rightarrow&r=R\left(\dfrac{360^{\circ}}{360^{\circ}}-\dfrac{\alpha}{360^{\circ}}\right)\\ \\&\Rightarrow&r=R\left(1-\dfrac{\alpha}{360^{\circ}}\right)\end{array}$

D'où, $\boxed{r=R\times\left(1-\dfrac{\alpha}{360^{\circ}}\right)}$

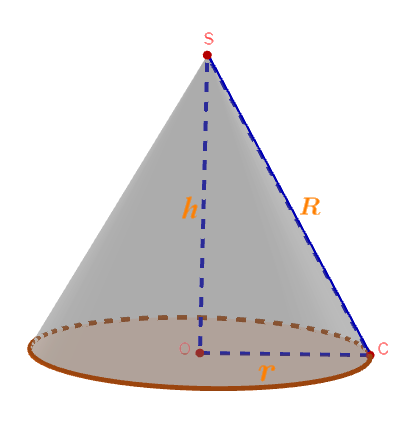
2) Démontrons que la hauteur $h$ du cône vaut :

$$h=R\times\sqrt{1-\left(1-\dfrac{\alpha}{360^{\circ}}\right)^{2}}$$

En considérant la figure ci-dessous, on constate que le triangle $COS$ est rectangle en $O.$

Donc, en appliquant le théorème de Pythagore, on obtient :

$$OS^{2}+OC^{2}=CS^{2}$$

En remplaçant $OS\;,\ OC\ $ et $\ CS$ par leur mesure respective, on trouve :

$$h^{2}+r^{2}=R^{2}$$

Ce qui donne :

$$h^{2}=R^{2}-r^{2}$$

Or, d'après la question 1), on a : $r=R\times\left(1-\dfrac{\alpha}{360^{\circ}}\right)$

Donc, en remplaçant, on obtient :

$$h^{2}=R^{2}-\left(R\times\left(1-\dfrac{\alpha}{360^{\circ}}\right)\right)^{2}$$

Par suite,

$\begin{array}{rcl} h^{2}=R^{2}-R^{2}\times\left(1-\dfrac{\alpha}{360^{\circ}}\right)^{2}&\Rightarrow&h^{2}=R^{2}\left(1-\left(1-\dfrac{\alpha}{360^{\circ}}\right)^{2}\right)\\ \\&\Rightarrow&h=\sqrt{R^{2}\left(1-\left(1-\dfrac{\alpha}{360^{\circ}}\right)^{2}\right)}\\ \\&\Rightarrow&h=\sqrt{R^{2}}\times\sqrt{1-\left(1-\dfrac{\alpha}{360^{\circ}}\right)^{2}}\\ \\&\Rightarrow&h=R\times\sqrt{1-\left(1-\dfrac{\alpha}{360^{\circ}}\right)^{2}}\end{array}$

D'où, $\boxed{h=R\times\sqrt{1-\left(1-\dfrac{\alpha}{360^{\circ}}\right)^{2}}}$

3) Exprimons l'aire du cône en fonction de $R\ $ et $\ \alpha.$

Soit $\mathcal{A}$ l'aire du cône alors, on a :

$$\mathcal{A}=\mathcal{A}_{_{L}}+\mathcal{A}_{_{B}}$$

avec, $\mathcal{A}_{_{L}}$ l'aire latérale et $\mathcal{A}_{_{B}}$ l'aire de base.

On a :

$\ast\ \ \mathcal{A}_{_{L}}=\pi\times R\times r$

Or, $r=R\times\left(1-\dfrac{\alpha}{360^{\circ}}\right)=R\times\left(1-\dfrac{\alpha}{2\pi}\right)\ $ car, pour rappel : $360^{\circ}=2\pi\;rad$

Donc, en remplaçant, on obtient :

$\boxed{\mathcal{A}_{_{L}}=\pi\times R^{2}\times\left(1-\dfrac{\alpha}{2\pi}\right)}$

$\ast\ \ \mathcal{A}_{_{B}}=\pi\times r^{2}$ avec, $r=R\times\left(1-\dfrac{\alpha}{2\pi}\right)$

Donc, en remplaçant $r$ par son expression, on obtient :

$\begin{array}{rcl}\mathcal{A}_{_{B}}&=&\pi\times r^{2}\\ \\&=&\pi\left(R\times\left(1-\dfrac{\alpha}{2\pi}\right)\right)^{2}\\ \\&=&\pi\times R^{2}\times\left(1-\dfrac{\alpha}{2\pi}\right)^{2}\end{array}$

Ainsi, $\boxed{\mathcal{A}_{_{B}}=\pi\times R^{2}\times\left(1-\dfrac{\alpha}{2\pi}\right)^{2}}$

Par suite,

$\begin{array}{rcl}\mathcal{A}&=&\mathcal{A}_{_{L}}+\mathcal{A}_{_{B}}\\ \\&=&\pi\times R^{2}\times\left(1-\dfrac{\alpha}{2\pi}\right)+\pi\times R^{2}\times\left(1-\dfrac{\alpha}{2\pi}\right)^{2}\\ \\&=&\left(\pi\times R^{2}\times\left(1-\dfrac{\alpha}{2\pi}\right)\right)\left(1+1-\dfrac{\alpha}{2\pi}\right)\\ \\&=&\pi\times R^{2}\times\left(1-\dfrac{\alpha}{2\pi}\right)\left(2-\dfrac{\alpha}{2\pi}\right)\end{array}$

D'où, $\boxed{\mathcal{A}=\pi\times R^{2}\times\left(1-\dfrac{\alpha}{2\pi}\right)\left(2-\dfrac{\alpha}{2\pi}\right)}$

4) On pose $\alpha=270^{\circ}\;,\ R=50\,cm\ $ et $\ \pi\backsimeq 3.14.$

Calculons l'aire latérale du cône.

On a :

$\begin{array}{rcl}\mathcal{A}_{_{L}}&=&\pi\times R^{2}\times\left(1-\dfrac{\alpha}{2\pi}\right)\\ \\&=&3.14\times(50)^{2}\times\left(1-\dfrac{270}{360}\right)\\ \\&=&3.14\times 2500\times\left(1-0.75\right)\\ \\&=&7850\times 0.25\\ \\&=&1962.5\end{array}$

D'où, $\boxed{\mathcal{A}_{_{L}}=1962.5\;cm^{2}}$

Auteur:

Diny Faye